Зростання і знання: три фактори доходу

У підпункті 6.2.1 була розглянута модель з двома секторами економіки: традиційним і виробляють людський капітал (сфера освіти). Тут також розглядається двухсекторной модель з традиційним сектором, але в другому секторі виробляються знання в широкому сенсі: наукові, технічні, художні. Важлива відмінність накопичених знань від кваліфікації працівників полягає в тому, що вони не розподіляються між секторами, а використовуються ними цілком, оскільки є суспільним благом.

Передбачається, що капітал і праця розподілені між двома секторами економіки у фіксованій пропорції: а_ку a_L - питомі ваги капіталу і праці в другому секторі.

Перший сектор - традиційний, він виробляє ВВП, або дохід (У), використовуючи фізичний капітал, некваліфіковану (простий) праця і накопичені знання (Л), які тут характеризують ефективність праці:

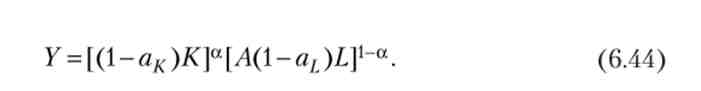
Другий сектор - виробництво знань (наука, освіта, мистецтво і ін.), Його випуск дорівнює річному приросту обсягу знань (Л). Виробнича функція залежить від капіталу, праці та накопичених знань:

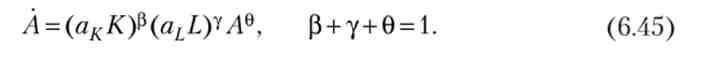
Темп приросту населення (праці) дорівнює п, приріст капіталу становить фіксовану частку доходу:

де s - норма заощадження (амортизації немає).

Стаціонарний зростання - темпи зростання капіталу (g_K) і знань (g_A) постійні.

Крива незмінного темпу зростання капіталу - безліч точок в площині (g_A, g_K), для яких темп зростання капіталу залишається незмінною.

Підставами (6.44) в (6.46) і отримаємо формулу приросту капіталу. Розділимо її на обсяг капіталу, отримаємо формулу темпу приросту капіталу. Прологаріфміруем і продифференцируем її, отримаємо формулу темпу приросту показника g_K. Прирівняємо нулю її праву частину, отримаємо формулу кривої незмінного темпу зростання капіталу:

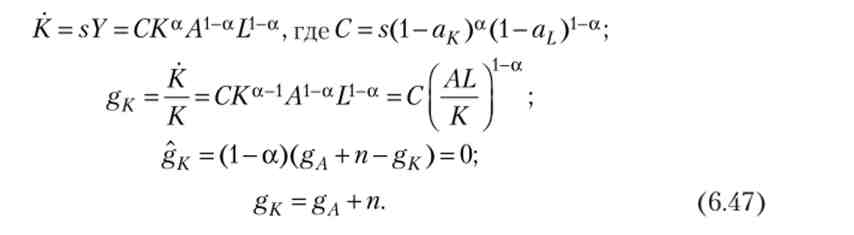
Крива незмінного темпу зростання капіталу описується рівністю (6.47): вище цієї прямої темп приросту капіталу падає, а нижче її - зростає. Крива незмінного темпу зростання знань - безліч точок в площині (g_A, g_K), для яких геми зростання знань незмінний.

З (6.45) отримаємо формулу темпу приросту капіталу. Розділимо її на Л, прологарифмируем і продифференцируем її, отримаємо формулу темпу приросту показника g_A. Прирівняємо нулю її праву частину, отримаємо формулу кривої незмінного темпу зростання знань:

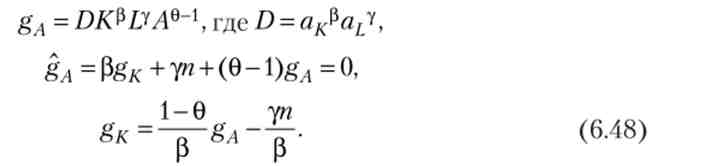
Крива незмінного темпу зростання знань описується рівністю (6.48): вище цієї прямої тими приросту капіталу зростає, а нижче її - падає.

Стаціонарна точка - точка перетину кривих незмінного темпу зростання знань і постійного збільшення капіталу.

Визначимо параметри стаціонарного зростання. Нехай населення зростає (П> 0), тоді (6.47) перетинає вісь ординат в позитивній точці, а (6.48) - в негативній. Прямі лінії перетинаються, якщо нахил прямої (6.48) більше, ніж нахил прямої (6.47). Звідси умова стаціонарного зростання:

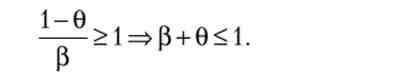
З (6.45) випливає, що ця умова виконана, так як р + у + 0 = 1. Таким чином, при зроблених припущеннях завжди існує єдине стаціонарне стан.

Вирішимо систему рівнянь (6.47) і (6.48), отримаємо стаціонарні значення темпів приросту капіталу і знань:

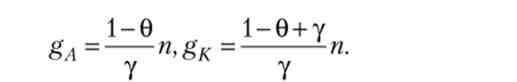
Стаціонарний темп зростання отримаємо логарифмування і диференціюванням формули (6.44) з урахуванням (6.47):

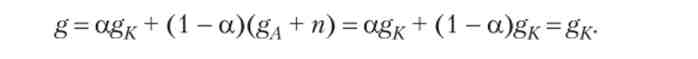
Отже, стаціонарний темп економічного зростання дорівнює стаціонарного темпу приросту капіталу, він не залежить від параметра виробничої функції доходу, а також від пропорцій, у яких розподілені працю і капітал між секторами економіки. Він перевищує темп приросту населення на величину темпу приросту обсягу накопичених знань. Рівність (6.47) трактують як розкладання темпу економічного зростання на інтенсивну складову (темп приросту знань) і екстенсивну (тими приросту населення).

1. Динаміка руху цін ф'ючерсів, акцій і валют
   Фінансовий ринок складний і неоднорідний: він складається з різних субринков. Коливання цін на них корелюють один з одним. В одних випадках коливання синхронізуються, в інших між коливаннями на різних ринках існує певний лаг часу. Існують також відмінності в рівнях коливальних рухів. Найчастіше
2. Динаміка поблизу стаціонарної точки
   У моделі Рамсея - Каса - Куіманаса функція дорівнює нулю в стаціонарній точці (k *, с *), тому її диференціал дорівнює З (2.31) помічаємо, що темпи зростання відхилень споживання і фондоозброєності залежать лише від ставлення цих відхилень. Розглянемо випадок, коли цей показник незмінно одно
3. Динамічний процес руху до рівноваги але Неша
   Відзначимо, що точка Л3 може бути отримана як межа наступного динамічного процесу, в якому очікування формуються адаптивно: Співвідношення (13.3) означає, що комбінація (n t ,y t ) є при y t = Р (я, -rcf) рішенням завдання Іншими словами, на кожному кроці t держава мінімізує свою функцію втрат
4. Динамічна функція сукупного попиту
   Побудована в параграфі 6.3 функція сукупного попиту показує, яким буде обсяг дійсного попиту при різних значеннях рівня цін. В умовах довготривалого зростання рівня цін при визначенні величини сукупного попиту потрібно враховувати два додаткових обставини, пов'язаних з тим, що величина сукупного
5. Держава, поняття і цілі грошово-кредитної політики держави
   Третій важливий агент, зазвичай присутній в макроекономічних моделях, - держава. Воно розглядається в макроекономіці зазвичай як єдине ціле, без поділу на уряд і ЦБ. Передбачається, що держава діє в цілях збільшення суспільного добробуту, використовуючи інструменти фіскальної та грошово-кредитної
6. Частково мобільний капітал
   Звернемося тепер до більш реалістичного нагоди, коли капітал може перетинати кордони, однак не є повністю мобільним. Це відповідає реальному стану справ, так як інвесторам часто простіше вкладати кошти у власній країні, де відомі норми (як формальні, так і неформальні) ведення бізнесу, ніж
7. Базові гіпотези: Монте-Карло, Фріша - Слуцького
   Торгівля нафтою, як і багатьма іншими масовими біржовими товарами, є досить дивною, тому що інвестори насправді не купують і не продають нафту, вони купують і продають право на нафту в якийсь віддалений день у майбутньому (що прийнято називати торгівлею ф'ючерсами) . Основна ознака такої угоди
8. Австрійська економічна школа
   Людвіг фон Мізес вирішив, що кількісна теорія грошей в своїй основі правильна, але критично ставився до положення про пропозицію грошей без відповідного попиту на них і поясненню причин, які змінюють попит на гроші. Тому Мізес вважав, що класична кількісна теорія не в змозі пояснити механізм