
| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Спеціальний людський капітал - якості людини, придбані в процес трудової діяльності і служать джерелом доходу. У параграфі 6.2 розглядався загальний людський капітал, який формується в процесі навчання в навчальному закладі.
Передбачається, що темп зростання ВВП (1 + g) залежить лише від накопиченого досвіду, або професійного стажу (z):

де а > 0.
Досвід збільшується з часом, в початковий момент він мінімальний і дорівнює одиниці, а темп економічного зростання (g) дорівнює нулю. Передбачається, що приріст накопиченого досвіду є статечна функція його обсягу: чим більше досвід, темп швидше він зростає:
де b > 0; 0 < р < 1.

Рішення диференціального рівняння (6.50) з урахуванням 2 (0) = 1 має вигляд
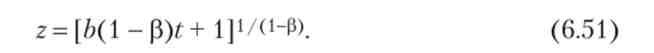
Підставами (6.51) в (6.49), отримаємо формулу темпу зростання:
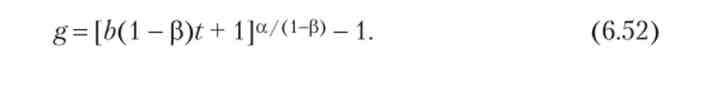
Висновки з рівності (6.52):
1) якщо а + р > 1, то темп зростання збільшується лавиноподібно, якщо а + + р < 1 - темп уповільнений, якщо а + р = 1 - темп зростання прямо пропорційний довжині проміжку часу:
 )
)
приклад
а = р = 0,5; b = 0,06. Тоді а + р = 1, і відповідно до (6.53) через рік тими економічного зростання складе 0,06? 0,5 - 1 = 0,03 (3%), через два роки - 6%, через три роки - 9%.
6.4.2. Модель з навчанням на робочому місці (Лукас)
Дві галузі виробляють близькі замінники, випуск кожної галузі дорівнює добутку обсягу простого праці і обсягу спеціального людського капіталу одного працівника (ефективності праці), т. Е. Випуск пропорційний витратам ефективного (корисного) праці. Незмінний обсяг простого праці (L) Розподілений між галузями: ах і а2 - частки витрат праці по галузях:

де Qj, Q2 - випуски; h{, h2 - обсяги спеціального людського капіталу на одного працівника (ефективність праці).
Приріст ефективності праці в галузі пропорційний поточному значенню ефективності, рівнем технічного розвитку галузі (5), а також частці витрат праці в галузі:
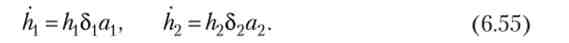
Нехай рівень технічного розвитку першої галузі більше: 8Х > 62. Наприклад, в ній огірки вирощують в теплиці, а в другій - на відкритому грунті.
Ціна першого товару дорівнює 1, другого - с /. Якби корисність продуктів була рівною, то з часом розорилася б галузь з більшою ціною, тому при довготривалій конкуренції галузей продукт з більшою ціною має також велику корисність.
Стаціонарний зростання - ціни продуктів незмінні в часі і такі, що рух робітників між галузями не змінює доход.
Дохід дорівнює сумарної вартості продукції обох галузей (У), з урахуванням рівності а2 = - ал маємо:
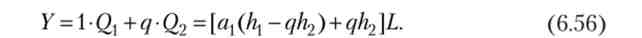
З (6.56) випливає, що умова стаціонарного зростання виконується, т. Е. Дохід не залежить від а1У якщо ціна в другій галузі дорівнює відношенню показників ефективності праці:

З (6.57) випливає, що оскільки ціна q постійна, то при стаціонарному зростанні ефективність праці в обох галузях росте рівним темпом:

Тоді темп економічного зростання дорівнює темпу приросту ефективності праці, що випливає з формули стаціонарного доходу:
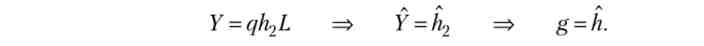
З огляду на рівності (6.55), ми приходимо до висновку, що розподіл праці між галузями визначається показниками рівня розвитку галузей, причому більш розвинена галузь використовує менший обсяг праці:
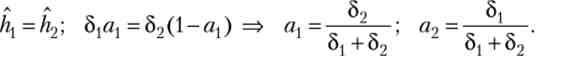
Отже, темп економічного зростання дорівнює середньої геометричної величиною показників рівня розвитку галузей:
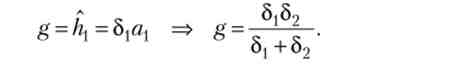
Таким чином, навчання працівників на робочому місці викликає гарантоване зростання доходу при постійній чисельності населення.
Рівновага домогосподарства - домогосподарство досягає максимальної корисності при заданій величині реального ВВП (доходу).
Окремий випадок 1. Корисність домогосподарства виражається функцією з постійною еластичністю заміщення:
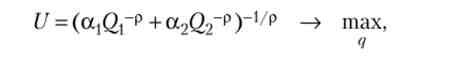
де еластичність заміщення:
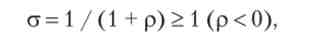
де (Х | і а2 - відносні корисності продуктів + а2 = 1). Обмеження завдання - ВВП дорівнює сумарній виручці галузей:
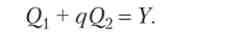
Вирішимо задачу на умовний екстремум:
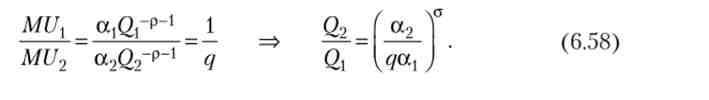
Звідси чим вище корисність продукту і чим нижче його ціна, тим більше його проходження митного кордону при рівновазі домогосподарства.
Загальна рівновага - домогосподарство максимізує корисність при стаціонарному зростанні. Умова загальної рівноваги отримаємо, розділивши два рівності (6.54) одне на інше і перетворивши це відношення з урахуванням (6.57). Прирівняємо отримане вираз для відношення випусків і праву частину (6.58):
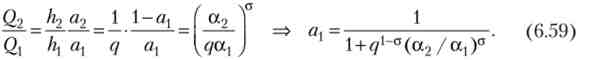
Отже, частка працівників більш розвиненою галузі зростає при скороченні корисності і зростанні ціни продукції іншої галузі.
Стаціонарну ціну визначимо, прирівнюючи два вираз для стаціонарної частки працівників першої галузі:
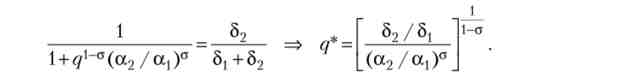
Якщо ціна другого продукту більше <?*, То галузь розориться, і буде проводитися тільки перший продукт. Якщо вона менше q *, то буде проводитися тільки другий продукт.
Окремий випадок 2. Корисність домогосподарства виражається функцією Кобба - Дугласа:
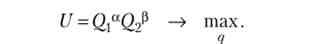
Тоді умова рівноваги домогосподарства:
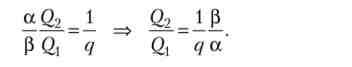
Умова загальної рівноваги:
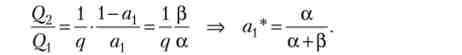
Отже, в разі загальної рівноваги:
Якщо частка працівників першої галузі не дорівнює а *, то стан не рівноважний. Якщо частка більше а *, то ціна другого товару зростає, і з часом буде проводитися тільки перший продукт. Якщо вона менше а *, то ця ціна падає, і з часом буде проводитися тільки цей продукт.