Страхування

корисність споживача (І) залежить від його багатства. Він може знаходитися в двох станах: у першому стані (при хорошому результаті) його початкове багатство (А) повністю зберігається, а в другому стані (при поганому результаті) воно скорочується на величину збитку b внаслідок непередбаченого випадку, наприклад пожежі. Нехай ймовірність гарного результату - рр поганого - р₂, тоді середня величина багатства дорівнює

Страховик - це фірма, яка в обмін на страховий платіж (вартість страхового поліса) гарантує виплату страхового відшкодування (d) власнику багатства (страхувальникові) в разі настання поганого результату.

Розглянемо найпростіший випадок, коли страхувальник бажає повністю застрахуватися від нещасного випадку, т. Е. Зберегти величину свого багатства при будь-якому результаті на початковому рівні. Позначимо шукану величину страхового платежу через R, тоді багатство при хорошому і поганому результаті, а також його середнє значення дорівнює a- R. Оскільки воно повинно дорівнювати початкового значення (3.51), отримуємо рівняння щодо R. Вирішимо його:

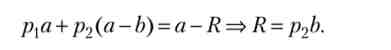
Отже, для забезпечення повного страхування ризику величина страхового платежу (ціна поліса) повинна становити частку втраченого багатства (збитку), що дорівнює ймовірності настання поганого результату.

приклад

Багатство - 100, збиток - 30, ймовірність пожежі - 10%, тоді при повному страхуванні вартість страхового поліса дорівнює 0,1 - 30 = 3, а страхове відшкодування дорівнює 30. Середня величина багатства до страхування дорівнює 0,9 - 100 + 0, 1 - 70 = 97, після страхування вона не зміниться і складе 0,9 - 97 + 0,1 - 97 = 97.

Частка страхової премії - це відношення страхового платежу до величини страхового відшкодування: у = R / d. У разі повного страхування виконується рівність b = d, а частка страхової премії дорівнює ймовірності поганого результату:

Показник 1 / у дорівнює страховому відшкодуванню, яке отримає страхувальник на один рубль вартості страхового поліса при настанні поганого результату. Тому страхувальник зацікавлений в збільшенні цього показника, а страховик - в його зменшенні. Якщо фактичне значення показника перевищує теоретичний рівень 1 / р₂, то страховик несе збитки, в іншому випадку він отримує прибуток.

У ряді випадків умова повного відшкодування (3.52) може не виконуватися.

Функція очікуваної корисності страхувальника дорівнює середньому зваженому значенням корисності для двох можливих результатів:

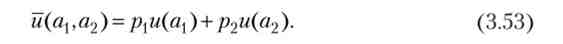
При хорошому результаті багатство дорівнює різниці початкового багатства і страхового платежу (а, = а - yd), а при поганому результаті воно дорівнює сгоімості врятованого багатства (А - b) Плюс страхове відшкодування мінус страховий платіж: а₂ = А - b + d - yd. Середня величина багатства дорівнює

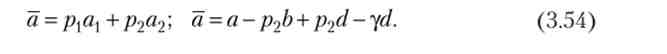
Розглянемо дві моделі страхового поведінки.

1. Страхувальник максимізує корисність очікуваного доходу і (а).

Для визначення умови рівноваги прирівняємо нулю похідну функції корисності за величиною страхового відшкодування:

У рівновазі частка страхового відшкодування дорівнює ймовірності поганого результату, т. Е. Виконано умову повного відшкодування (3.52), при цьому рівноважний стан єдино. Даний тип поведінки характерний для споживача, не схильну до ризику, оскільки для нього виконується й < і (з), І тому він орієнтується на праву частину даного нерівності, м. Тобто на корисність відомої величини багатства.

2. Страхувальник максимізує функцію очікуваної корисності w, варіюючи вартість страхового відшкодування.

Даний тип поведінки характерний для споживача, схильного до ризику, оскільки для нього виконується й і (с)_у і тому він орієнтується на ліву частину даного нерівності, т. е. на очікувану (випадкову) величину корисності.

підставами вираження а_Л і а₂ в цільову функцію (3.53), потім прирівняємо нулю похідну по d:

З (3.55) випливає, що при виконанні умови повного страхування у= р₂ граничні корисності і обсяги багатства в обох станах рівні:

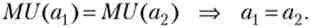
Стан рівноваги споживача не єдино, оскільки для кожної частки страхового відшкодування є свої параметри рівноваги. Нехай страховик встановлює знижений значення цієї частки: у < р₂. Тоді права частина рівності (3.55) більше одиниці, і гранична корисність при хорошому результаті більше граничної корисності при поганому результаті. Оскільки страхувальник схильний до ризику, гранична корисність зростає, і рівноважна величина багатства при хорошому результаті більше, ніж при поганому результаті:

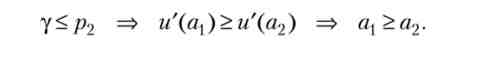
Окремий випадок. Споживач схильний до ризику, його функція корисності: і = а², при цьому у < р₂. З (3.55) випливає умова рівноваги:

де 0 > 1.

Вирішивши отримане рівняння, визначимо рівноважну величину страхового покриття:

З (3.56) випливає, що при виконанні умови повного страхування (3.52) страхове покриття одно збитку, оскільки величина 0 дорівнює одиниці.

приклад

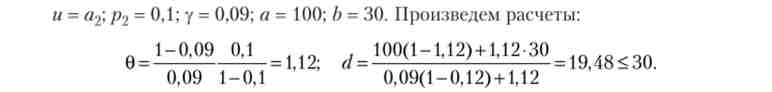
Отже, на знижену частку страхового покриття (вигідний для нього підвищений коефіцієнт 1 / у) схильний до ризику страхувальник реагує зниженою величиною страхового відшкодування. У рівновазі його багатство при хорошому результаті одно 98,25, при поганому результаті - 87,73. Ставлення цих величин дорівнює 0 = 1,12.

1. Ціноутворення за недосконалої конкуренції, рівновага при досконалої інформації (Лукас - Фелпс)
   Нехай на ринку є п однотипних товарів. Ціна г-го товару дорівнює Р " його відносна ціна близька до одиниці і дорівнює Р, / Р, де Р - рівень цін. Зміна переваг споживачів - відхилення обсягу попиту на товар від статичного обсягу попиту. Змінений обсяг попиту дорівнює ZjQj, де Q, - статичний
2. Ціни і їх роль в національному рахівництва, види цін в національному рахівництва
   В результаті вивчення даного розділу студент повинен: знати види і роль цін, що застосовуються в макроекономічному аналізі; основні індекси цін; відмінності номінальних і реальних показників; причини відмінностей в цінах; вміти розраховувати основні види цін і основні індекси; використовувати
3. Цикли та інфляційні очікування (Лайдлер)
   Ступінь завантаження виробничих потужностей (х () - відношення фактичного (y t ) і потенційного ВВП (Y t ) x t = y t / Y t . Досліджуємо темпи зростання потенційного ВВП (k t = Y t / Y t _ {), рівня цін (g t = p t / p t _ x ) і грошової маси (m t = M t / M t _ x ). Попит на гроші отримаємо
4. Тривалість руху до динамічної рівноваги
   Відповідно до моделі Солоу - Свана при відсутності технічного прогресу або екзогенному трудосберегающих технічному прогресі економіка, яка не перебуває в стані динамічної рівноваги, обов'язково прийде до нього через певний час. В якому стані частіше знаходиться економіка, залежить від тривалості
5. Теорії людського капіталу, людський капітал: загальний і спеціальний
   У сучасній економіці продуктивність працівника залежить в першу чергу від інвестицій в освіту. Ця теза лежить в основі теорії людського капіталу Г. Беккера. Людський капітал - це придбані якості людини (знання, вміння, досвід), які впливають на його продуктивність і служать джерелом його доходу.
6. Теорія питання
   Приватизація і дерегулювання - одне чи це й те саме? приватизація означає особливий спосіб переведення активів і управлінських функцій з державного в приватний сектор. Мета приватизації - створення інституту приватних власників, широкого кола невеликих акціонерів, розвиток фондового ринку
7. Теорія економічних циклів, поняття економічного циклу
   Теорія економічних циклів поряд з теорією економічного зростання пояснює характер розвитку економіки в часі. Статистичні дані свідчать, що зміна показників, що характеризують результати національних господарств, змінюються не монотонно, а колебательно. На рис. 9.1 показані темпи приросту реального
8. Технології і структура ринку
   Продукт виробляється декількома фірмами, причому фірма застосовує або стару технологію А, або нову технологію В. Зарплата працівника дорівнює одиниці. Власники фірми є також її працівниками, їх чисельність (L) незмінна, їх дохід (У) дорівнює сумі зарплати (I) і прибутку (л): технологія А.