| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Фінансова бульбашка - необмежене зростання ціни фінансового активу. Нехай в поточний момент часу t ціна акції дорівнює pt, а дивіденд в кінці року гарантовано рівний dt. У наступні періоди ціна і дивіденди характеризуються своїми очікуваними значеннями E [pt + i] і E [dt + i, де i - номер року; Е - оператор математичного очікування, його властивості:
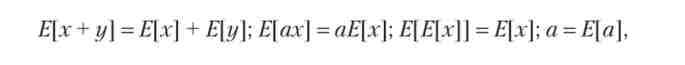
де х, у - випадкові змінні; а - відома константа.
Очікуваний дохід з акції - сума очікуваного приросту її поточної ціни і відомої величини дивіденду, він дорівнює
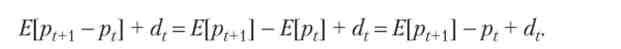
Прибутковість акції (г) - відношення очікуваного доходу з акції до її поточною ціною:
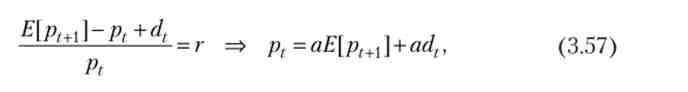
де а = 1 / (1 + г) 1.
Ми отримали рекурентне співвідношення щодо поточної ціни акцій, в якому вона виражена через очікувану ціну в наступному періоді, будь-яке його рішення pt задовольняє умові

Фундаментальне рішення рекурентного рівняння ціни акції - сума нескінченного дисконтированного потоку очікуваних дивідендів:

Отримаємо формулу для ціни в наступному періоді, замінивши в рівність (3.59) індекс t на індекс t + 1:

Доведемо, що фундаментальне рішення (3.59) дійсно є рішенням рекуррентного рівняння (3.57), для цього підставимо pf + 1* З рівності (3.60) в праву частину (3.57), з огляду на dt = E [dt:
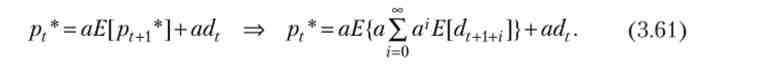
Перетворимо (3.61), використовуючи властивості математичного очікування і враховуючи, що поточний дивіденд є відомою константою:
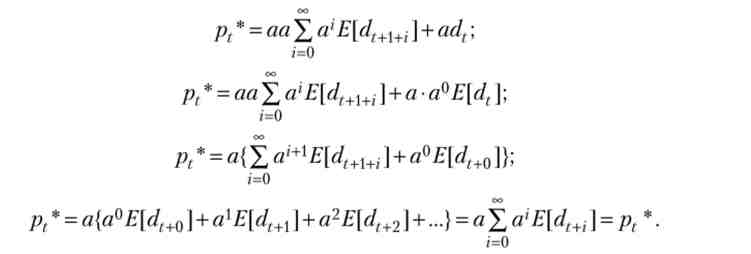
Ми отримали тотожність, а значить, вираз (3.59) дійсно задає рішення рівняння (3.57). Однак це рішення може бути не єдиним. Визначимо умови, при яких рішенням служить також сума фундаментального рішення і деякої необмеженої нескінченної послідовності bt

Спекулятивна складова ціни (bt) - різницю поточної ціни (pt) і її фундаментального значення (Р *).
Підставами (3.62) у вихідне рівняння динаміки (3.57), використовуємо властивості математичного очікування і той факт, що р * є рішенням, т. е. виконується рівність (3.58):
Отже, сума фундаментального рішення і послідовності bt є рішенням рівняння (3.57) за умови, що виконується оптимістичне умова (3.63), т. е. очікувана в наступному періоді ціна незмінно перевищує поточну ціну. оскільки а 1, то спекулятивна складова bt зростає в геометричній прогресії, і тому рішення (3.62) є фінансовим міхуром. Зауважимо, що міхур може існувати при постійному рівні дивідендів за рахунок очікування прискореного зростання ціпи акції. При нульовій ставці відсотка міхур виникнути не може.
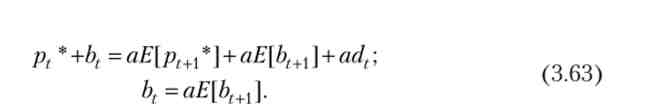
приклад
Прибутковість акцій дорівнює 10%, дивіденд незмінно дорівнює 3 од. У поточному році якісь позитивні очікування збільшують поточну ціну акції на 2 од. щодо фундаментального рішення, а в подальшому ці очікування збільшують спекулятивну складову ціни на 10% на рік. тоді а = 1 / 1,1 = 0,91, і фундаментальна складова ціни акції дорівнює
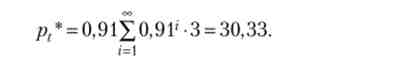
Спекулятивна складова ціни задається співвідношенням:
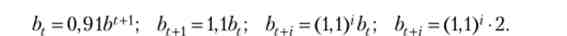
Ціна акції в вихідному році дорівнює 32,33 од., Через рік - 32,53 од., Через 20 років - 43,78.
Вибухаючий міхур - спекулятивна складова ціни акції необмежено зростає, але при цьому може приймати нульові значення.
нехай послідовність bt задовольняє умові міхура (3.63). Візьмемо деяке позитивне число q 1 і складемо іншу послідовність b 't, значення якої в наступний момент приймають значення bt / а з ймовірністю q і значення 0 з ймовірністю (1 - q)

Доведемо, що дана послідовність задовольняє умові міхура (3.63). З (3.65) випливає:
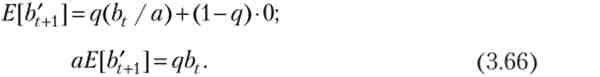
Праві частини рівності (3.64) і (3.66) рівні, прирівняємо їх ліві частини і отримаємо умову міхура (3.63):
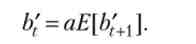
Отже, послідовність 6 / описує вибухає міхур.