
| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Уряд продає бескуіоннис облігації на суму В при ставці прибутковості г, безризикова прибутковість (ставка відсотка) дорівнює i. До моменту погашення облігацій уряд збирає податки в сумі Т.
Дефолт - сума зібраних урядом податків менше суми, необхідної для погашення облігацій. Умова дефолту:

Якщо виконана умова (3.67), то інвестори втратять всі вкладені кошти, в іншому випадку вони отримають суму боргу з відсотками. Передбачається, що прибутковість облігацій більше ставки відсотка (R> i).
Рівновага - очікувана прибутковість облігацій (її математичне очікування) дорівнює ставці відсотка: E [r] = i. В цьому випадку інвесторам байдуже, в якій актив вкладати кошти. При ймовірності дефолту, рівній р, виконується рівність
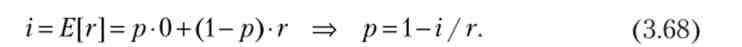
З (3.68) випливає, що чим вища доходність облігацій і чим нижче ставка відсотка, тим вище ймовірність дефолту. Імовірність дефолту дорівнює нулю, якщо обидві прибутковості однакові. Ми вважаємо податкові надходження Т випадковою величиною з функцією розподілу Е, тоді ймовірність дефолту може бути записана так:
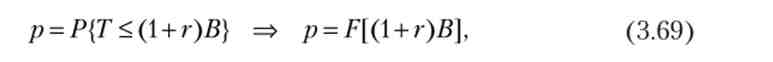
де Р позначає ймовірність події.
нехай Т{ - мінімальна (песимістична) сума податкових надходжень. Імовірність дефолту дорівнює нулю, в разі коли сума погашення менше цього значення:

З (3.70) випливає, що дефолту можна не побоюватися, якщо прибутковість облігацій менше, ніж ставлення мінімально можливої суми податкових зборів і суми боргу за вирахуванням одиниці. Якщо мінімальні податкові збори настільки малі, що не перевищують суми боргу, то «безпечних» ставок прибутковості не існує.
Нехай 7 * 2 - максимальна (оптимістична) сума податкових надходжень. Тоді ймовірність дефолту дорівнює одиниці, в разі коли сума погашення більше цього значення:
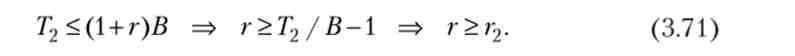
З (3.71) випливає, що дефолту неможливо уникнути, якщо прибутковість облігацій більше, ніж ставлення максимально можливої суми податкових зборів і суми боргу за вирахуванням одиниці. Якщо максимальні податкові збори настільки малі, що не перевищують суми боргу, то будь-яка прибутковість облігацій є «небезпечною», т. Е. Загрожує дефолтом.

Оскільки обидві функції (3.68) і (3.69) зростають зі зростанням прибутковості г, то можуть існувати кілька точок рівноваги. Крива (3.68) - гіпербола, що проходить через точку (г, 0). Крива (3.69) визначається характером розподілу змінної випадкової Т і проходить через точки (гх, 0) і (г2, 1).
нехай змінна Т розподілена рівномірно, тоді функція розподілу (3.69) - трехзвенная ламана з похилим відрізком, що з'єднує точки (г ,, 0) і (г2, 1). Розглянемо стану з єдиною рівноважною ставкою прибутковості для двох крайніх випадків.
Окремий випадок 1. Ситуація зі збором податків несприятлива і мінімальна сума податкових надходжень дорівнює розміру боргу, т. е. гх - 0. Тоді умова рівноваги (3.72) зводиться до квадратного рівняння щодо м
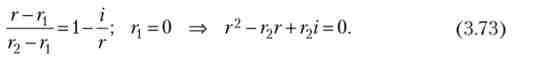
Дискримінант рівняння (3.73) D = г2(г2 - 4г) дорівнює нулю, якщо г2 = 47, тоді рівновагу єдино. В цьому випадку г * = 2г, а ймовірність дефолту дорівнює р = 1 - г / 2г = 0,5 (50%). Таким чином, рівноважна прибутковість в два рази більше ставки відсотка. При високій ставці відсотка г2 < 4г дискриминант негативний і рівновагу неможливо. При низькій ставці г2 > 4г є два рівноважних значення прибутковості, і різниця між ними скорочується зі зростанням ставки відсотка. Реалізація на практиці того чи іншого стану рівноваги залежить від очікувань інвесторів.
Окремий випадок 2. Ситуація зі збором податків сприятлива, і мінімальна сума податкових надходжень дорівнює розміру боргу з відсотками, т. е. r = i. Тоді умова рівноваги (3.72) зводиться до квадратного рівняння щодо г:
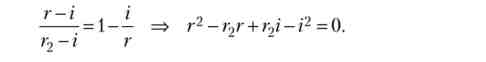
Дискримінант даного рівняння дорівнює нулю, якщо г2 = 27, тоді рівновагу єдино. В цьому випадку г * = i, а ймовірність дефолту дорівнює нулю: р = - 7/7 = 0.