| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
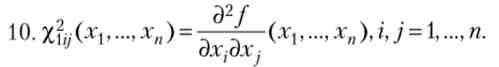
значення функції Xuj характеризує динаміку зміни граничної продуктивності j-го ресурсу при зміні кількості / -го ресурсу на одиницю (початкової вважається точка хх,..., хп).
Перераховані характеристики не є незалежними. Вимоги, що накладаються на одні характеристики, обмежують можливості зміни інших.
Поняття еластичності заміни факторів є одним з основних понять теорії виробничих функцій. Еластичність заміни факторів є характеристикою «самостійності» впливу окремих аргументів виробничої функції на її значення.
Діаметрально протилежними при заданих початкових обсягах ресурсів (факторів) є такі ситуації:
У ситуації а) зменшення «впливового» фактора неможливо компенсувати за рахунок збільшення інших факторів, в той час як в ситуації б) така компенсація в принципі можлива (хоча, можливо, зажадає залучення значних обсягів компенсуючих ресурсів). У першому випадку говорять про відсутність заменяемости факторів, у другому - про її наявність. І та і інша ситуація зустрічається в економічній практиці. Серед безлічі виробничих функцій є функції, що відображають ці ситуації. Розглянемо функцію
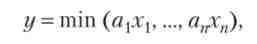
де у - обсяг випуску продукції; хі ..., хп - показники факторів виробництва; alf ..., ап - параметри виробничої функції (ця функція називається функцією Леонтьєва). Тут в кожній точці х = (xv ..., хп) величина у визначається тим з показників xif для якого величина apCj мінімальна. Збільшення випуску можливо тільки при збільшенні цього показника xit інші показники (в межах малих змін) на у не впливають. Протилежну ситуацію описує лінійна функція у = а{хj + ... + а} Тхп. Тут пі один з факторів ні в одній точці не володіє «винятковими повноваженнями» на збільшення обсягу випуску. Останній реагує на зміну рівня кожної з вхідних в модель змінних хі ..., хп. Природно вважати, що заменяемость факторів у функції Леонтьєва дорівнює нулю, а в лінійної функції - нескінченності.
Питання про можливість заміни факторів у виробничій функції завжди вирішується по відношенню до того набору ресурсів, який фігурує в якості аргументів виробничої функції. Якщо факторами служать укрупнені показники розмірів виробничих фондів і чисельності персоналу, а результат виробництва вимірюється вартісними обсягом товарної продукції (оборотом), то питання про еластичність заміни зводиться до аналізу можливості взаємного заміщення праці.
При аналізі можливостей заміни ресурсів в різних моделях виробничого процесу слід чітко фіксувати рівень моделювання. Якщо вихідними показниками моделі є кількості виробів кожного з видів, то заменяемость має місце, коли випуск продукції даної кількості і номенклатури можливий за допомогою різної кількості ресурсів. Тут ненульова еластичність заміни факторів є результатом наявності різних технологій виробництва однієї і тієї ж продукції (технологічна заменяемость).
На рівні ж агрегированной економічної технології заменяемость одного фактора іншими виникає, якщо за допомогою різних наборів ресурсів хь ..., хп і ху ..., х 'п можна виробити продукцію одного і того ж обсягу (за умови, що ця продукція призначена для задоволення аналогічних функціональних потреб). Таким чином, на рівні виробничих функцій оцінюється не стільки технологічна, скільки економічна заменяемость факторів.