| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
У більшості моделей макроекономіки мети економічного суб'єкта, в тому числі суспільства в цілому, формалізуються у вигляді завдання максимізації деякої функції, яка називається цільовою. Основні види цільової функції - виробнича функція і функція корисності.
Виробнича функція - залежність реального ВВП (доходу) від витрат ресурсів. Граничний продукт ресурсу дорівнює приросту доходу при збільшенні витрат ресурсу на одиницю - в разі дифференцируемой виробничої функції це її приватна похідна. Граничний продукт падає з ростом витрат ресурсу. Ізокванта - крива, що зображує безліч наборів ресурсів, що забезпечують однаковий дохід.
Однорідна виробнича функція - функція, що володіє властивістю: зростання витрат всіх ресурсів в t раз призводить до зростання доходу в ft раз:
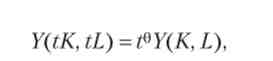
де L, К - витрати праці і капіталу.
Зростаючий ефект від масштабу виробництва має місце в однорідної виробничої функції, коли 0 > 1, регресний ефект від масштабу - коли 0 < 1, постійний ефект від масштабу - коли 0 = = 1. В останньому випадку збільшення витрат кожного ресурсу на а% викликає зростання доходу на а%.
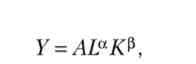
Виробнича функція Кобба - Дугласа має вигляд статечної функції двох змінних:
де а, (3 - коефіцієнти еластичності доходу за витратами праці і капіталу, рівні відносного зміни доходу при збільшенні аргументу на 1%; А - продуктивність економіки, рівна доходу при одиничних витратах ресурсів.
Зростаючий ефект від масштабу має місце при а + р > 1: збільшення витрат ресурсів в деяке число раз викличе зростання випуску в більше число разів. Зростаючий ефект має місце при а + р < 1, постійний ефект - при а + р = 1.
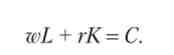
Знайдемо умову максимуму функції доходу при заданій ціні праці (Ге), ціною капіталу (г) і сумарної вартості ресурсів (С). Маємо лінійне обмеження:
Складемо функцію Лагранжа (? А), для цього з цільової функції віднімемо обмеження (попередньо всі його члени запишемо в ліву частину рівності), помножене на невідомий параметр Лагранжа (А.). Потім прирівняємо нулю її похідні і розділимо отримані рівняння один на одного. Ми приходимо до висновку, що в стані рівноваги відношення граничних продуктів праці (MPL) І капітана (МРК) дорівнює відношенню їх цін:
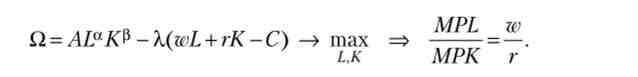
приклад
Задані параметри функції доходу, ціни ресурсів і загальні витрати. Визначимо рівноважні (оптимальні) витрати ресурсів, при яких дохід максимальний. дано: А = 1; а = 0,4; р = 0,6; w = 4; г = 5; С = 200. Дорівняємо відношення приватних похідних цінами ресурсів, висловимо витрати капіталу через витрати праці і підставимо цю формулу в обмеження. Отримаємо оптимальні витрати ресурсів:
Виробнича функція Леонтьєва має вигляд
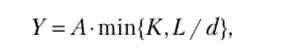
де d - заданий число працівників на один верстат (одиницю капіталу), т. е. чисельність «бригади»; L / d - кількість бригад; А - продуктивність економіки, рівна доходу при використанні одного верстата і однієї бригади. Є постійний ефект від масштабу.
На відміну від функції Кобба - Дугласа, збільшення витрат одного ресурсу може не викликати зростання доходу. Ізокванта - прямий кут зі сторонами, паралельними осям, причому координата «праця» вершини кута в d раз більше координати «капітал».
Максимізували функцію Леонтьєва при заданих цінах і вартості ресурсів. Обмеження збігається з випадком функції Кобба - Дугласа. При максимальному випуску немає невикористовуваних ресурсів, т. Е. Число верстатів дорівнює числу бригад. Підставами ця умова в обмеження, отримаємо оптимальні витрати ресурсів:
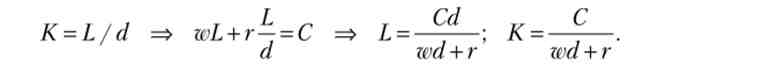
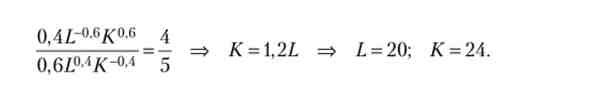
приклад
Максимізували функцію Леонтьєва. дано: d = 4; w = 4; г = 5; З = 200. Тоді з формул слід: оптимальні витрати праці - 38,1, капіталу - 9,5.
Лінійна виробнича функція має вигляд
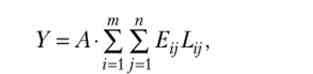
де Ljj - чисельність працівників / -го соціального типу, зайнятих на робочому місці j-го типу; еу - ефективність праці працівників / -го типу, зайнятих на робочому місці j-го типу (Еу > 1); т - число типів працівників; п - число типів робочих місць; А - продуктивність економіки, рівна доходу при використанні одного працівника з нижчої (одиничної) ефективністю.
В даному випадку є постійний ефект від масштабу, а граничний продукт праці працівника дорівнює ефективності його праці.
Максимізували лінійну функцію при заданій чисельності соціальних груп і робочих місць кожного типу, а також значних ефективності. Це завдання лінійного програмування, її рішенням служить план призначень працівників на робочі місця. Він має форму матриці {Lyj, у якій сума елементів рядка дорівнює чисельності працівників даного типу (я,), а сума елементів стовпця - числу робочих місць даного типу (By):
Це аналог транспортної задачі про мінімізації витрат при доставці продукції із заводів з випусками ах по магазинам з обсягами продажів Ьу Вона вирішується методом потенціалів: 1) підбирається базовий план призначень, в якому є рівно (Т + п - 1) ненульових клітин; 2) підбираються допоміжні змінні (потенціали) а ,, р7, такі, що їх сума дорівнює ефективності праці для ненульових клітин. Якщо їх сума не менше ефективності праці для ненульових клітин, то план оптимальний, а випуск максимальний, в іншому випадку план вимагає поліпшень.
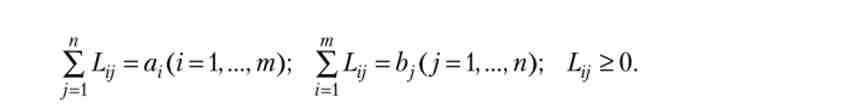
приклад
дано: Л = 1, чисельність соціальних груп - 40 і 60, число робочих місць кожного типу - 20, 10 і 70, значення ефективності праці наведені в табл. 1.3 в чисельнику дробу, в знаменнику - елементи оптимального плану призначень. Потрібно оптимально розподілити 100 працівників по робочих місцях.
Визначення максимуму лінійної виробничої функції методом потенціалів
Таблиця 13
|
Чисельність робочих місць, потенціали |
|||||
|
20 |
10 |
70 |
|||
|
Чисельність працівників, по- циал |
40 |
2/0 |
1/0 |
5/40 |
0 |
|
60 |
4/20 |
2/10 |
3/30 |
-2 |
|
|
р, |
6 |
4 |
5 |
||
Сума потенціалів для нульового призначення в клітці (1,1) більше ефективності праці: 0 + 6 > 2, а для нульового призначення в клітці (1,2) виконується аналогічне рівність: 0 + 4 > 1. Тому план призначень оптимальний, а максимальний дохід дорівнює Y = 5 - 40 + 4 - 20 + 2 - 10 + 3 - 30 = 390.
Функція корисності - залежність корисності від обсягів споживаних благ, до яких можуть відноситися споживана частина доходу, грошові накопичення, величина багатства і ін. На відміну від виробничої функції, функція корисності залежить від суб'єктивних переваг людей і може приймати негативні значення, однак завдання її максимізації вирішується аналогічно нагоди виробничої функції.
приклад
Суспільство прагне найкращим чином розділити заданий обсяг благ (С) на дві частини: споживання в молодості (Cj) і в старості (С2). Функція корисності відноситься до класу Кобба - Дугласа:
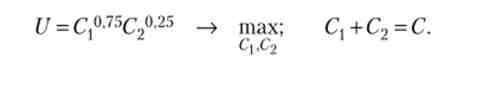
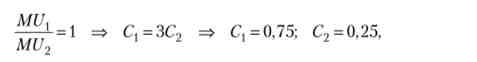
де MU, MU2 - граничні корисності (приватні похідні) функції корисності.
З вигляду функції випливає, що значимість (еластичність) споживання в молодості в три рази більше, ніж старості. Не дивно, що оптимальний обсяг споживання в молодості виявився також в три рази більше.