Критерій Парето і домінуючі стратегії

Ефективність - співвідношення корисного результату і витрат. Якщо виробляють один продукт з одного ресурсу, то ефективність дорівнює відношенню випуску продукту до витрат ресурсу. Але для всієї економіки ефективність виміряти складно через різноманітність товарів, і крім того, суспільні блага не володіють ринковою ціною, а деякі товари породжують значні зовнішні ефекти. Наприклад, книга і пляшка горілки дорівнює вартості мають різну суспільну корисність.

Критерій ефективності Парето стверджує, що один з варіантів виробництва ефективніше іншого, якщо він краще за всіх розглянутих аспектів. Даний критерій не передбачає будь-якого способу розрахунку ефективності, зате він дозволяє порівнювати ефективність деяких (не всіх) варіантів виробництва, т. Е. Наборів випусків продуктів і витрат ресурсів. Нехай роблять два продукти з трьох ресурсів, випуски рівні х і у, а витрати дорівнюють т, п і k, тоді варіант виробництва має вигляд вектора:

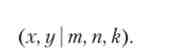
З двох варіантів виробництва більш ефективним за Парето вважають той, у якого випуски всіх продуктів не менше, а витрати всіх ресурсів не більше, ніж в іншого варіанта. Якщо у когось варіанта виробництва існує більш ефективний варіант, то він Парето-неефективний, а якщо його не існує, то він Парето-оптимальний. Сутність критерію Парето висловлює афоризм: «Краще бути багатим і здоровим, ніж бідним і хворим», т. Е. Один варіант виробництва повинен перевершувати інший варіант по всім параметрам. Особливість методу - існування пар варіантів, які годі порівняти за критерієм Парето, т. Е. Парето-оптимальний варіант не єдиний.

приклад

Розглянемо три варіанти виробництва:

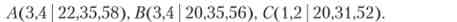
порівняємо варіанти А і В: їх випуски рівні, а витрати ресурсів у варіанту В не більш, ніж у А, тому варіант А неефективний. варіанти В н З непорівнянні, так як у випадку В випуски більше, але і витрати більше, ніж у С. Отже, В і З оптимальні за критерієм Парето.

Теорія ігор грає важливу роль в сучасній макроекономіці: в ній критерій Парето використовується для виявлення свідомо невигідних стратегій поведінки. В ігровій матриці кожний рядок відповідає стратегії «білих», а стовпець - стратегії «чорних». Елемент матриці на перетині двох стратегій дорівнює виграшу (програшу) гравців: якщо він позитивний, то «чорні» віддають цю суму грошей «білим», якщо негативний, то навпаки.

Стратегія гравця очевидно невигідна і тому не реалізується, якщо є домінуюча стратегія, для якої виграш не менше за будь-якої стратегії іншого гравця. Іншими словами, домінуюча стратегія ефективніше за критерієм Парето, ніж дана. Для «білих» все елементи домінуючою рядки не менше, ніж у цього рядка, а для «чорних» все елементи домінуючого стовпчика не більш, ніж у даного стовпчика. Якщо кожен гравець має рівно по одній Парето-оптимальної стратегії, то відповідний елемент матриці називають сідловою: якщо один гравець слід седловой стратегії, а інший вибирає іншу стратегію, то останній несе втрати. Гра справедлива, якщо седловой елемент дорівнює нулю. Сідлова точка існує, якщо максимум з мінімумів по рядках (максимин) дорівнює мінімуму з максимумів за стовпцями (минимакс).

приклад

Задана ігрова матриця:

У ній є сідлова точка, так як другий рядок домінує над іншими рядками, а третій стовпець - над іншими стовпцями. Відповідні стратегії гравців оптимальні. Максимин дорівнює мінімаксу і дорівнює 4, т. З. гра стане справедливою (сідловий елемент стане нульовим), якщо всі елементи матриці зменшити на 4.

1. Моделі безробіття, модель пошуку відповідників
   Залежність чисельності найманих в одиницю часу працівників від чисельності безробітних і кількості вакансій, або функція відповідності, може бути встановлена статистичними методами на основі фактичних параметрів ринку праці. За допомогою даної функції можна визначити характеристики стаціонарного
2. Модель глобального рівноваги
   Узагальнимо найпростішу кейнсіанську модель рівноваги на випадок глобальної економіки. Аналогом доходу країни (ВВП) тут служить вектор, що складається з доходів всіх країн, а аналогом граничної схильності до заощадження - матриця, що характеризує норму заощадження в кожній країні і інтенсивність
3. Модель динаміки безробіття
   Передбачається, що граничні витрати найму одного робочого (МС) прямо пропорційні кількості найнятих працівників в одиницю часу (/ г), оскільки при збільшенні числа вакансій зазвичай зростає їх різноманітність і складність встановлення відповідності між працівниками і робочими місцями. Крім
4. Модель ad-as і економічна політика
   В результаті вивчення матеріалу даного розділу студент повинен: знати вплив основних інструментів макроекономічної політики на основні макроекономічні показники (ВВП, інфляція та безробіття) в короткостроковому, проміжному і довгостроковому періоді; відміну інфляції попиту від інфляції пропозиції;
5. Міжнародний бізнес, світові ринки і конкурентоспроможність національної економіки, транснаціональні компанії і банки - головні актори глобальної економіки
   В результаті вивчення даного розділу студент повинен: знати ключові чинники конкурентоспроможності національної економіки; вміти аналізувати галузеву і регіональну структуру світових ринків; володіти навичками дослідження міжнародного бізнесу та його ролі в національній економіці. Актуальні
6. Методологічні принципи побудови системи таблиць «витрати - випуск»
   Таблиці «Витрати - Випуск», будучи невід'ємною частиною системи національних рахунків (СНР), являють собою сукупність взаємопов'язаних таблиць, що містять докладні характеристики виробництва та використання товарів і послуг, а також доходів, що формуються в процесі виробництва. В основі схеми
7. Методи економічних досліджень
   Кілька принципових аспектів визначають успіх дослідницької діяльності в галузі національної економіки: мова йде про цілісному підході до об'єкта вивчення. Розглядаються різні сторони будь-якого явища або процесу, виявляються різні взаємозв'язку і взаємодії учасників процесу; відбувається активне
8. Мала відкрита економіка з досконалою мобільністю капіталу
   Очевидно, що оскільки реальна ставка відсотка є «ціною» на ринку капіталу, при відсутності бар'єрів і при відсутності можливості вплинути на ставку відсотка (наприклад, за рахунок впливу на значну частину ринку позикових коштів) реальні ставки відсотка між країнами будуть вирівнюватися. Якщо