Теорія портфеля: загальний випадок

Розглянемо моделі інвестиційного портфеля з будь-якою кількістю видів акцій.

Модель 1. Розглядається задача мінімізації ризику портфеля (s²) Без урахування його прибутковості. Обмеження на компоненти портфеля мають вигляд

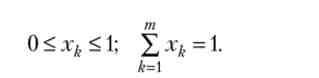
Дане завдання квадратичного програмування має два види рішень: внутрішнє і кутовий. Для кутового рішення хоча б одне нерівність перетворюється в рівність, а для внутрішнього рішення все нерівності строгі. На практиці зазвичай реалізується внутрішнє рішення, що представляє собою рішення задачі мінімізації функції ризику s² за умови рівності одиниці суми компонент портфеля. Функція Лагранжа має вигляд:

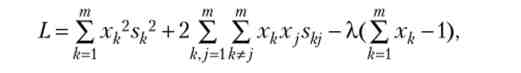
де X - множник Лагранжа.

Прирівнявши нулю її приватні похідні, одержимо систему лінійних рівнянь в матричному вигляді: А X = В. Вона має т + 1 невідомих - компонентів шуканого оптимального рішення:

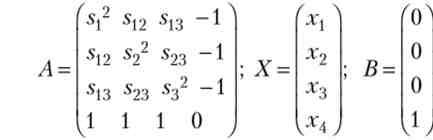
матриця А є блокової, її блок розмірності т х т є симетричною матрицею, у якій на головній діагоналі розташовані ризики (дисперсії прибутковості) акцій, а поза нею - ковариации. Для з'ясування сенсу змінної х₄ (у загальному випадку - х_{гп + 1}) помножимо перше рівняння системи на х_{, друге - на х₂, третє - на лг₃, потім отримані рівності складемо. Звідси х_А одно мінімального ризику портфеля, тому:

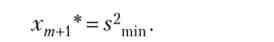
позначимо: С = А ~^{, тоді Х = С? В. З огляду на вид вектора В, робимо висновок, що координати оптимального портфеля і його ризик утворюють останній стовпець матриці З:

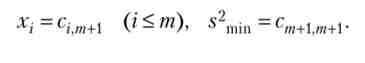
приклад

Прибутковості акцій першого виду - 4,3,4,5; другого - 5,5,4,2; третього - 2,1,5,4. Тоді дисперсії (ризики) рівні 0,5; 1,5 і 2,5, ковариация доходностей акцій першого і другого видів дорівнює -0,75 і т. Д .:

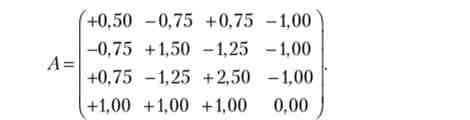
Вирішимо систему рівнянь за допомогою функцій МОБР і МУМНОЖ програми Excel (табл. 3.5).

Розрахунок оптимального портфеля: дохідність не задана

Таблиця 3.5

Оптимальний портфель - (0,627; 0,360; 0,013), його ризик дорівнює 0,053, що істотно менше ризику найменш ризикованих акцій: 0,053 < 0,5, його прибутковість дорівнює 3,987.

Модель 2. Розглядається задача мінімізації ризику портфеля з необхідною прибутковістю R₀. Тоді функція Лагранжа приймає вигляд:

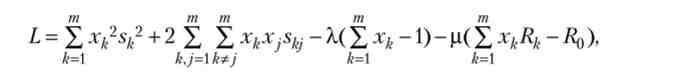
де р.- другий множник Лагранжа.

Прирівнявши нулю її приватні похідні, одержимо систему рівнянь А-Х = Вст + 2 невідомими:

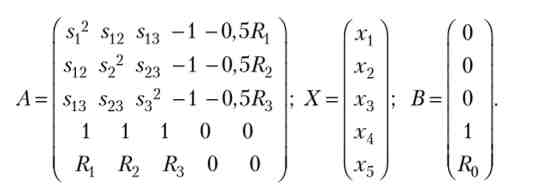
Помножимо перше рівняння на х_х, друге - на х₂, третє - на х₃, потім рівності складемо, звідси мінімальний ризик портфеля дорівнює:

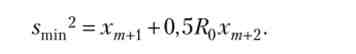
позначимо С- Л "¹, тодіХ = С В. З огляду на вид вектора В, робимо висновок, що компоненти оптимального портфеля рівні:

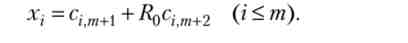
приклад

Використовуючи дані з прикладу до моделі 1, визначимо оптимальний портфель, якщо необхідна прибутковість дорівнює 3,9%. доповнимо А п'ятим рядком (4; 4; 3; 0; 0) і п'ятим стовпцем (-2; -2; -1,5; 0; 0). вектор В = (0; 0; 0; 1; 3,9). звернемо матрицю А (Табл. 3.6).

Таблиця 3.6

Розрахунок оптимального портфеля: дохідність задана

Оптимальна частка акцій першого виду дорівнює = -4,21439 + 3,9 - 1,214286 = 0,521, аналогічно: х₂ = 0,379; х₃ = 0,1; х₄ = 0,516; х₅ = -0,232. Ризик портфеля: s²min = 0,516 + + 0,5 - 3,9 - (-0,232) = 0,064. Отже, вимога забезпечити задану прибутковість призвело до збільшення ризику портфеля з 0,053 до 0,064, при цьому частка акцій першого виду знизилася з 62,7% до 52,1%.

В обох моделях завдання оптимізації зазвичай не має внутрішнього рішення, якщо дисперсія прибутковості (ризик) деяких акцій менше, ніж ковариация їх прибутковості з будь-яким іншим видом акцій. В цьому випадку пару акцій з високою кореляцією розглядають як один вид акцій і перед виконанням алгоритму оптимізації виключають з розгляду один з видів акцій, і тоді в першому блоці А кожен діагональний елемент (ризик) буде максимальним у своєму рядку і своєму стовпці. Негативні значення коваріації, що перевищують по модулю дисперсію, не виключаються, а вітаються, оскільки дозволяють істотно знизити ризик портфеля.

1. Висновки до розділу
   1. У центрі уваги економічної політики уряду в ринковій економіці знаходяться темп інфляції, рівень доходу і тісно пов'язаний з ним рівень безробіття. Тому зазвичай цільова функція залежить від цих двох показників і при цьому вона містить суб'єктивний параметр відносної значущості факторів
2. Висновки до розділу
   1. Характер циклічних процесів в економіці залежить від безлічі різноманітних причин: споживчої поведінки домогосподарств, реакції інвесторів на зміну доходу, впливу грошового ринку і політики центрального банку, переваг домогосподарств і фірм щодо споживання та інвестування, правил і умов
3. Висновки до розділу
   1. Поведінка споживача моделюють за допомогою цільової функції корисності і декількох обмежень. Аргументами цільової функції служать обсяги споживання в різні періоди часу. Їх число дорівнює двом в найпростішому випадку, а якщо їх нескінченно багато, то значення цільової функції являє собою
4. Вимір змін якості в часі
   Товари та послуги, а також умови, в яких вони реалізуються, безперервно змінюються в часі, при цьому деякі товари або послуги йдуть з ринку, а нові товари або послуги замінюють їх. Розробники національних рахунків використовують дезагреговані індекси цін, щоб Дефлірованние зміни вартості споживання
5. Відображення технічного прогресу в моделях економічного зростання, екзогенний технічний прогрес
   Поняття технічного прогресу включає всі фактори, які або збільшують випуск при заданих обсягах використання праці і капіталу, або дозволяють зробити заданий обсяг благ з меншими витратами факторів виробництва. На відміну від традиційних «речових» факторів виробництва технічний прогрес постає
6. Вибір методу., змішані методи
   Існує чотири основні варіанти складання матриці «Витрати - Випуск». Нижче наведені ці варіанти. Варіант 1. «Продукт на продукт» на основі припущення про технологію виробництва продукту. Варіант 2. «Продукт на продукт» на основі припущення про технологію виробництва в галузі; Варіант 3. «Галузь
7. Валовий внутрішній продукт
   Валовий внутрішній продукт - це ринкова вартість усіх товарів і послуг для кінцевого споживання, вироблених на території даної країни за певний проміжок часу. Слід звернути увагу на такі основні моменти. По-перше, ВВП являє собою «ринкову вартість», т. Е. Це вартісний показник, що вимірюється
8. Учасники макроекономічних відносин
   В результаті вивчення матеріалу дайной глави студент повинен: знати : поняття репрезентативного агента в макроекономіці; основні властивості функції споживання, виробничої та інвестиційної функцій; поняття межчасовий оптимізації на прикладі рішення задачі споживача; сутність гіпотези життєвого