Споживач як продавець: динаміка запасу

Валовий і чистий попит на товар

До сих пір ми припускали незалежність доходу споживача. Вважалося, що гроші на споживання у індивіда є і його завдання полягає лише в розподілі цієї суми оптимальним чином. Але звідки споживач бере гроші?

Один з варіантів відповіді на дане питання, який ми проаналізуємо в даному параграфі, - це наявність запасу благ у індивіда. Так як під запасом благ можуть розумітися будь-які можливості людини (спадщина, робоча сила, прибутковість акцій і облігацій, авторські гонорари і т. д.), А не тільки товари і послуги, пропонована модель поведінки індивіда має загальним характером і може застосовуватися до дослідження самих різноманітних ситуацій.

Нехай людина прагне до максимізації свого добробуту в вигляді максимізації функції корисності в світі двох товарів (Хі У). Індивід в своєму розпорядженні певний початковим запасом благХі Уразмере W: (X^w, У^1У). Витрати споживача на товари X і Y - це, як і раніше, сума грошей, яку він може витратити на ринку заради придбання даних продуктів в бажаних кількостях: P_x X + P_Y- Y. Ринкові ціни не залежать від дій покупця і задаються загальною економічною ситуацією в галузі. А що ж тепер є доходом споживача? Дохід індивіда - це сума грошей, яку він може виручити на ринку, якщо продасть свій первісний запас: I = Р_х ? X^w + P_Y -Y^w. Звичайно, споживач не може витратити більше грошей, ніж максимальна вартість його запасу.

Сформулюємо нову задачу вибору споживача - максимізувати корисність: тах [/ (Х, У) при наявності початкового запасу: W: (X^й', У "') і обмеження на витрати: Р_х ? X + P_Y Y = Р_х ? X^w + P_Y - Y^w.

Зауважимо, що тепер значення X і У не обов'язково повинні бути позитивними. Оптимальні кількості товарів X і У можуть бути як позитивними, так і негативними. Невід'ємні значення обсягу означатимуть покупки товару, а негативні - його продажу.

Проаналізуємо графічне рішення даної задачі (рис. 8.14).

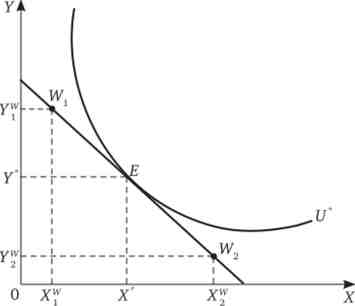
Мал. 8.14. Вибір споживача з урахуванням наявності початкового запасу

Рівновага індивіда знаходиться в точці Е, де він набуває свій оптимальний набір (X ", У *). Припустимо, що для двох споживачів цей набір в точці Е є однаково оптимальним. Однак дії індивідів для придбання даного набору будуть різними.

Перший споживач має початковим набором W, (лівіше точки Е). У цьому наборі товар У представлений в більшій кількості, ніж бажано для споживача (У) " ' > У), а товари менше, ніж би йому хотілося (Xj^W < X). Цей індивід буде продавати товар У і купувати товар X.

Другий споживач має запас у розмірі W₂ (Правіше точки Е). Тут товар X представлений в більшій кількості, ніж це потрібно даному індивіду (Xf > X), а товару У в первісному наборі недостатньо в порівнянні з оптимумом (Y ™ > У). Тому дана людина буде продавати товар X і купувати товар У.

назвемо валових попитом той обсяг товару, який в підсумку всіх ринкових угод виявиться в оптимальному споживчому наборі індивіда, а чистим попитом - різницю між валовим попитом і обсягом первинного запасу.

Валовий попит: обсяги (X *, У).

Чистий попит: X^D = X * -X^lv і y^D = Y'-Y^w.

якщо Х ° > 0 іліX > X^w, індивід є чистим покупцем товари.

Якщо Х ° < Про або X ' < X^w, то індивід є чистим продавцем товарах.

Питання для роздумів

Доведіть, що в світі двох товарів якщо ДХ > 0, то обов'язково ДУ < 0. Який економічний сенс цього твердження?

Таким чином, перший індивід виявиться чистим продавцем товару Y і чистим покупцем товару X, а другий індивід наооборот. Для індивіда, у якого Е = W, не існує проблеми купівлі-продажу. Така людина вже знаходиться в точці оптимуму, і йому немає необхідності що-небудь міняти в своєму первісному запасі. Ця людина «втрачений» для ринку.

Завдання, що ілюструє теорію

Для Саші функція корисності товарного набору дорівнює U = X¹'³ ? Y²'³. Відомо, що його початковий набір становить (Х = 5, Y = 2). Чому рівні попит і пропозиція кожного товару для Саші при цінах Р_х = 10 руб., Р_у = 25 руб.?

Рішення

Якщо Саша продасть свій початковий набір, то максимальна сума грошей, яку він виручить, буде дорівнює: 1 = 5? 10 + 2 - 25 = 100 руб.

Оптимальний вибір Саші визначається Маршалліанскімі функціями попиту. Уподобання представлені функцією Кобба - Дугласа, для якої Маршал- ліанскіе функції попиту (валового попиту) рівні

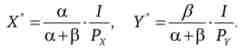
Звідки знаходимо валовий попит (підсумковий набір) Саші у * ¹⁰⁰ ч ч

^{х =}1 ^ Г³'^{3 шт}-^:

. 2100

Y = --- = 2,7 шт.

3-25

Чистий попит дорівнює:

Х ° = АХ = 3,3 - 5 = -1,7 шт .;

Y^D = AY = 2,7 - 2 = +0,7 шт.

Таким чином, Саша є чистим покупцем товару Y і чистим продавцем товарах.

1. Взаємозамінні товари, взаємодоповнюючі товари
   Взаємозамінні товари задовольняють одну і ту саму потребу індивіда. Тому раз з точки зору корисності товари рівнозначні, для покупця головним критерієм вибору стає ціна. Купується той товар, ціна якого відносно нижчою. Другий товар не купується. при MRS = 1 Перші два випадки характеризують
2. Взаємодоповнюючі товари (вчинені комплементи)
   Такі товари - це товари, які споживаються разом і в постійній пропорції: стілець і стіл; права і ліва рукавички; фотоапарат і фотоплівка, плеєр і дві батарейки. Корисність споживача приносить тільки набір з певними пропорціями. Тому функція даного товарного набору записується в такий спосіб:
3. Властивості непрямої функції корисності
   2. Непряма функція корисності неперервна за цінами і доходу. Це випливає з безперервної природи грошей, ми можемо оцінювати товари і дохід до як завгодно малої величини рахункова одиниця. 3. Непряма функція корисності є зростаючою по доходу (внаслідок аксіоми про ненасищаемості) і не зростаючої
4. Витрати довгострокового періоду
   У довгостроковому періоді всі витрати стають змінними. Різниця між сукупними і змінними витратами, таким чином, зникає. Постійних витрат більше немає. Довгостроковий період можна представити у вигляді послідовності декількох короткострокових періодів. При послідовному збільшенні постійного
5. Відсутність ринку: вільне благо, рівновагу при відсутності товару, не-єдиність рівноваги
   У даній ситуації пропозиція завжди як би «випереджає» попит при будь-яку ціну товару (рис. 3.9). Коли запаси товару перевищують потребу в ньому, навіть при нульовій ціні, ми маємо справу з вільним благом. Тут ринку не існує, оскільки споживач не готовий оплачувати те, що є в наявності в надлишку.
6. Види інвестиційних проектів
   Правильність відбору залежить від виду інвестиційного проекту. 1. незалежний проект : ? відхилення або прийняття даного проекту не впливає на прийняття рішення по іншим проектам; ? може здійснюватися як окремо, так і одночасно з іншим; ? оцінюється самостійно. 2. взаємовиключний проект : ?
7. Цінове лідерство
   Нехай тепер фірма-лідер приймає рішення щодо ринкової ціни, а фірма-послідовник, дотримуючись ціни лідера, вибирає для себе оптимальний обсяг продажів, керуючись стратегією ценополучателем конкурентного ринку. Така модель має назву «Цінове лідерство», або «Домінуюча фірма» (Модель Форхаймера
8. Тотожності еластичності
   Рівняння Слуцького не завжди легко використовувати в практичних цілях. На основі рівняння Слуцького і бюджетного обмеження споживача економісти розробили кілька інструментів, що дозволяють вирішувати господарські завдання розподілу доходу і реакції індивідів на динаміку різних економічних