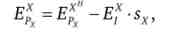
| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Рівняння Слуцького не завжди легко використовувати в практичних цілях. На основі рівняння Слуцького і бюджетного обмеження споживача економісти розробили кілька інструментів, що дозволяють вирішувати господарські завдання розподілу доходу і реакції індивідів на динаміку різних економічних факторів. Вони отримали назву «тотожності еластичності».
1. У рівняння Слуцького додамо елементи, необхідні для отримання значень еластичностей товарів:
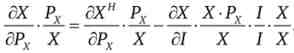
Звідки отримуємо перший тотожність еластичностей
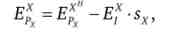
де? * - цінова еластичність Маршалліанского попиту; Е * " - цінова еластичність компенсованого попиту; Е? - еластичність попиту р. х
по доходу; sx = --частка витрат споживача в його бюджеті, яка припадає на товар X.
2. Розглянемо бюджетне обмеження в такому вигляді:
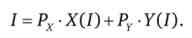
Знайдемо повний диференціал бюджетного обмеження
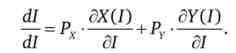
Додамо до правої частини елементи, необхідні для отримання відповідних еластичностей, але так, щоб загальний вираз не змінилося:
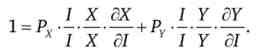
Звідки отримуємо другий тотожність еластичностей
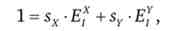
де sx і sy - частки в бюджеті споживача, що припадають на товари X і У; Ef - еластичність попиту за доходом на товар X; EJ - еластичність попиту за доходом на товар Y.
3. Розглянемо бюджетне обмеження, в якому обсяги товарів представлені Маршалліанскімі функціями попиту: I = Px-X (Px,PY,I) + + Руприхх, Ру, П.
Визначимо, яким чином змінюється бюджетне обмеження при зміні ціни одного товару (наприклад, товару X) і незмінній ціні іншого:
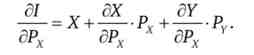
Додамо до правої частини виразу елементи, необхідні для отримання відповідних еластичностей, але так, щоб загальний вираз не змінилося.
Крім того, згадаємо, що бюджет споживача (ліва частина виразу) не змінюється під дією ціни. Тому = 0.
В результаті отримуємо х
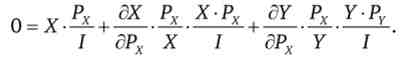
Звідки випливає третє тотожність еластичностей
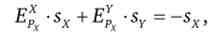
де Ерх - пряма цінова еластичність попиту на товар X; EYPx - перехресна цінова еластичність попиту на товар Y; sxnsY - частки в бюджеті споживача, що припадають на товари X і Y.
ШПАРГАЛКА
тотожності еластичності
Завдання, що ілюструють концепцію
Завдання № 1. Еластичність попиту за доходом на їжу для споживача дорівнює 1. На неї він витрачає 5% свого доходу. Еластичність попиту за ціною на їжу для нього дорівнює (-0,2). Яку величину становить цінова еластичність компенсованого попиту?
Рішення
На основі тотожностей еластичності ми знаємо, що
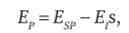
де Ер - цінова еластичність попиту; Е$ р - цінова еластичність компенсованого попиту; Е; - еластичність попиту за доходом; s - частка витрат на даний товар в сукупних витратах споживача.
Підставляючи конкретні значення: -0,2 = Esp - 1 - 0,05, отримуємо Esp = 0,15. Компенсований попит на їжу є нееластичним.
Завдання № 2. Споживач витрачає 30% свого доходу на мінеральну воду і 70% на сосиски. Еластичність попиту за доходом на сосиски дорівнює 0,2. Чому дорівнює еластичність по доходу на мінеральну воду?
Рішення
Тотожність еластичності передбачає, що:
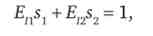
де Еп і Е12 - еластичність попиту за доходом відповідно на мінеральну воду і сосиски; s, і s2 - частки, в яких дохід споживача витрачається на перший і другий товар.
Підставляємо вихідні дані і отримуємо: 0, З-Іп + 0,7 - 0,2 = 1, звідки Еп = 2,87.
Попит на мінеральну воду досить еластичний по доходу.
Завдання № 3. Споживач витрачає половину свого доходу на хліб і половину на вино. Цінова еластичність хліба дорівнює (-0,5). Чи може цінова перехресна еластичність вина бути рівною 0,8?
Рішення
Для відповіді використовуємо ще одне тотожність еластичності:
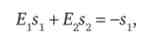
де Ej - цінова еластичність хліба; Е2 - перехресна цінова еластичність вина; Sj і 5 - частки, які споживач витрачає відповідно на хліб і вино. Підставляємо вихідні дані і отримуємо: (-0,5) - 0,2 + 0,8 - 0,2 = -0,1 + 0,16 = = 0,06 < 1.
Тотожність не виконується, отже, перехресна еластичність для вина не може складати 0,8. Щоб тотожність мало місце, перехресна еластичність вина повинна бути рівною 5,5.