Який попит на страховку?

Вартість майна (дохід) індивіда при успішному результаті і придбанні страхового поліса дорівнює: I * -aq. Вартість майна індивіда при несприятливому розвитку подій з урахуванням страхового відшкодування складе

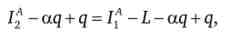
де L - вартість збитку.

Ця лінія визначає бюджетне обмеження індивіда, що робить вибір в умовах невизначеності і ризику, з урахуванням можливості придбання страхового поліса. Індивід, не схильний до ризику, хотів би бути впевненим в отриманні однакового доходу незалежно від результату. На графіку це є дохід Г.

Оптимальний вибір індивіда визначається точкою максимуму функції очікуваної корисності

В силу угнутості функції очікуваної корисності для не схильну до ризику індивіда точка локального максимуму буде і точкою глобального максимуму.

Умова першого порядку для даної функції складе

Оскільки індивід не схильний до ризику, то оптимальна величина q не може бути рівною нулю.

Якщо ринок страхових послуг є конкурентним, то прибутку страхових компаній в довгостроковій перспективі будуть прагнути до нуля, т. Е.

Страхова компанія отримує виручку від продажу страхового поліса в розмірі щ і виплачує страхове покриття в розмірі q з ймовірністю (1 - р).

Така страховка виявиться актуарно справедливої - вартість одиниці страховки дорівнюватиме ймовірності настання страхового випадку: а = (1 - р).

У разі актуарно справедливої страховки

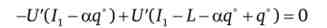
або

де q - оптимальний обсяг страхового покриття, на який пред'являє попит індивід, не схильний до ризику.

В силу суворої увігнутості і зростання функції очікуваної корисності похідні рівні тоді і тільки тоді, коли рівні аргументи функції

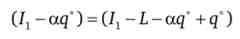
або q = L. Оптимальний обсяг страхового покриття відповідає повною величиною очікуваного збитку. Індивід буде купувати повну страховку.

Добробут індивіда покращився. Оптимум досягнутий в точці Е при більш високому рівні очікуваної корисності EU_r

Зауважимо, що в реальності страховка не є актуарно справедливою: страхові компанії несуть поточні витрати (крім виплат за страховими полісами); ринок страхування не завжди конкурентний; страхові компанії враховують проблему інформаційної асиметрії, в результаті якої можуть змінюватися ймовірності виплат для деяких категорій індивідів.

Завдання, що ілюструє концепцію

пан N планує закордонне турне, в якому він збирається витратити 10 000 євро. Його корисність від турне визначається тією кількістю грошей, які він фактично витрачає: L / (/) = V7 (де I - витрачені гроші). Відомо, що ймовірність втрати 1000 євро становить 25%. Чи захоче пан N купити повну страховку від втрати за 250 євро? Яку максимальну суму він готовий заплатити за повну страховку?

Рішення

Очікувана корисність турне в разі, якщо пан N не набуде страховку, складе

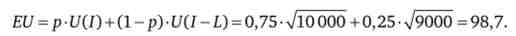
Повне покриття збитків при настанні страхового випадку виявиться рівним Зі страховкою корисність турне буде дорівнює

пан N готовий заплатити за страховку не більше тієї величини, яка вирівнює корисність турне в двох випадках: зі страховкою і без неї. Це рух індивіда уздовж однієї і тієї ж кривої байдужості.

Звідки знаходимо максимальну ціну страховки

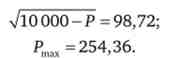
Таким чином, максимальна сума, яку пан N готовий заплатити за позбавлення його від ризику, становить 254 євро. Тому при ціні страховки в 250 євро він обов'язково її придбає.

1. Ефект доходу і ефект заміни по Слуцькому
   Коли ціна товару змінюється, споживач стикається з двома явищами. По-перше, змінюється його реальний дохід, т. Е. Купівельна спроможність наявних у нього грошей. По-друге, варіює відносна ціна всіх інших товарів, які входять до споживчого набору індивіда. Економісти виділяють два самостійних
2. Двоїста задача в теорії споживчого вибору, вибір споживача з метою мінімізації витрат
   Мистецтво полягає в тому, щоб знайти незвичайне в звичайному і звичайне в незвичайному. Дені Дідро, французький філософ XVIII ст. Після вивчення цього розділу студенти будуть: знати особливості двоїстої задачі споживчого вибору; вміти доводити і використовувати в дослідженнях лемму Шепарда
3. Дослідження еластичності на практиці
   Для того щоб оцінити ступінь еластичності попиту, було проведено опитування керівників російських підприємств. У числі інших керівників ставив перед собою такої питання: «Якщо ви сьогодні підвищите ціни на основну продукцію вашого підприємства на 10%, то як, на вашу думку, це вплине на обсяг
4. Державне регулювання ринку: «стелю» і «стать» цін, введення «стелі» цін (максимальної ціни)
   Навіть якщо всі умови стабільного і єдиного рівноваги виконуються для галузі, це не означає автоматично, що дане рівновагу дійсно буде реалізовано. У діяльність ринку може втручатися держава. Втручання держави приймає найрізноманітніші форми. Почнемо з найбільш простого і найбільш поширеного
5. Чому вчить ця глава
   У цьому розділі були показані різні варіанти вимірювання добробуту споживача. Коли змінюються ціни товарів і (або) номінальний дохід індивіда, слід очікувати зміни його добробуту. У державній політиці на підставі даних наслідків можна зробити висновок про те, наскільки істотно відіб'ється
6. Чому вчить ця глава, контрольні питання, вправа для самостійної роботи
   Дана глава показує, що якщо в галузі діє кілька великих фірм, то їх поведінка виявляється стратегічним - фірми беруть до уваги очікувану реакцію конкурента на свої дії. Виникає взаємна залежність фірм друг від друга, яку вони добре усвідомлюють. Стратегічне поведінка може виражатися у вигляді
7. Чому вчить ця глава, контрольні питання
   У цьому розділі було проаналізовано вибір споживача. Ми побачили, що максимізація власного добробуту з боку індивіда може бути формалізована в якості математичної задачі досягнення умовного максимуму функції корисності при наявності бюджетного (і в деяких випадках тимчасового) обмеження споживача.
8. Благо і антиблаго
   Деякі товари можуть викликати негативні наслідки для здоров'я споживача або суб'єктивно не подобатися індивіду. Товари подібного роду називаються антиблаго. Збільшення споживання антиблаго призводить не до зростання, а до скорочення сукупної корисності товарного набору. Прикладами наборів