| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Мистецтво полягає в тому, щоб знайти незвичайне в звичайному і звичайне в незвичайному. Дені Дідро, французький філософ XVIII ст.
Після вивчення цього розділу студенти будуть: знати
володіти
- навичками порівняння компенсованого і некомпенсованого попиту. У попередньому розділі ми розглядали проблему вибору споживачем оптимального набору з точки зору максимізації сукупної корисності товарів при бюджетному обмеженні, заданому ззовні. Але часто буває так, що споживачеві доводиться вирішувати іншу задачу - вибирати мінімальний за вартістю набір, який міг би принести йому корисність не нижче якоїсь наперед визначеної величини.
Нехай споживач хоче досягти рівня добробуту, представленого кривої байдужості U " (Рис. 7.1). Лінії витрат З|; З2, З3 показують різні вартості наборів, що складаються з товарів, що цікавлять споживача.
Лінії витрат паралельні один одному, оскільки вони відображають різні вартості споживчого кошика при одних і тих же цінах одиниць товарів. Кожна лінія витрат може бути записана у вигляді бюджетного обмеження з різним рівнем бюджету: С, = Рх X + PY Y.
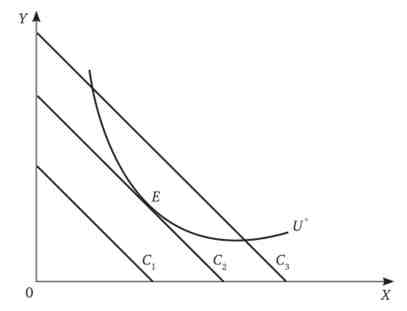
Мал. 7.1. Мінімізація витрат споживача
Подивимося уважно на рис. 7.1. лінія Зх проходить нижче цільового рівня добробуту. Отже, витрати тут найменші, але вони не дозволяють придбати товарний набір з бажаної сукупною корисністю. лінія З3 дозволяє купити набір, який задовольнив би шукане обмеження, але витрати в даному випадку не будуть мінімальними. Зменшивши витрати до лінії С2, споживач отримає набір Е, який задовольняє двом умовам: рівень корисності відповідає бажаному; витрати мінімальні. Це і буде оптимум споживача.
Для аналітичного рішення задачі мінімізації витрат при заданому рівні корисності скористаємося методом Лагранжа.
Нехай для визначеності переваги споживача представлені функцією Кобба - Дугласа: U (X, У) = Х " ? У5.
Потрібно вирішити задачу мінімізації: З = Рх-Х + Py-Y при U - Xй ? У11 = 0.
Складаємо функцію Лагранжа: Lag = Рх- X + Ру - У - X (.U - Ха ? Ур).
перед X стоїть знак «мінус», так як ми мінімізуємо витрати.
Знаходимо приватні похідні і прирівнюємо їх до нуля (умова оптимальності першого порядку)
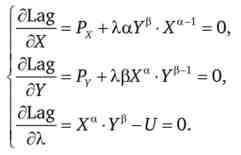
Звідки отримуємо
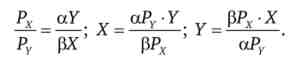
Підставляємо черзі значеннях і У в третє рівняння системи.
Знаходимо рівноважні значення X і У

Рівноважні значення обсягів придбаних товарів, як очевидно, залежать від цін товарів і рівня корисності. Залежність між ціною товару X та обсягами його покупок, як ми знаємо, носить назву «функція попиту». Однак тут у функцію попиту включається цільове значення корисності. При будь-якому рівні цін (в розумних межах) споживач буде таким чином компенсувати свої витрати, щоб завжди залишатися на одній і тій же кривій байдужості. Подібна функція попиту називається компенсованим, або Хіксіанскім, попитом.
Історична довідка
сер Джон Річард Хікс (1904-1989), англійський економіст. Лауреат Нобелівської премії 1972 р за новаторський внесок у загальну теорію рівноваги і теорію добробуту. Навчався в Оксфорді на математичну стипендію. Хоча здобув освіту як математик, цікавився також літературою та історією. Був професором Оксфордського і Манчестерського університетів, працював в Лондонській школі економіки. У 1942 р був обраний членом Британської академії наук. У 1960-1962 рр. був президентом Королівського економічного товариства Великобританії. У 1964 р ззнавств у дворянське звання. Був членом Шведської королівської академії наук, Національної академії наук Італії, членом Американської академії наук і мистецтва. Найбільш відома його книга - «Вартість і капітал». Хікс розробив математичні основи теорії граничної корисності і теорії економічної динаміки та заробітної плати.
У загальному вигляді функція Хіксіанского попиту буде виглядати наступним чином:
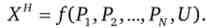
Розглянемо інший варіант вибору споживача мінімізації витрат - квазілінійну переваги: U (X, У) = v (X) + Y (Корисність лінійна по товару Y).
Вирішимо задачу мінімізації Е = Рх-Х + Py-Y при U - v (X) - Y = 0.
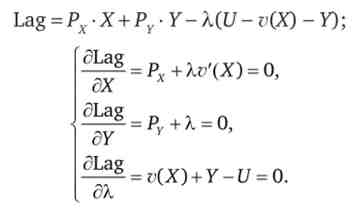
Для знаходження внутрішнього рішення (рис. 7.2, а) знову скористаємося методом Лагранжа
p (p л
Звідки v '(X) = ^ - = f (X), X * = / 1 -г-= XPx,PY).
* Y V * Y
висловимо Y з третього рівняння системи:
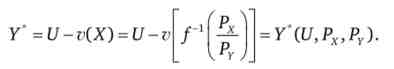
Отже, ми отримали, що в разі квазілінійних уподобань (лінійних по товару У) попит на товар X залежить від цін товарів X і У, але не залежить від рівня корисності, тоді як попит на товар У залежить і від цін товарів, і від рівня корисності. У разі квазілінійних уподобань лінійних по товару X буде спостерігатися зворотна картина.
Однак при квазілінійних перевагах може з'явитися і кутове рішення (рис. 7.2, б) (як і при скоєних субститутів). Воно справедливо тоді, коли індивідуальна норма заміщення споживача менше ринкової: покупець готовий віддати все одиниці одного товару (в даному варіанті товари) для придбання іншого (в даному варіанті товару У). При етомХ = О, У = У *, a U = v (X) + У = У *.
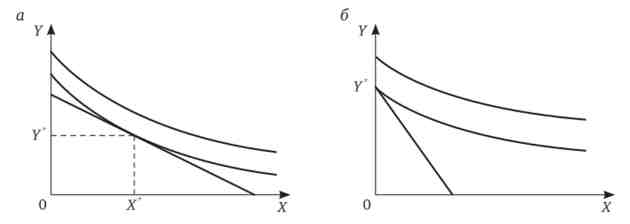
Мал. 7.2. Мінімізація витрат при квазілінійних перевагах
В разі товарів-субститутів при функції корисності виду: 1ДХ, У) = = АХ + bY вирішити задачу мінімізації витрат при заданому рівні корисності, застосовуючи метод Лагранжа, не вдасться, оскільки при даних перевагах внутрішнього рішення немає (рішення може бути тільки кутовим (рис. 7.3)).
Можливі три випадки:
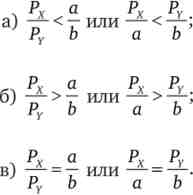
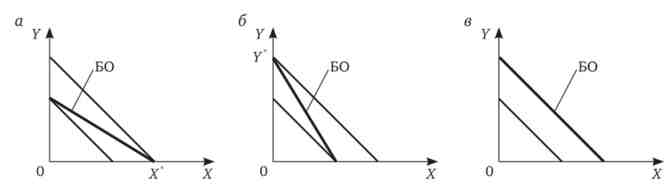
Мал. 7.3. Мінімізація витрат для товарів-субститутів:
БО - бюджетне обмеження
У разі, представленому на рис. 7.3, а, індивід відмовляється від споживання товару У (У = 0) і переключається на споживання товари (X = Х '), так як вартість товари в цьому варіанті дозволяє досягти заданого рівня корисності за меншу суму, ніж якби споживач купував товар Y. А раз товари замінюють один одного, то раціональний споживач вибирає той продукт, який за меншу суму дозволяє задовольнити його потребу.
тоді U = аХ + bY = аХ '. Звідки X "= -.
а
У разі, представленому на рис. 7.3, б, індивід відмовляється від споживання товари (X = 0) і переключається на споживання товару У (7 = У *), оскільки вартість товару У в цьому варіанті дозволяє досягти заданого рівня корисності за меншу суму, ніж якби споживач купував товар X . ц
тоді U = аХ + bY = bY Звідки У "= -
про
У разі, представленому на рис. 7.3, в, споживачеві все одно, який з товарів купувати (X або Y), так як суми, які необхідно витратити і на товар X, і на товар У для досягнення бажаного рівня корисності, однакові. Хіксіанская функція попиту збігається з лінією витрат.
для комплементарних товарів при функції корисності виду: U (X, У) = = min (aX, Ьу) коефіцієнти а і b залежать від переваг конкретного індивіда. Вони інформують нас про те, що індивід, максимізуючи корисність, вважає за краще купувати блага і У в строгій пропорції: а одиниць товари і ред одиниць товару У.
У разі товарів-комплементов метод Лагранжа, як і при товарів-субститутів, не працює, так як функція 1ДХ, У) = min (aX, Ьу) НЕ дифференцируема.
Однак можна піти іншим шляхом. З умови ми маємо: - = - або
X b
аХ = bY. Зафіксуємо рівень корисності U ' (Рис. 7.4). Цей рівень корисності нам забезпечують а одиниць товару У або b одиниць товари, т. е. U "- аХ * = bY Якщо ми почнемо змінювати корисність (зробимо її змінною величиною), то отримаємо функції попиту
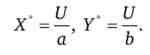
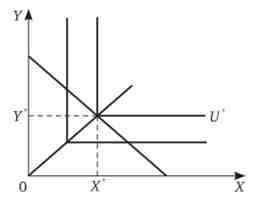
Мал. 7.4. Мінімізація витрат для комплементарних товарів
Для інших (в тому числі більш складних) видів переваг рішення задачі мінімізації витрат для досягнення бажаного рівня корисності і висновок функції компенсованого попиту можливі на основі методу Лагранжа.