| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Функція Хіксіанского попиту показує оптимальні обсяги товарів, які набуває індивід при різних цінах і різних цільових рівнях корисності. Якщо тепер в первісної лінії витрат споживача ми замінимо довільні обсяги покупок оптимальними, то отримаємо функцію витрат, яка характеризує динаміку мінімальних витрат індивіда
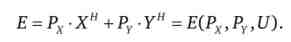
Функція витрат споживача показує рівень витрат, мінімально необхідний в наявної цінової ситуації для досягнення заданого рівня корисності, представляючи собою тим самим функцію мінімальних значень витрат від параметрів (P, U):
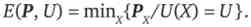
Можна знайти функції витрат для найбільш цікавих видів переваг споживача.
1. Функція витрат для стандартних переваг виду Кобба - Дугласа

Наприклад, якщо переваги Кобба - Дугласа описуються функцією: U (X, У) = X1/5Y1 / S, то функція витрат в цьому випадку має вигляд
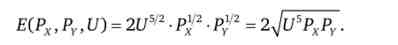
2. Функція витрат для квазілінійних уподобань при внутрішньому оптимум набуде вигляду
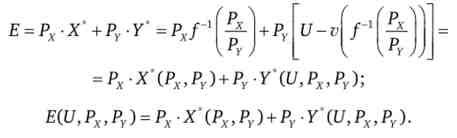
Наприклад, якщо квазілінійну переваги описуються функцією U (X, Y) = LnX + Y, то функція витрат буде дорівнює
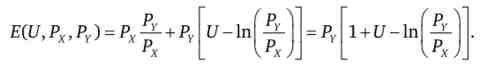
У разі кутового оптимуму функція витрат набуде вигляду: E (U, Ру) = = PyY * = PYU, якщо переваги лінійні по товару Y. Якщо переваги лінійні по товару X, то за аналогією функція витрат буде: E (U, Рх) =
= рхг = рхі.
3. Для товарів-субститутів можливі наступні варіанти функції витрат.
При оптимальному виборі придбання тільки товару X функція розподілу
Р
ходів набуде вигляду: E (U, PX) = U-.
а
При оптимальному виборі покупки тільки товару Y функція витрат
буде: E (U, PY) = U% о
У загальному вигляді маємо таку функцію витрат для товарів-субститутів
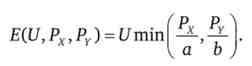
4. Підставивши отримані раніше функції Хіксіанского попиту в цільову функцію (Е = РхХ + PyY), отримаємо функцію витрат для товарів-комплементов
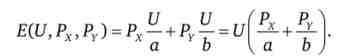
Розглянемо властивості функції витрат споживача Е (_р, U).
1. Функція витрат опукла вгору по відношенню до змінної цін. Доведемо цю властивість.
Нехай Р, і Р2 - вектори цін на ринку.
Візьмемо вектор цін Р = до Р1 + (1 - к) Рг, де 0 < до < 1.
Припустимо, що Хл і Х2 - товарні набори, відповідні мінімуму витрат споживача для досягнення певного (одного і того ж) рівня корисності при цінах Р1 і Р2, а набір X - оптимальний вибір при цінах Р.
Тоді, за визначенням функції витрат, вірні такі нерівності:
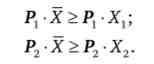
Функція витрат являє собою мінімальну вартість споживчого набору, всі інші набори не можуть бути нижче за видатками. Помножимо перша нерівність на до, а друге - на (1 - до), Тоді
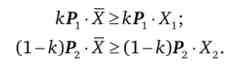
Так як до - невід'ємне число, знак нерівностей збережеться. Складемо праві і ліві частини нерівностей
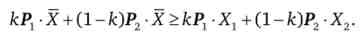
Винесемо за дужки загальний член
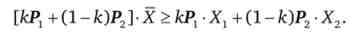
Вираз у квадратних дужках зліва одно Р. Запишемо підсумкове нерівність
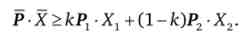
А це і є визначення опуклості (рис. 7.5).
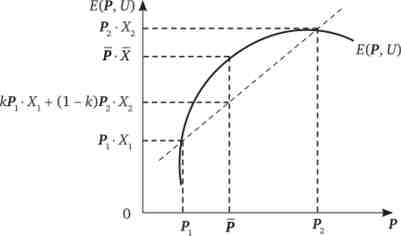
Мал. 7.5. Опуклість функції витрат по змінної цін
Питання для роздумів
Доведіть, що опуклість функції витрат по відношенню до змінної цін є наслідком нерівності функції корисності.
dE {P, U)
2. Функція витрат є неубивающей по ціні товару: - гг- ^ 0.
де (Р U)
якщо Xi > 0, --- > 0. Якщо хоча б один товар купується индиви-
8Pi
будинок, то функція витрат є зростаючою хоча б за ціною цього товару. Витрати для досягнення початкового рівня корисності зростають при збільшенні ціни хоча б одного продукту зі споживчого набору.
3. Функція витрат однорідна першого ступеня.
Нехай всі ціни збільшилися в до раз. Загальне зростання цін у однакове число раз не змінює відносних цін, які і є детермінантою споживчого вибору. Тому той же набір і в тих же обсягах задовольняє мінімальним витратам для отримання початкового рівня корисності.
якщо Е ° = Е (Р °,Ua) = Р °? X " (Всі змінні - вектори), то
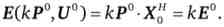
4. Функція витрат є зростаючою по змінної рівня корисності U.
При даних цінах для досягнення більш високого рівня корисності
5Е
буде потрібно більше витрат: -> 0. Ми можемо знайти цей вислів: де 1 ^
- = до2 = -, де А_2 - множник Лагранжа в двоїстої завданню, що показує граничні витрати на одиницю корисності; Х,х - множник Лагранжа в прямій задачі оптимального вибору споживача (максимізації корисності при бюджетному обмеженні).
Наступні два властивості настільки важливі, що необхідно виділити їх в окремі параграфи.