| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Ні-едінственност' в поданні переваг споживача. Уподобання споживача поряд з базовою функцією корисності можуть бути адекватно описані за допомогою монотонної трансформації функції корисності.
монотонна трансформація - таке перетворення функції корисності, яка не змінює порядок переваг (ординалистской властивості функції корисності): якщо набір А був краще набору В до трансформації, то після монотонної трансформації набір А як і раніше буде віддавати перевагу споживачем у порівнянні з набором В, незважаючи на те, що кількісне вираження корисності наборів змінилося в результаті трансформації. Тому в аналітичному плані можна працювати не з самою функцією корисності (якщо це утруднене), а з її монотонної трансформацією.
До монотонної трансформації можна віднести наступні види монотонних позитивних перетворень:
Наприклад, функції U = 0,51пХ + 0,51пУ і X = U / Y є монотонними трансформаціями функції корисності J = X - Y. функція U = yfx + 10У + 5 - монотонна трансформація функції U = 4х + У. Функції U = X2 + 2XY + У2 і U + до = [X + У]1/2 являють собою трансформацію базової функції U = X + У.
Гранична норма заміщення в споживанні (MRSз). Позначення граничної норми заміщення дано на основі перших букв англ, терміна marginal rate of substitution. Оскільки обмін одного товарного набору на інший відбувається в споживанні і характеризує суб'єктивний вибір покупця, цю норму заміщення називають граничною нормою заміщення в споживанні.
Гранична норма заміщення товару У товаром X показує, яку кількість товару У споживач готовий віддати, щоб отримати одиницю товару X, за умови, що сукупна корисність товарного набору для споживача не змінюється:
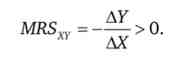
Тут чисельник (ДУ) характеризує ступінь зміни обсягу споживання товару У (яким «жертвує» споживач), а знаменник (ДХ) показує ступінь зміни споживання товару X (Який споживач отримує в обмін). Так як чисельник від'ємний (споживач «втрачає» товар, переходить від товарного набору з великим об'ємом Y до товарного набору з меншим об'ємом X), то вираз для MRS було б менше нуля. Однак економісти не люблять оперувати з негативними числами. Тому перед дробом ставиться знак «мінус». І все вираз надає позитивним!
При підрахунку граничної норми заміщення доцільно використовувати наведену нижче формулу. Так як споживач рухається уздовж однієї і тієї ж кривої байдужості з постійним рівнем корисності, замінюючи один товарний набір іншим, то аналітично це означає, що повний диференціал функції корисності споживача дорівнює нулю:
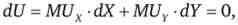
де MUX і MUY - граничні корисності товарів X і У; dX і dY - зміни обсягів споживання товарів X і Y.
Шляхом перетворень отримуємо вираз
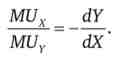
Права частина цього виразу, за визначенням, є гранична норма заміщення в споживанні, тому ми можемо записати
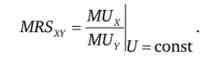
Дана аналітична формула показує, що гранична норма заміщення двох товарів в споживанні може бути виражена через відношення їх граничних корисностей.
Відзначимо важливу властивість граничної норми заміщення: MRS не змінюється в результаті монотонної трансформації функції корисності.
Доведемо це твердження.
Нехай F - монотонна трансформація функції корисності 1ЛХ, У). знайдемо MRS для функції F. Скористаємося формулою обчислення граничної норми заміщення через відносини граничних корисностей і застосуємо правила обчислення похідної складної функції (якою є функція F). Отже, отримуємо
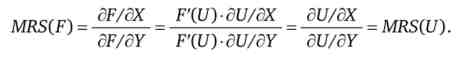
Очевидно, що після скорочення підсумкова формула граничної норми для нової і формула для початкової функцій корисності збігаються. Таким чином, ми довели, що монотонна трансформація не змінює граничну норму заміщення в споживанні.
Для гомотетічних переваг гранична норма заміщення залежить тільки від співвідношення кількостей товарів і однакова вздовж променя, що виходить з початку координат з позитивним нахилом. Всі криві байдужості в точці перетину з цим променем мають однаковий нахил, який не залежить від того, як далеко від початку координат розташовується якась крива байдужості. Властивість гомотетічності допомагає спростити аналіз поведінки споживача. Якщо переваги гомотетічни, то висновок щодо вибору індивіда, зроблений по одній кривій байдужості, буде вірним і для всіх інших кривих байдужості.
Питання для роздумів
Доведіть, використовуючи графічний і формальний аналіз, що переваги
стандартного виду, переваги для досконалих субститутів і досконалих комплементов гомотетічни, а для квазілінійних уподобань - негомотетічни.
Зменшення граничної норми заміщення в споживанні. Що відбувається в міру того, як споживач замінює товар У на нові і нові обсяги товару XI Чи залишається гранична норма заміщення постійної або вона схильна до зміни?
При русі вздовж кривої байдужості в напрямку зростання X і убування У гранична корисність товару X зменшується (відповідно до закону спадної граничної корисності) - чисельник формули, а гранична корисність У збільшується - знаменник формули. Таким обрами I
зом, -* -р - гранична норма заміщення двох товарів - убуває.
MU у т
Затвердження про убування граничної норми заміщення в споживанні еквівалентно твердженням про опуклості кривих байдужості до початку координат.
Спробуємо довести це твердження формальним чином.
Нехай функція корисності представлена у вигляді: U = U (X, Y). Так як функція корисності характеризує будь-якої однаковий рівень для декількох різних товарних наборів, ми можемо висловити обсяг споживання одного товару через обсяг споживання іншого товару, наприклад, таким чином: У = У (Х, U). Як ми знаємо, подібна монотонна трансформація не змінює уподобань споживача. Тоді початкова функція може бути записана так: U = U [X; Y (X)], де функція У = У (Х) показує, яка потрібна величина У, щоб «потрапити» на рівень корисності, відповідний конкретному значенню X. Функція корисності виявляється складною функцією. Тому гранична корисність товару X теж являє собою складне вираз
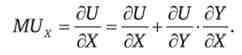
Знайдемо тепер динаміку зміни MRS.
Так як в обчисленнях нам знадобляться складні вирази для першої і другої похідних функції корисності, введемо додаткові спрощують позначення:
Ux - перша приватна похідна функції корисності по аргументуХ:
Ux = -;
* ДХ
Uy - перша приватна похідна функції корисності по аргументу У: 8Y
U у = -;
ТТ V рр 5і
Uw - друга похідна по X: U ^
ОХ
тг v рр д2і
Uyy- друга похідна по У: іп = ~ ^ '>
UXY і UYX - другі змішані частинні похідні по X і У:
,, 82jj " д2ц w DX8Y ™ DYaX
обчислимо похідну MRS по X
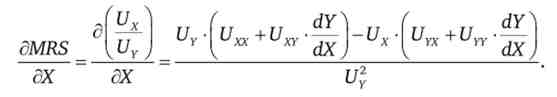
Підставами замість нову формулу MRS: Врахуємо властивість інваріантності друге змішаних похідних: = Un. після
підстановок і спрощення отримуємо підсумкове вираз
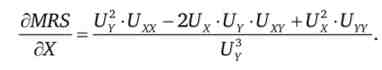
оскільки UY > 0, знак підсумкового вираження залежить від чисельника дробу. Зауважимо, що саме по собі спадання граничної корисності ще не гарантує зменшення граничної норми заміщення. хоча іух < О і іп < 0 (закон убування граничної корисності товару), для встановлення точного знака похідної MRS потрібно визначити, більше, менше нуля або дорівнює йому вираз другий змішаної похідної U ^, яка в економічному сенсі показує, як спадання обсягу споживання товару У впливає на граничну корисність товарах. Крім того, якщо цей знак негативний, потрібно встановити числове значення змішаної похідної. Тому в принципі можливий випадок, коли середній член чисельника дробу виявиться позитивним і зможе переважити негативні значення двох інших членів, так що динаміка MRS виявиться неотрицательной або навіть більше нуля.
Таким чином, більш детальне вивчення зміни граничної норми заміщення в споживанні виявляє певні складності в її динаміці і дозволяє більш точно встановити не тільки знак, але й саме значення швидкості зміни MRS.