Взаємодоповнюючі товари (вчинені комплементи)

Такі товари - це товари, які споживаються разом і в постійній пропорції: стілець і стіл; права і ліва рукавички; фотоапарат і фотоплівка, плеєр і дві батарейки. Корисність споживача приносить тільки набір з певними пропорціями. Тому функція даного товарного набору записується в такий спосіб: U (X, У) = min {aX, pT}, де a > 0; р > Про - параметри функції.

Карта кривих байдужості для взаємодоповнюючих товарів представлена на рис. 5.7.

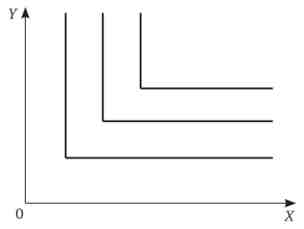
Мал. 5.7. Лінії байдужості для взаємодоповнюючих товарів

Кутові точки всіх кривих байдужості лежать на промені, що виходить з початку координат під кутом, який визначається пропорцією споживання двох товарів. У кутовій точці не спостерігається надлишку жодного

Y а

товару, т. е. аХ = Ру, отже, - = - (наприклад, один стіл і два

X р

стільця; дві сосиски і три шматочки хліба).

Для переваг цього типу, строго кажучи, неможливо знайти граничну норму заміщення в будь-якій точці на кривій байдужості, так як: 1) в кутовій точці формально не можна взяти похідні (околиця невизначена); 2) на вертикальній ділянці ліній байдужості гранична корисність товару X дорівнює нулю, а гранична корисність товару Y буде нескінченна; 3) на горизонтальній ділянці ліній байдужості гранична корисність товари буде нескінченна, а гранична корисність товару Y- дорівнює нулю. Гранична норма заміщення буде містити нуль і нескінченність.

Однак для приблизного уявлення про заміщення двох товарів можна скористатися економічним змістом даного набору. Якщо товари доповнюють один одного в споживанні, то замінити один товар на інший не представляється можливим. Тому можна вважати, що з економічної точки зору гранична норма заміщення дорівнює нулю.

Квазілінійну переваги. У низці товарних наборів корисність залежить головним чином від одного, ключового, товару (вплив якого на загальну корисність лінійно). Другий товар може додаватися або зменшуватися в невеликих кількостях без істотного впливу на сукупну корисність набору - це вплив буде нелінійним. Такі переваги відносять до квазілінійну увазі.

Приклад квазілінійних уподобань - це м'ясо і сіль (нелінійний товар); олівець (нелінійний товар) і папір; книга і закладка (нелінійний товар).

Функція корисності в даному випадку може бути представлена так: U (X, Y) = v {X) + Y. Функція корисності лінійна по товару Y, a v (X) - нелінійна її частина.

Графічне зображення дано на рис. 5.8.

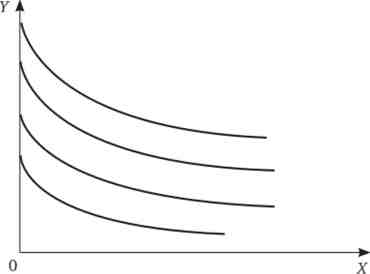
Мал. 5.8. Криві байдужості для квазілінійних уподобань

Один з варіантів економічної інтерпретації квазілінійних уподобань полягає в наступному: лінійна частина являє собою товар, який споживається в відносно великих кількостях в порівнянні з нелінійним товаром, споживання якого практично не змінюється (або змінюється порівняно незначно) при зростанні споживання лінійного товару.

Зауважимо, що кожна крива байдужості починається від осі, на якій відкладається величина товару, що змінюється лінійним чином (на графіку це товар У). Подальше спадання кривої носить нелінійний характер. Закон убування граничної корисності нелінійного товару забезпечує опуклість лінії до початку координат.

Прикладами квазілінійних функцій корисності можуть бути такі, як:

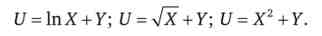
Знайдемо граничну норму заміщення.

Розглянемо таку квазілінійну функція корисності: U = v (X) + kY.

Так як гранична корисність лінійного товару постійна і дорівнює до (В окремому випадку к = 1), то гранична норма заміщення буде функцією лише однієї змінної - обсягу споживання нелінійного товару:

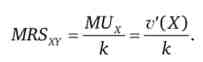
Обсяг споживання лінійного товару не впливає на граничну норму заміщення.

1. Двоїста задача в реченні праці
   До ринку праці ми можемо застосувати концепцію двоїстої задачі споживчого вибору. Нехай індивід прагне мінімізувати витрати, пов'язані з досягненням певного рівня корисності, при виборі між дозвіллям і роботою: де За лемі Шепарда: - = -L. При зростанні заробітної плати до- dw ні витрати індивіда
2. Дослідження рівноважних станів: ефект доходу і ефект заміщення, криві «ціна-споживання» і функції попиту
   В якому б положенні люди не знаходилися, вони завжди можуть знайти зручності і незручності. Бенджамін Франклін, громадський і політичний діяч США XVIII ст. Після вивчення цього розділу студенти будуть: знати особливості побудови кривих «ціна-споживання» і «дохід-споживання»; вміти знаходити
3. Дискримінація на ринку праці
   Рівновага на ринку праці, в якій би формі воно не реалізовувалося, означає встановлення єдиної для всіх працівників ставки заробітної плати. Однак в реальності ми зустрічаємо досить істотні відмінності величин грошових винагород, одержуваних працівниками за працю. Виникає питання: чому існують
4. Чому вчить ця глава
   У цьому розділі показано, що різноманітні умови галузей і ринків змушують фірми шукати оптимальні способи закупівлі ресурсів і збуту товару. Вертикальна ланцюжок руху товару від виробника до кінцевого споживача може налічувати кілька стадій і декількох контрагентів. Подібний механізм породжує
5. Чому вчить ця глава, контрольні питання, вправа для самостійної роботи
   У цьому розділі ми проаналізували загальну рівновагу в економіці з урахуванням обміну, виробництва, наявності грошей і функції колективного переваги. Було доведено, що економіка конкурентних ринків за певних умов породжує єдиний набір рівноважних цін, який є Парето-ефективним і стабільним.
6. Чому вчить ця глава, контрольні питання, вправа для самостійної роботи
   В цьому розділі показана складність такого простого на перший погляд події, як зміна ціни одиниці товару. Нерідко фірми і державні чиновники, що відповідають за соціальну політику, опиняються у складній ситуації, коли здавалося б ретельно спланована акція ціноутворення не приносить бажаних
7. Чи є рівновага в навколишньому світі, як же упевнитися, що теорія вірна?
   Теоретичні моделі ринкової рівноваги мають один суттєвий недолік: їх складно, і навряд чи можливо, перевірити на практиці. На діяльність компаній і поведінку споживачів на будь-якому ринку одночасно впливає так багато факторів, що узгодити теорію з практикою стає справою досить проблематичним.
8. Асиметрична інформація щодо ціни товару
   У деяких випадках значення має наявність або відсутність інформації про ціни товари, що пропонуються різними фірмами. Яким чином встановлюється рівновага в даному випадку, показує модель Даймонда - модель «пастка для туриста». Припустимо, що в місто приїжджає на один день турист. Він хоче