| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Доповнимо модель максимізації споживання домогосподарств сектором виробництва. Чисельність населення (L) Незмінна. Дохід (F) описується функцією Кобба - Дугласа, тоді дохід на душу населення (у = = Y / L) є функція (/) фондоозброєністю праці (k = К / L), а рівноважна ставка відсотка (г) є похідна цієї функції:
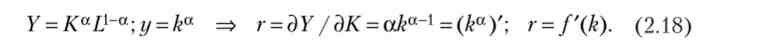
Підставами (2.18) в рівняння Ейлера для завдання максимізації корисності, враховуючи, що при постійному населенні споживання (С) і споживання на душу населення (з = З / L) ростуть рівним темпом:
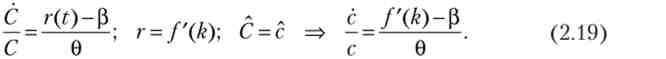
Приріст капіталу в одиницю часу дорівнює різниці доходу і споживання. Тоді приріст фондоозброєності дорівнює різниці доходу на душу населення і споживання на душу населення:
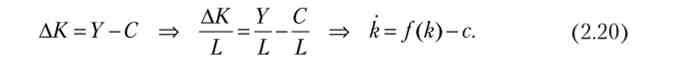
Система диференціальних рівнянь (2.19) і (2.20) описує динаміку показників k і с; її рішення називають фазовими траєкторіями. У стаціонарній точці E (k *, с *) ці показники незмінні, вона єдина і перебуває з системи рівнянь:

З (2.21) випливає, що рівноважні значення споживання, фондоозброєності і доходу залежать від норми дисконтування (р), але не залежать від параметра функції корисності (0).
У площині (доу с) перше рівняння (2.21) зображується вертикальною лінією, а друге - висхідній кривій. Стаціонарна точка є точка перетину цих ліній, які розбивають площину на чотири області. Розглянемо область Л, в якій k
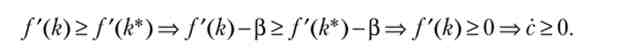
Споживання з також зростає, що випливає з формули (2.20). Аналогічно можна показати, що в області В, у якій до > до*, з / (&), Показник до зростає, з убуває. область З: k> k *7 з f (k). показники киць зменшуються. область D: k < до *, з f (k). показник до убуває, з зростає. В областях Л і С показники до і з змінюються в напрямку від стаціонарної точки, а в областях В і D - в напрямку до неї. Таким чином, стаціонарний стан нестійкий. Для будь-якого початкового значення / е0 існує таке початкове значення за0, що існує приватна рішення системи (2.19) і (2.20), що проходить через точку (&0, з0) І стаціонарну точку еу - його графік називають седловой траєкторією.
приклад
Знайдемо стаціонарну точку, якщо і (С) = 1,25С0*8; р = 0,1; у = 4 до. Із системи (2.21) слід: 1/24к = 0,1; до * = 25; з * => / 25 = 5. Тобто стаціонарна точка -? (25, 5).
Окремий випадок. Виробнича функція лінійна: / (К) = Ак. Тоді з (2.19) випливає, що споживання змінюється постійним темпом з = (Л |}) / 0. Воно росте при високій продуктивності технології (Л > Р) і знижується при низькій продуктивності (Л < Р), при цьому динаміка споживання не залежить від поточних значень фондоозброєності. Стаціонарної точки не існує. Рівняння (2.20) для до набуде вигляду:

Візьмемо його рішення до = до0е (А і підставимо в (2.22), отримаємо обмеження на початкові обсяги споживання і фондоозброєності:
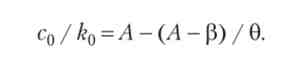
Якщо ця умова виконується, то обидва показники змінюються рівним темпом, а фазова траєкторія є прямою, що проходить через початок координат під кутом, який залежить від всіх екзогенних параметрів системи.