7.2. Використання способів парної кореляції для вивчення стохастичних залежностей
Одним з основних завдань кореляційного аналізу є визначення впливу факторів на величину результативного показника (в абсолютному вимірі). Для вирішення цього завдання підбирається відповідний тип математичного рівняння, яке найкращим чином відображає характер досліджуваної зв'язку (прямолінійною, криволінійної і т.д.). Це відіграє важливу роль в кореляційному аналізі, тому що від правильного вибору рівняння регресії залежить хід розв'язання задачі та результати розрахунків.
Обгрунтування рівняння зв'язку робиться за допомогою зіставлення паралельних рядів, угруповання даних і лінійних графіків. Розміщення точок на графіку покаже, яка залежність утворилася між досліджуваними показниками: прямолінійна або криволінійна.
Найбільш простим рівнянням, яке характеризує прямолінійну залежність між двома показниками, є рівняння прямої:
Yх=a + bx, (7.1)
де х - факторний показник; Y - результативний показник;
а і b - параметри рівняння регресії, які потрібно відшукати.
Це рівняння описує такий зв'язок між двома ознаками, при якій із зміною факторного показника на певну величину спостерігається рівномірне зростання або спадання значень результативного показника. Як приклад для ілюстрації кореляційного аналізу прямолінійною залежності можуть бути використані відомості про зміну врожайності зернових культур (Y) залежно від якості орної землі (х) (див. табл. 4.7).
Значення коефіцієнтів а і b знаходять із системи рівнянь, отриманих за способом найменших квадратів. У даному випадку система рівнянь має наступний вигляд:
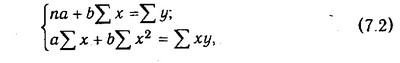
де п - кількість спостережень (у нашому прикладі - 20).
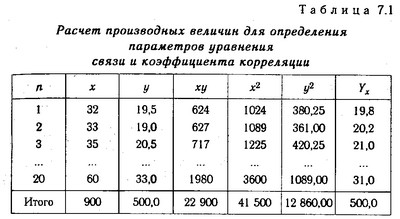
Значення розраховуються на основі фактичних вихідних даних (табл. 7.1).
Розрахунок виробничих величин для визначення параметрів рівняння зв'язку та коефіцієнта кореляції
Підставивши отримані значення в систему рівнянь, отримаємо
[20а + 900b=500;
[900А +41500 b=22 900.
Помноживши всі члени першого рівняння на 45 (900/20), отримаємо таку систему рівнянь:
[900a + 40 500b=22 500;
[9000 +41 500b=22900.
Віднімемо від другого рівняння перше. Звідси 1000b=400; b=0,4,
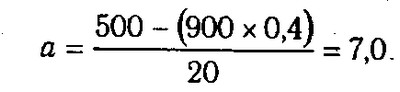
Таким чином, рівняння зв'язку, яке описує залежність врожайності від якості грунту, буде мати вигляд:
Yx=7 , 0 + 0,4 x.
Коефіцієнт а - постійна величина результативного показника, яка не пов'язана із зміною даного чинника. Параметр b показує середня зміна результативного показника з підвищенням або пониженням величини фактора на одиницю його виміру. У даному прикладі з збільшенням якості грунту на один бал врожайність зернових культур підвищується в середньому на 0,4 ц / га.
Підставивши в рівняння регресії відповідні значення х, можна визначити вирівняні (теоретичні) значення результативного показника (Y) для кожного господарства.
Yx=7 +0, 4х32=19,8 ц / га.
Отримана величина показує, якою була б врожайність при якості грунту 32 бали, якби дане господарство використовувало свої виробничі можливості в такій мірі, як у середньому всі господарства району. Аналогічні розрахунки зроблені для кожного господарства. Дані наведені в останній графі табл. 7.1. Порівняння фактичного рівня врожайності з розрахунковим дозволяє оцінити результати роботи окремих підприємств.
За таким же принципом вирішується рівняння зв'язку при криволінійній залежності між досліджуваними явищами. Якщо при збільшенні одного показника значення іншого зростають до певного рівня, а потім починають знижуватися (наприклад, залежність продуктивності праці робітників від їх віку), то для запису такої залежності найкраще підходить парабола другого порядку:
Yx=a + bx + cx2. (7.3)
Відповідно до вимог методу найменших квадратів для визначення параметрів а, b і с необхідно вирішити наступну систему рівнянь:
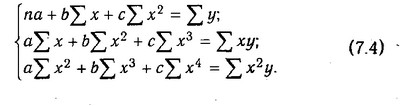
Значення знаходять на підставі вихідних даних (табл . 7.2).
Залежність продуктивності праці від віку працівників
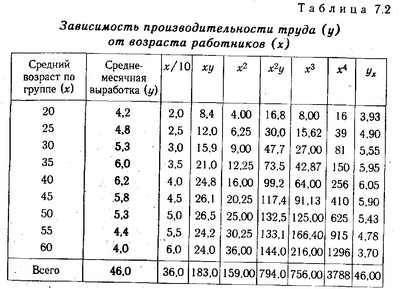
Підставивши отримані значення в систему рівнянь, отримаємо
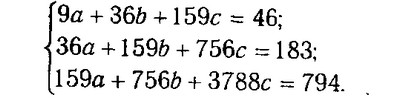
Параметри а, b і з знаходять способом визначників або способом виключення. Використовуємо спосіб визначників. Спочатку знайдемо спільну визначник:
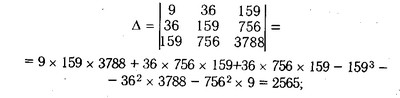
потім приватні визначники а, b і с:

Рівняння параболи буде мати наступний вигляд:
Yx=-2,67 + 4,424 x - 0,56 lx2.
Параметри отриманого рівняння економічного сенсу не мають. Якщо підставити в дане рівняння відповідні значення х, то отримаємо вирівняні значення продуктивності праці залежно від віку робітників. Результати наведені в останній графі табл. 7.2.
З таблиці видно, що продуктивність праці робітників підвищується до 40-річного віку, після чого починає знижуватися. Значить, ті підприємства, які мають більше працівників 30 - 40-річного віку, матимуть і більш високі показники продуктивності праці при інших рівних умовах. Цей фактор необхідно враховувати при плануванні рівня продуктивності праці і при підрахунку резервів її зростання.
Досить часто в економічному аналізі для запису криволінійних залежностей використовується гіпербола:
Для визначення її параметрів необхідно вирішити наступну систему рівнянь:
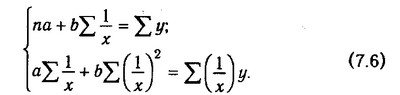
Гіпербола описує таку залежність між двома показниками, коли при збільшенні однієї змінної значення іншої збільшуються до певного рівня, а потім приріст знижується, наприклад, залежність врожайності від кількості внесеного добрива, продуктивності тварин від рівня їх годівлі, собівартості продукції від обсягу виробництва і т.
При більш складному характері залежності між досліджуваними явищами використовуються більш складні параболи (третього, четвертого порядку і т.д.), а також квадратические, статечні, показові та інші функції.
Таким чином, використовуючи той чи інший тип математичного рівняння, можна визначити ступінь залежності між досліджуваними явищами, тобто дізнатися, на скільки одиниць в абсолютному вимірі змінюється величина результативного показника із зміною факторного на одиницю. Однак регресійний аналіз не дає відповіді на питання: тісний це зв'язок чи ні, вирішальний вплив надає даний фактор на величину результативного показника або другорядне?
Для вимірювання тісноти зв'язку між факторними і результативними показниками визначається коефіцієнт кореляції.
У разі прямолінійної форми зв'язку між досліджуваними показниками коефіцієнт кореляції розраховується за такою формулою:
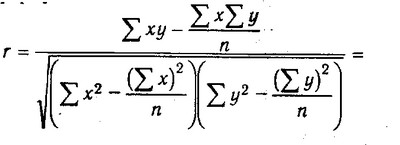
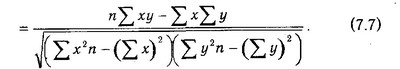
Підставляючи значення у формулу (7.7), отримуємо
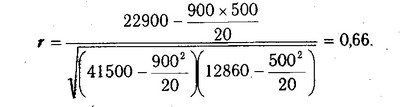
Коефіцієнт кореляції може приймати значення від О до ± 1. Чим ближче його величина до 1, тим тісніший зв'язок між явищами, що вивчаються, і навпаки. У даному випадку величина коефіцієнта кореляції є суттєвою (r=0,66). Це дозволяє зробити висновок про те, що родючість грунту - один з основних факторів, від якого в цьому районі залежить рівень врожайності зернових культур.
Якщо коефіцієнт кореляції звести в квадрат, отримаємо коефіцієнт детермінації (d=0,435). Він показує, що врожайність зернових культур на 43,5% залежить від якості грунту, а на частку інших факторів припадає 56,5% приросту врожайності.
Що стосується вимірювання тісноти зв'язку при криволінійній формі залежності, то тут використовується не лінійний коефіцієнт кореляції, а кореляційне відношення:
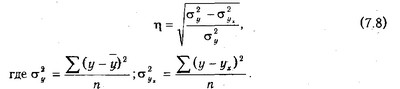
Показник (7.8) є універсальним. Його можна застосовувати при будь-якій формі залежності. Проте для визначення його величини спочатку необхідно вирішити рівняння регресії і розрахувати вирівняні значення результативного показника (Ух), для чого в отримане рівняння потрібно підставити значення х і х2 по кожній віковій групі (табл. 7.3).
Розрахунок вихідних даних для визначення кореляційного відношення при криволінійних залежностях
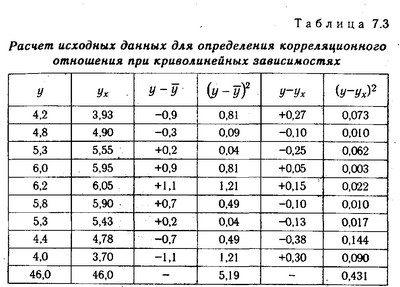
Підставивши отримані значення в формулу (7.8), визначимо величину кореляційного відносини:
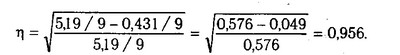
На закінчення необхідно відзначити, що ми розглянули використання способів парної кореляції тільки на двох прикладах. Однак ця методика може бути використана для дослідження співвідношень між різними економічними показниками, що дозволяє значно поглибити знання про досліджуваних явищах, визначити місце і роль кожного фактора у зміні рівня досліджуваного показника.
Інформація, релевантна " 7.2. Використання способів парної кореляції для вивчення стохастичних залежностей "
- 7.1. Поняття стохастичною зв'язку і завдання кореляційного аналізу
способи економічного аналізу, з якими ми вже знайомилися в попередніх розділах: порівняння паралельних і динамічних рядів, аналітичні угруповання, графіки. Однак вони дозволяють виявити тільки загальний характер і напрям зв'язку. Основне ж завдання факторного аналізу - визначити ступінь впливу кожного фактора на рівень результативного показника. Для цієї мети застосовуються способи - 2.8.1. Кореляційний аналіз
використанню. - 1.3. Предмет і основні методи аналізу господарської діяльності бюджетних організацій
стохастичні. Характерною особливістю детермінованих (функціональних) зв'язків є те, що зміни фактора на одиницю свого значення завжди відповідає зміна результативного показника на строго певну величину. Виділяють наступні види таких причинно-наслідкових залежностей: - аддитивная залежність - результативний показник (РП) дорівнює сумі або різниці факторів - Аналізуючи графік, ми відзначаємо, що точки, рас-покладені на площині правіше, як правило , розміщуються вище, з чого
здібності, увага з боку викладача і сніданок. Однак на рис. 2н.2 дія всіх цих факторів не враховується. З іншого боку, економістів нерідко цікавить іменнозавісімость між двома - 7.5. % R Ларрі Вільямса
використання даного індикатора на власній практиці. Строго кажучи, його розрахунок являє собою змінену формулу для% К. Вільяма рекомендує використання 10-денного періоду для розрахунків. Він має в своєму розпорядженні межі зон перекупленності і перепроданості на рівнях 90% і 10% відповідно. Правила використання лінії% R практично не відрізняються від вже викладених у відношенні стохастичних - 2.2.2. Види зв'язків в економічних системах
для кожного конкретного значення ознаки х значення у утворюють розподіл, зване умовним. Тому зміна величини х призводить до зміни величини у лише в середньому. Система називається ймовірнісної, якщо при одних і тих же початкових умов вона може переходити в різні стани, що мають різні ймовірності. Аналіз стохастичних зв'язків в імовірнісних системах буде розглянуто в - 2.8. Математико-статистичні методи вивчення зв'язків
використання їх в техніці, має певні труднощі, пов'язані з отриманням сукупності достатнього обсягу. У техніці експеримент можна повторити, в економіці цього зробити не можна. Це призводить до дискусії про правомірність використання статистичних методів при побудові факторних моделей в аналізі діяльності підприємств, оскільки при цьому нерідко доводиться працювати в умовах малих - 7.4. Стохастичні лінії (Stochastics)
використання залишається тією ж. Така заміна днів у формулі подібна використанню ковзають середніх різних порядків. 116 Рис. 7.6. Стохастичні лінії на золоті. Сигнали подаються при досягненні зон перекупленності і перепроданості, в даному випадку - 80 і 20. Графік наданий агентством Reuter 117 Одну з стохастичних ліній позначають суцільною, а іншу - пунктирною - 5.1. Поняття, типи та завдання факторного аналізу
використання для управління економічними процесами). Відбір факторів для аналізу того чи іншого показника здійснюється на основі теоретичних і практичних знань, набутих у цій галузі. При цьому зазвичай виходять з принципу: чим більший комплекс факторів досліджується, тим точніше будуть результати аналізу. Разом з тим необхідно мати на увазі, що якщо цей комплекс факторів - 2.8.2. Регресійний аналіз
використання методів кореляційного і регресійного аналізу на прикладі 2.13. Приклад 2.13. Найбільшим попитом у торговельних точках міста, які реалізовують молочну продукцію, користується молоко "Літо", що випускається в пакетах об'ємом 1 літр. Ціни за одиницю цього товару в різних торгових точках міста варіюють. Відомо, що реалізація цього продукту вносить істотний внесок у загальну виручку торгових - Висновок
використанням програми MarketWarrior. Інформацію про цю програму можна знайти на сайті - 5.3. Систематизація факторів в аналізі господарської діяльності
способи систематизації факторів у детермінованому і стохастичному аналізі. Системний підхід в АХД викликає необхідність взаємопов'язаного вивчення факторів з урахуванням їх внутрішніх і зовнішніх зв'язків, взаємодії і співпідпорядкованості, що досягається за допомогою систематизації. Систематизація в цілому - це розміщення досліджуваних явищ або об'єктів у певному порядку з виявленням їх взаємозв'язку - Г. В. Савицька. Аналіз господарської діяльності підприємства. 4-е видання, перероблене і доповнене, 2001
- 7.3. Методика множинного кореляційного аналізу
використана статечна функція: статечна функція {foto132} або логарифмічна: логарифмічна функція {foto133} Наведені моделі вигідні тим, що їх параметрами (bi) можна дати економічне пояснення (інтерпретацію). У лінійній моделі коефіцієнти bi показують, на скільки одиниць змінюється результативний показник за зміною факторного на одиницю в абсолютному вираженні, в - Кращий спосіб розібратися в ній - вивчення істо- рії розвитку економічної думки.
використанні в аналізі американської економіки. Історія кривої Філліпса Крива Філіпса - крива, що демонструє-ющая зворотну залежність між інфляцією і безра-ботіцей в коротко-терміновому пепіоде. У 1958 р. економіст А. У. Філліпс опублікував в англійському журналі «Eco-nomical статтю« Залежність між безробіттям і темпом зміни номінальною заробітної плати в - 1. Предмет і завдання курсу.
використання потенціалів національної економіки та функціонування господарських комплексів у ринковому середовищі. Фактично «Національна економіка» - той предмет, в рамках якого відбувається зіставлення теоретичних уявлень про оптимальні шляхи розвитку економіки країни з реальними економічними процесами, що не тільки дає знання про стан економіки, але і дозволяє виробляти - 27. ОСНОВНІ ПОНЯТТЯ АНАЛІЗУ ВИКОРИСТАННЯ ТРУДОВИХ РЕСУРСІВ ПІДПРИЄМСТВА
використання, високий рівень продуктивності праці мають велике значення для збільшення обсягів продукції і підвищення ефективності виробництва. Зокрема, від забезпеченості підприємства трудовими ресурсами та ефективності їх використання залежать обсяг і своєчасність виконання всіх робіт, ефективність використання устаткування, машин, механізмів, обсяг виробництва продукції, її - Д. Часто ці економічні змінні взаємозалежні. Коли зростає ціна на банани, потреби- тели обмежують їх покупки.
використанням графіків, а також деякі пастки, які виникають при використанні графічних методів. Графіки однієї змінної Три загальних графіка представлені на рис. 2п.1. Кругова діаграма (а) показує розподіл витрат на медичне обслуговування населення страхових компаній та уряду. Кожна частина кругової діаграми представляє частку кожної групи в загальному обсязі