2.8.2. Регресійний аналіз
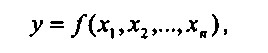
де у - залежна змінна (вона завжди одна);
хi - незалежні змінні (фактори) (їх може бути декілька).
Якщо незалежна змінна одна - це простий регресійний аналіз. Якщо ж їх декілька (п 2), то такий аналіз називається багатофакторним.
У ході регресійного аналізу вирішуються дві основні задачі:
- побудова рівняння регресії, тобто знаходження виду залежності між результатними показником і незалежними факторами x1, x2, ..., xn.
- оцінка значимості отриманого рівняння, тобто визначення того, наскільки вибрані факторні ознаки пояснюють варіацію ознаки у.
Застосовується регресійний аналіз головним чином для планування, а також для розробки нормативної бази.
На відміну від кореляційного аналізу, який тільки відповідає на питання, чи існує зв'язок між аналізованими ознаками, регресійний аналіз дає і її формалізоване вираження. Крім того, якщо кореляційний аналіз вивчає будь-яку взаємозв'язок факторів, то регресійний - односторонню залежність, тобто зв'язок, що показує, яким чином зміна факторних ознак впливає на ознака результативний.
Регресійний аналіз - один з найбільш розроблених методів математичної статистики. Строго кажучи, для реалізації регресійного аналізу необхідно виконання ряду спеціальних вимог (зокрема, xl, x2, ..., xn; y повинні бути незалежними, нормально розподіленими випадковими величинами з постійними дисперсіями). У реальному житті суворе відповідність вимогам регресійного і кореляційного аналізу зустрічається дуже рідко, проте обидва ці методу досить поширені в економічних дослідженнях. Залежності в економіці можуть бути не тільки прямими, але і зворотними і нелінійними. Регресійна модель може бути побудована за наявності будь-якої залежності, проте в багатофакторному аналізі використовують тільки лінійні моделі виду:
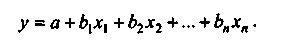
Побудова рівняння регресії здійснюється, як правило, методом найменших квадратів, суть якого полягає в мінімізації суми квадратів відхилень фактичних значень результатного ознаки від його розрахункових значень, тобто:
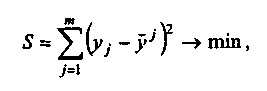
де т - число спостережень;
j=a + b1x1j + b2x2j + ... + Bnхnj - розрахункове значення результатного фактора.
Коефіцієнти регресії рекомендується визначати за допомогою аналітичних пакетів для персонального комп'ютера або спеціального фінансового калькулятора. У найбільш простому випадку коефіцієнти регресії однофакторного лінійного рівняння регресії виду y=а + b х можна знайти за формулами:
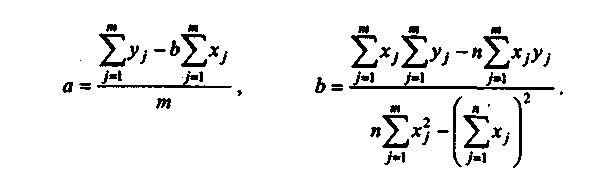
Розглянемо використання методів кореляційного і регресійного аналізу на прикладі 2.
Приклад 2.13. Найбільшим попитом у торговельних точках міста, які реалізовують молочну продукцію, користується молоко "Літо", що випускається в пакетах об'ємом 1 літр. Ціни за одиницю цього товару в різних торгових точках міста варіюють.
Відомо, що реалізація цього продукту вносить істотний внесок у загальну виручку торгових точок. Можливо, вона впливає і на величину прибутку підприємств торгівлі. Чи так це - дозволить встановити аналіз.
1. За даними, що стосуються цін на упаковку молока "Літо" та обсягів реалізації в 15 торгових точках міста, побудуємо рівняння регресійної залежності між цими факторами.
2. Методом регресійного аналізу визначимо, чи є зв'язок між величиною чистого прибутку підприємств торгівлі та обсягами реалізації ними молока "Літо", якщо для всіх 15 аналізованих точок відомі величини прибутку за II квартал 1999 р., а також ціни і обсяги реалізації даної марки молока (табл . 2.5).
Таблиця 2.Показателі діяльності торговельних підприємств, що реалізують молоко "Літо", за II квартал 1999
Показники діяльності торговельних підприємств, що реалізують молоко "Літо", за II квартал 1999
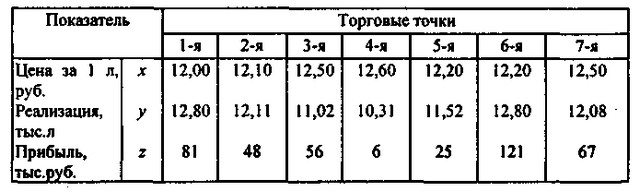
Показники діяльності торговельних підприємств, що реалізують молоко "Літо", за II квартал 1999 р. Продовження
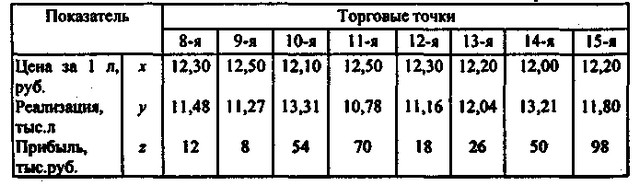
Аналіз будемо проводити за допомогою табличного процесора MS Excel . Описова статистика для представлених даних відображена в табл. 2.6.
Таблиця 2.Опісательная статистика реалізації молока "Літо" торговими точками
Описова статистика реалізації молока "Літо" торговими точками
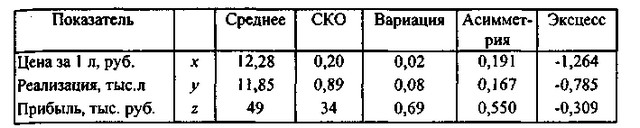
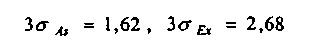
1. Аналіз варто почати з перевірки однорідності сукупності даних. Критерієм однорідності є умова:
Var <0,33.
Бачимо, що ця умова виконується лише для рядів даних, що відносяться до цін (фактор x) і обсягами реалізації (фактор у) молока.
Перевірка нормальності розподілів цих факторів показує:
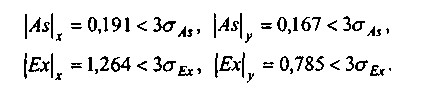
Умови нормальності виконуються, отже, за двома цими рядам даних можна будувати регресійну залежність.
Наступним кроком при побудові регресійної моделі буде визначення результативного і факторного ознак. Виходячи з суті поставленого завдання, можна сказати, що в даному випадку незалежним фактором є ціна за літр, об'єм реалізації - ознака залежний (результатний).
Регресійна залежність між факторами х і у (залежність обсягу реалізації молока від його ціни) буде мати вигляд:
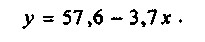
Отриманий результат - обернено пропорційна залежність між факторами - цілком узгоджується зі здоровим глуздом: очевидно, що чим вища ціна, тим менш приваблива торгова точка для покупців даного товару.
Регресійна залежність дозволяє будувати прогноз величини результативного фактора при відомій величині залежного (т.
Підставивши, наприклад, х=12,40 руб. за літр в аналітичну формулу залежності, отримаємо очікуване значення обсягу реалізації за квартал - y=11,72 тис. літрів.
2. Визначити, чи пов'язаний обсяг прибутку, отриманого підприємствами торгівлі, з обсягами реалізації ними одного виду продукції, можна за допомогою кореляційного аналізу. Матриця кореляцій, розрахована за допомогою комп'ютера, виглядає так:

Величини коефіцієнтів парної кореляції факторів такі:
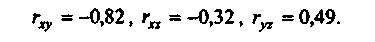
Ці величини свідчать про те, що між ціною товару (х) і обсягом його реалізації (у) зв'язок вельми тісний (величина 0,82 говорить про те, що 82% варіації фактора у пояснюються варіацією фактора х). Прибуток підприємства від ціни на цей товар залежить слабо (коефіцієнт кореляції дорівнює -0,32), а от зв'язок величини прибутку та обсягів реалізації молока "Літо" виявилася середньої сили (ryz=0,49), причому залежність прямо пропорційна.
Отже, збільшення обсягів реалізації цього товару в середньому досить помітно впливає на зростання прибутку підприємств торгівлі. За результатами аналізу керівництву магазинів слід подумати про заходи щодо стимулювання продажу молока цієї марки.
Чи можна побудувати і регресійну залежність прибутку від досліджуваних факторів?
Для повного ряду з 15 значень критерій однорідності (VаR <0,33) не виконується, отже, використовувати повний ряд значень прибутку не можна. Лише виключивши по чотири найбільших і найменших значення, можна привести цей ряд до однорідності. Перевірка нормальності для усіченої сукупності даних (по 7 залишилися магазинам) показує, що всі три ряди значень нормальні. Правда, при цьому викликає сумнів правомочність використання статистичних процедур на настільки малій вибірці. Однак якщо абстрагуватися від цього факту, то і в цьому випадку залежність виду z=а + b1х + b2у не дасть аналітику значимої інформації, оскільки між факторами х і у спостерігається сильна взаємозалежність (мультиколінеарності) - про це свідчить високе значення парного коефіцієнта кореляції (на усіченої вибірці rxy=-0,88).
Тому при регресійному аналізі прибутку доцільно брати лише один з цих факторів, а саме обсяг реалізації, оскільки його зв'язок з величиною прибутку більш тісна (ryz=0,78, тоді як rxz=0,48 - також за усіченою вибірці).
Необхідно відзначити, що в економічних дослідженнях кореляційний і регресійний аналізи нерідко об'єднуються в один - кореляційно-регресійний аналіз. Мається на увазі, що в результаті такого аналізу буде побудована регресійна залежність (тобто проведений регресійний аналіз) і розраховано коефіцієнти її тісноти й значимості (тобто проведений кореляційний аналіз). У відомому сенсі кореляційний зв'язок носить більш загальний характер, оскільки вона не передбачає наявності залежності "причина - наслідок".
Інформація, релевантна " 2.8.2. Регресійний аналіз "
- 2.8.3. Кластерний аналіз
регресійного аналізу, процедура кластеризації досить трудомістка, її доцільно виконувати на - 14. МЕТОДИ РОЗРАХУНКУ ЦІН
регресійного аналізу; 3) баловий метод; 4) агрегатний метод. Вибравши один з методів ціноутворення, необхідно прийняти саме цінове рішення, визначити конкретну ціну. Тут враховується цілий ряд аспектів, таких як психологічний вплив, вплив різних елементів маркетингу, дотримання базових цілей цінової політики, аналіз можливої реакції на прийняту - § 1. ПРЕДМЕТ І ЗАВДАННЯ СТАТИСТИКИ ФІНАНСІВ ПІДПРИЄМСТВ (ОРГАНІЗАЦІЙ)
регресійного і кореляційного аналізу, рядів динаміки, індексний метод і - Питання 65. Предмет і завдання статистики фінансів підприємств (організацій)
регресійного і кореляційного аналізу; 3) метод рядів динаміки; 4) індексний метод і - Висновок
регресійних лініях тренда. Вивчаючи методи ліній тренда більше десяти років, я переконаний, що методи ліній тренда по Ендрюсу - краще, що Ви коли-небудь могли бачити. Кореляції з ринком, які можуть бути знайдені, використовуючи інші методи ліній тренда, дуже нестійкі. Інші методи ліній тренда корелюють з ринком досить, щоб вразити ваша уява, але не достатньо, щоб робити - В.В. Ковальов, О.Н. Волкова. Аналіз господарської діяльності підприємства, 2002
- Аналіз
аналіз і синтез. При аналізі відбувається уявне розкладання явища на складові частини і виділення окремих його сторін з метою виявити те специфічне, що відрізняє їх один від одного. Це важливо для вирішення подальшої завдання теоретичного пояснення тих особливостей, від яких відволікаються спочатку. За допомогою аналізу розкривається істотне в явищі. Якщо говорити про процес - 2.2.3. Типи економічних моделей
регресивні моделі - див розділи 2.6.2 і 2.8.2), моделі ситуаційного аналізу (див. розділ 2.5.8). У зазначених розділах нашого посібника будуть розглянуті деякі теоретичні та практичні аспекти застосування подібних моделей. Нормативні моделі. Моделі цього типу дозволяють порівняти фактичні результати діяльності підприємств з очікуваними, розрахованими за бюджетом. Ці моделі використовуються - Література
аналіз в бюджетних установах. М., 1974. 4. Корчагіна Л. М. Аналіз господарської діяльності підприємства / / Бухгалтерський облік. 1996. № 10. 5. Мезенцева Т. Бухгалтерський облік і економічний аналіз в умовах ринку / / Фінанси, облік, аудит. 1994. № 6. 6. Савицька Г.В. Аналіз господарської діяльності підприємства. Мн., 1999. 7. Самбірський В.І., Грищенко А.А. Аналіз господарської - 4. Техніка та принципи проектного аналізу. Вартість грошей у часі
аналіз здійснюється на базі прийомів, які не є привілеєм проектного аналізу, а використовуються також в інших галузях теоретичної та прикладної економіки. Розглянемо деякі з цих - 13.1. АРМ менеджера як компонент інформаційно-обчислювального середовища
регресійний аналіз і ряд інших методів, одно використовуваних як для аналізу, так і для синтезу. Причому залежно від того, що є залежною змінною, а що незалежними, процес дослідження об'єднує або роз'єднує елементи, складові явище, тобто здійснюється синтез або аналіз. Економіст-аналітик «крутить» аналітичну модель багаторазово, тому немає сенсу говорити, що на