7.3. Методика множинного кореляційного аналізу
Економічні явища і процеси господарської діяльності підприємств залежать від великої кількості факторів. Як правило, кожен фактор окремо не визначає досліджуване явище у всій повноті. Тільки комплекс чинників у їх взаємозв'язку може дати більш-менш повне уявлення про характер досліджуваного явища.
Багатофакторний кореляційний аналіз складається з декількох етапів.
На першому, етапі визначаються чинники, які мають вплив на досліджуваний показник, і відбираються найбільш істотні для кореляційного аналізу.
На другому етапі збирається і оцінюється вихідна інформація, необхідна для кореляційного аналізу.
На третьому етапі вивчається характер і моделюється зв'язок між факторами і результативним показником, тобто підбирається і обгрунтовується математичне рівняння, яке найбільш точно виражає сутність досліджуваної залежності.
На четвертому етапі проводиться розрахунок основних показників зв'язку кореляційного аналізу.
На п'ятому етапі дається статистична оцінка результатів кореляційного аналізу та практичне їх застосування.
Відбір факторів для кореляційного аналізу є дуже важливим моментом в економічному аналізі. Від того, наскільки правильно він зроблений, залежить точність висновків за підсумками аналізу. Головна роль при відборі факторів належить теорії, а також практичного досвіду аналізу. При цьому необхідно дотримуватися наступних правил.
1. При відборі факторів у першу чергу слід враховувати причинно-наслідкові зв'язки між показниками, так як тільки вони розкривають сутність досліджуваних явищ. Аналіз же таких факторів, які знаходяться тільки в математичних співвідношеннях з результативним показником, не має практичного сенсу.
2. При створенні багатофакторної кореляційної моделі необхідно відбирати найбільш значущі фактори, які мають вирішальний вплив на результативний показник, так як охопити всі умови і обставини практично неможливо. Фактори, які мають критерій надійності за Стьюдентом менше табличного, не рекомендується приймати в розрахунок.
3. Всі фактори повинні бути кількісно вимірні, тобто мати одиницю виміру, і інформація про них повинна міститися в обліку та звітності.
4. У кореляційну модель лінійного типу не рекомендується включати фактори, зв'язок яких з результативним показником має криволінійний характер.
5. Не рекомендується включати до кореляційну модель взаємопов'язані чинники. Якщо парний коефіцієнт кореляції між двома факторами більше 0,85, то за правилами кореляційного аналізу один з них необхідно виключити, інакше це призведе до спотворення результатів аналізу.
6. Небажано включати в кореляційну модель фактори, зв'язок яких з результативним показником носить функціональний характер.
Велику допомогу при відборі факторів для кореляційної. моделі надають аналітичні угруповання, спосіб зіставлення паралельних і динамічних рядів, лінійні графіки. Завдяки їм можна визначити наявність, напрямок і форму залежності між досліджуваними показниками. Відбір факторів можна проводити також в процесі виконання завдання кореляційного аналізу на основі оцінки їх значимості за критерієм Стьюдента, про яке буде сказано нижче.
Виходячи з перерахованих вище вимог і використовуючи названі способи відбору факторів, для багатофакторної кореляційної моделі рівня рентабельності (Y) підібрані. наступні фактори, які чинять найбільш істотний вплив на її рівень:
x1 - матеріаловіддача, руб.;
x2 - фондовіддача, коп.;
x3 - продуктивність праці (середньорічна вироблення продукції на одного працівника), млн руб.;
x4 - тривалість обороту оборотних коштів підприємства, дні;
x5 - питома вага продукції вищої категорії якості,%.
Оскільки кореляційний зв'язок з достатньою виразністю і повнотою проявляється тільки в масі спостережень, обсяг вибірки даних повинен бути достатньо великим, так як тільки в масі спостережень згладжується вплив інших факторів. Чим більша сукупність об'єктів досліджується, тим точніше результати аналізу.
Враховуючи цю вимогу, вплив перерахованих факторів на рівень рентабельності досліджується на прикладі 40 підприємств.
Наступним етапом аналізу є збір і статистична оцінка вихідної інформації, яка використовуватиметься в кореляційному аналізі. Зібрана вихідна інформація повинна бути перевірена на достовірність, однорідність і відповідність закону нормального розподілу.
У першу чергу необхідно переконатися в достовірності інформації, наскільки вона відповідає об'єктивній дійсності. Використання недостовірної, неточної інформації призведе до неправильних результатів аналізу та висновків.
Одна з умов кореляційного аналізу - однорідність досліджуваної інформації щодо розподілу її біля середнього рівня. Якщо в сукупності є групи об'єктів, які значно відрізняються від середнього рівня, то це говорить про неоднорідність вихідної інформації.
Критерієм однорідності інформації служить середньоквадратичне відхилення і коефіцієнт варіації, які розраховуються по кожному факторному та результативному показником.
Середньоквадратичне відхилення показує абсолютне відхилення індивідуальних значень від середньоарифметичного. Воно визначається за формулою:
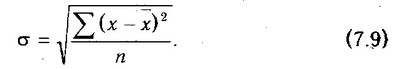
Коефіцієнт варіації характеризує відносну міру відхилення окремих значень від середньоарифметичної. Він розраховується за формулою:

Чим більше коефіцієнт варіації, тим відносно більший розкид і менша вирівняність досліджуваних об'єктів. Мінливість варіаційного ряду прийнято вважати незначною, якщо варіація не перевищує 10%, середньої - якщо становить 10-20%, значною - якщо вона більше 20%, але не перевищує 33%. Якщо ж варіація вище 33%, то це говорить про неоднорідність інформації та необхідності виключення нетипових спостережень, які зазвичай бувають в перших і останніх ранжируваних рядах вибірки.
У нашому прикладі (табл. 7.4) найвища варіація по х5 (V=22,98), але вона не перевищує 33%. Значить, вихідна інформація є однорідною і її можна використовувати для подальших розрахунків.
На підставі найвищого показника варіації можна визначити необхідний обсяг вибірки даних для кореляційного аналізу за такою формулою:
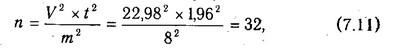
де п - необхідний обсяг вибірки даних; V - варіація,% ; t - показник надійності зв'язку, який при рівні ймовірності Р=0,05 дорівнює 1,96; т - показник точності розрахунків (для економічних розрахунків допускається помилка 5-8%).
Значить, прийнятий в розрахунок обсяг вибірки (40 підприємств) є достатнім для проведення кореляційного аналізу.
Показники статистичної характеристики вихідної інформації
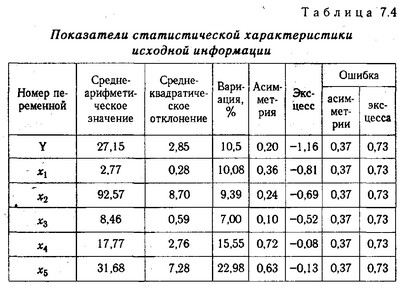
Наступна вимога до вихідної інформації - відповідність її закону нормального розподілу. Згідно з цим законом, основна маса досліджуваних відомостей по кожному показнику повинна бути згрупована близько її середнього значення, а об'єкти з дуже маленькими значеннями або з дуже великими повинні зустрічатися якомога рідше. Графік нормального розподілу інформації має наступний вигляд (рис. 7.1).
Для кількісної оцінки ступеня відхилення інформації від нормального розподілу служить відношення показника асиметрії до її помилку і відношення показника ексцесу до його помилку.
Графік нормального розподілу інформації
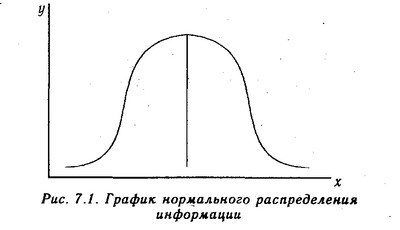
Показник асиметрії (A) і його помилка (та) розраховуються за такими формулами:
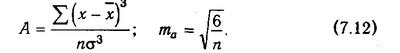
Показник ексцесу (Е) і його помилка (ті) розраховуються наступним чином:
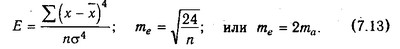
У симетричному розподілі А=0. Відмінність від нуля вказує на наявність асиметрії у розподілі даних близько середньої величини. Негативна асиметрія свідчить про те, що переважають дані з великими значеннями, а з меншими значеннями зустрічаються значно рідше. Позитивна асиметрія показує, що найчастіше зустрічаються дані з невеликими значеннями.
У нормальному розподілі показник ексцесу Е=0. Якщо Е> 0, то дані густо згруповані біля середньої, утворюючи гостровершинності. Якщо Е <О, то крива розподілу буде плосковершинной. Однак, коли відносини А / та і Е / ті менше 3, то асиметрія і ексцес не мають істотного значення і досліджувана інформація підпорядковується закону нормального розподілу.
У нашому прикладі (табл. 7.4) у всіх випадках відносини А / та і Е / ті не перевищують 3. Значить, вихідна інформація відповідає цьому закону.
Після відбору факторів і оцінки вихідної інформації важливим завданням в кореляційному аналізі є моделювання зв'язку між факторними і результативними показниками, тобто підбір відповідного рівняння, яке найкращим чином описує досліджувані залежності.
Для його обгрунтування використовуються ті ж прийоми, що і для встановлення наявності зв'язку: аналітичні угруповання, лінійні графіки та ін Якщо зв'язок всіх факторних показників з результативним носить прямолінійний характер, то для запису цих залежностей можна використовувати лінійну функцію:
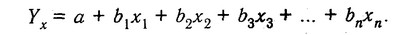
Якщо зв'язок між результативним і факторними показниками носить криволінійних характер, то може бути використана статечна функція:
ступенева функція
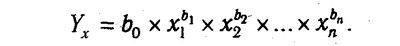
або логарифмічна:
логарифмічна функція
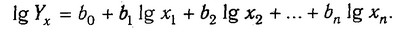
Наведені моделі вигідні тим, що їх параметрами (bi) можна дати економічне пояснення (інтерпретацію). У лінійній моделі коефіцієнти bi показують, на скільки одиниць змінюється результативний показник за зміною факторного на одиницю в абсолютному вираженні, в статечних і логарифмічних - у відсотках.
У випадках, коли важко обгрунтувати форму залежності, рішення задачі можна провести за різними моделями і порівняти отримані результати. Адекватність різних моделей фактичним залежностям перевіряється за критерієм Фішера, показником середньої помилки апроксимації і величиною множинного коефіцієнта детермінації, про які мова піде дещо пізніше (див. § 7.4).
Вивчення взаємозв'язків між досліджуваними факторами і рівнем рентабельності показало, що всі залежності в нашому прикладі мають прямолінійний характер. Тому для їх опису використана лінійна функція.
Рішення завдання багатофакторного кореляційного аналізу проводиться на ПЕОМ за типовими програмами. Спочатку формується матриця вихідних даних (табл. 7.5), у першій колонці якої записується порядковий номер спостереження, в другій - результативний показник (Y), а в наступних - факторні показники (хi).
Ці відомості вводяться в ПЕОМ і розраховуються матриці парних і приватних коефіцієнтів кореляції, рівняння множинної регресії, а також показники, за допомогою яких оцінюється надійність коефіцієнтів кореляції і рівняння зв'язку: критерій Стьюдента, критерій Фішера, середня помилка апроксимації, множинні коефіцієнти кореляції і детермінації.
Вихідні дані для кореляційного аналізу
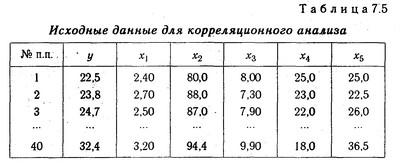
Вивчаючи матриці парних і приватних коефіцієнтів кореляції, можна зробити висновок про тісноту зв'язку між досліджуваними явищами. Коефіцієнти парної кореляції характеризують тісноту зв'язку між двома показниками в загальному вигляді з урахуванням взаємозв'язків факторів, що роблять вплив на результативний показник.
Дані табл. 7.6 (перший стовпець) свідчать про те, що всі фактори роблять відчутний вплив на рівень рентабельності. Особливо тісний зв'язок рентабельності з матеріаловіддача, фондоотдачей, якістю продукції та продуктивністю праці. Із збільшенням даних показників рівень рентабельності підвищується (прямий зв'язок). При збільшенні тривалості обороту коштів рентабельність знижується (зворотний зв'язок).
Матриця парних коефіцієнтів кореляції
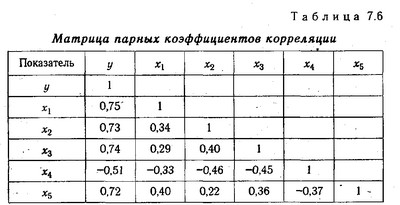
Однак необхідно відзначити, що парні коефіцієнти кореляції отримані за умови впливу інших факторів на результат. Щоб абстрагуватися від їх впливу і отримати кількісну характеристику зв'язку між результативним і факторними показниками в чистому вигляді, розраховуються приватні коефіцієнти кореляції (табл. 7.7).
При порівнянні приватних коефіцієнтів кореляції з парними видно, що вплив інших факторів на тісноту зв'язку між рівнем рентабельності і досліджуваними факторами досить значуща: приватні коефіцієнти кореляції набагато нижче парних. Це говорить про те, що фактори, які входять в дану кореляційну модель, роблять на рентабельність не тільки безпосередній вплив, а й непряме. Тому взаємозв'язку, очищені від впливу супутніх факторів, вийшли менш тісними. У деяких випадках вони можуть виявитися більш тісними, якщо виключити вплив чинників, які діють у протилежному напрямку.
Матриця приватних коефіцієнтів кореляції
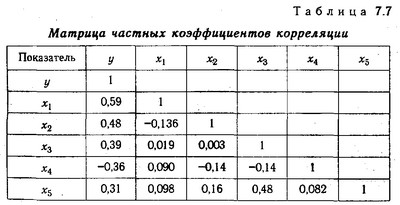
Таким чином, за допомогою парних і приватних коефіцієнтів кореляції можна отримати уявлення про тісноту зв'язку між досліджуваними явищами в загальних і безпосередніх соприкосновениях.
Значний інтерес представляють коефіцієнти кореляції, що характеризують взаємозв'язок факторів між собою. Як вже зазначалося, в кореляційну модель треба підбирати незалежні між собою фактори. Якщо коефіцієнт кореляції двох факторів вище 0,85, то один з них необхідно виключити з моделі. Дослідження матриці коефіцієнтів кореляції дозволяє зробити висновок, що в дану модель включені фактори, які не дуже тісно пов'язані між собою.
При вивченні тісноти зв'язку треба мати на увазі, що величина коефіцієнтів кореляції є випадковою, залежною від обсягу вибірки. Відомо, що зі зменшенням кількості спостережень надійність коефіцієнтів кореляції падає, і навпаки, при збільшенні кількості спостережень надійність коефіцієнтів кореляції зростає.
Значимість коефіцієнтів кореляції перевіряється за критерієм Стьюдента:
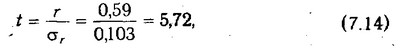
де - среднеквадратическая помилка коефіцієнта кореляції, яка визначається за формулою:
среднеквадратическая помилка коефіцієнта кореляції
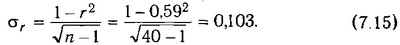
Якщо розрахункове значення (вище табличного, то можна зробити висновок про те, що величина коефіцієнта кореляції є значущою. Табличні значення t знаходять по таблиці значень критеріїв Стьюдента. При цьому враховуються кількість ступенів свободи (V=п - 1) і рівень довірчої ймовірності (в економічних розрахунках зазвичай 0,05 або 0,01). У нашому прикладі кількість ступенів свободи одно: п - 1=40 - 1=39. При рівні довірчої ймовірності Р=0,05; t=2,02. Оскільки (фактичне (табл. 7.8) у всіх випадках вище t-табличного, зв'язок між результативним і факторними показниками є надійною, а величина коефіцієнтів кореляції - значимою.
Фактичне значення критерію Стьюдента

Наступний етап кореляційного аналізу-розрахунок рівняння зв'язку (регресії). Рішення проводиться звичайно кроковим способом. Спочатку в розрахунок приймається один фактор, який надає найбільш значущий вплив на результативний показник, потім другий, третій і т.д. І на кожному кроці розраховуються рівняння зв'язку, множинний коефіцієнт кореляції і детермінації, F-відношення (критерій Фішера), стандартна помилка і інші показники, за допомогою яких оцінюється надійність рівняння зв'язку. Величина їх на кожному кроці порівнюється з попередньою. Чим вище величина коефіцієнтів множинної кореляції, детермінації і критерію Фішера і чим нижче величина стандартної помилки, тим точніше рівняння зв'язку описує залежності, що склалися між досліджуваними показниками. Якщо додавання наступних факторів не покращує оціночних показників зв'язку, то треба їх відкинути, тобто зупинитися на тому рівнянні, де ці показники найбільш оптимальні.
Порівнюючи результати на кожному кроці (табл.7.9), ми можемо зробити висновок, що найбільш повно описує залежності між досліджуваними показниками п'ятифакторна модель, отримана на п'ятому кроці. В результаті рівняння зв'язку має вигляд:
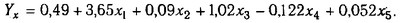
Результати розрахунку рівняння зв'язку
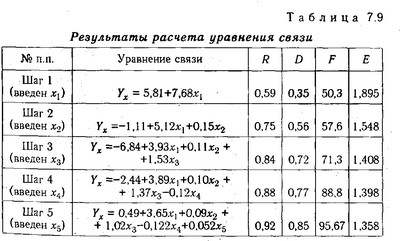
Коефіцієнти рівняння показують кількісне вплив кожного фактора на результативний показник за незмінності інших. У даному випадку можна дати наступну інтерпретацію отриманого рівняння: рентабельність підвищується на 3,65% при збільшенні материалоотдачи на 1 руб.; На 0,09% - з ростом фондовіддачі на 1 коп.; На 1,02%-з підвищенням середньорічної вироблення продукції на одного працівника на 1 млн руб.; на 0,052% - при збільшенні питомої ваги продукції вищої категорії якості на 1%. Зі збільшенням тривалості обороту коштів на 1 день рентабельність знижується в середньому на 0,122%.
Коефіцієнти регресії в рівнянні зв'язку мають різні одиниці виміру, що робить їх непорівнянними, якщо виникає питання про порівняльну силу впливу факторів на результативний показник. Щоб привести їх у порівнянний вид, всі змінні рівняння регресії виражають у частках середньоквадратичного відхилення, іншими словами, розраховують стандартизовані коефіцієнти регресії. Їх ще називають бетта-коефіцієнтами по символу, який прийнятий для їх позначення (р).
Бетта-коефіцієнти і коефіцієнти регресії пов'язані наступним відношенням:

Бетта-коефіцієнти показують, що якщо величина фактора збільшиться на одне середньоквадратичне відхилення, то відповідна залежна змінна збільшиться чи зменшиться на частку свого середньоквадратичного відхилення. Зіставлення бетта-коефіцієнтів дозволяє зробити висновок про порівняльну ступенем впливу кожного фактора на величину результативного показника. У нашому прикладі найбільший вплив на рівень рентабельності надають ма-лоотдача, фондовіддача і продуктивність праці (табл. 7.10).
За аналогією можна зіставити і коефіцієнти еластичності, які розраховуються за формулою:
коефіцієнт еластичності

Коефіцієнти еластичності показують, на скільки відсотків в середньому змінюється функція зі зміною аргументу на 1%.
коефіцієнти еластичності і бета - коефіцієнти
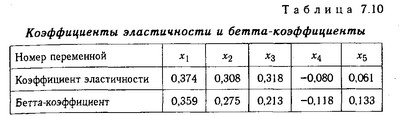
Згідно з даними табл. 7.10, рентабельність зростає на 0,374% при збільшенні рівня материалоотдачи на 1%, на 0,308% - при підвищенні фондовіддачі на 1% і т.д.
Інформація, релевантна "7.3. Методика множинного кореляційного аналізу"
- 7.1. Поняття стохастичною зв'язку і завдання кореляційного аналізу
методика вирішення завдань детермінованого факторного аналізу. Однак на практиці далеко не всі економічні явища і процеси можуть вивчатися за допомогою цієї методики, так як в більшості випадків їх не можна звести до функціональних залежностях, коли величиною факторного показника відповідає єдина величина результативного показника. Частіше в економічних дослідженнях зустрічаються - 2.8.1. Кореляційний аналіз
кореляційний зв'язок може кількома шляхами. Найважливіший з них - причинний залежність варіації результативної ознаки від зміни факторного. Крім того, такий вид зв'язку може спостерігатися між двома наслідками однієї причини. Основною особливістю кореляційного аналізу варто визнати те, що він встановлює лише факт наявності зв'язку й ступінь її тісноти, не розкриваючи її причин. У - Г. В. Савицька. Аналіз господарської діяльності підприємства. 4-е видання, перероблене і доповнене, 2001
- 5.1. Поняття, типи та завдання факторного аналізу
методика комплексного і системного вивчення і вимірювання впливу факторів на величину результативних показників. Розрізняють такі типи факторного аналізу: детермінований і стохастичний; прямий і зворотний; одноступінчатий і багатоступінчастий; статичний і динамічний; ретроспективний і перспективний (прогнозний). Детермінований факторний аналіз являє собою методику - 3.3.6. Економічний і фінансовий аналіз
методиках його - Методи історико-економічного аналізу
методики. Перевага кількісних методів - їх об'єктивність і можливість отримання принципово новою в порівнянні з іншими методами дослідження інформації; 2) методи соціологічних досліджень і соціальної психології, що мають особливе значення для аналізу історико-економічних ситуацій, оскільки народні маси роблять безпосередній вплив на хід історичних та економічних - Література
аналізу діяльності НДІ і КБ / ЦНДІ «РУМБ», 1983. 5. Самбірський В.І., Грищенко А.А. Аналіз господарської діяльності в бюджетних і наукових установах: Підручник. М., 1989. 6. Скрипченко Д.Г. Оплата праці та шляхи її реформування. Мн., 1997. 7. Довідковий посібник з аналізу діяльності наукових організацій / А.К. Казанцев, Б.І. Майданчик, Б.Д. Моторигін та ін М., 1989. 8. Скільки «мані» у - 1. Методика складання та теорії платіжного балансу
1. Методика складання та теорії платіжного - 6.1. Загальна характеристика методів фільтрації
методики є свої переваги і недоліки. У цілому ж їх правильне використання може призвести до значних прибуткам. Хоча дані методики і не так суб'єктивні, як викладені раніше фігури, все ж їх застосування вимагає деякого рівня майстерності. Вивчення основних понять і "фізичного змісту" кожної методики не займе багато часу, але може бути у вищій ступені не марно. Навіть - 4.10. Аналіз обсягу виробництва і реалізації продукції
методики аналізу базуються в основному на відкритій, тобто доступною будь-якому користувачу, бухгалтерської звітності. Тим часом в рамках внутрішнього аналізу, коли аналітик має доступ до додаткових джерел інформації, аналітичні процедури можуть бути істотно розширені. Аналіз в цьому випадку стосується головним чином ідентифікації та оцінки внутрішніх факторів зростання обсягу виробництва, а