Попит на гроші і облігації

Система домогосподарств розподіляє фіксований дохід у молодості (Y = М + В) між грошима (М) і облігаціями (В). Гроші можна використовувати в кожному періоді, вони не дають доходу. Облігації забезпечують номінальну прибутковість (г), але їх можна використовувати тільки в старості. позначимо через Р_{ і Р₂ рівні цін, З_х і З₂ - споживання в молодості і старості, М / Y - попит на гроші, або частка грошей в доході.

Є домогосподарства двох типів. Перші «живуть сьогоденням», їх частка дорівнює вони не купують облігації і витрачають всі гроші в молодості, їх споживання є функція обсягу грошей:

Якби вони ставили завдання максимізації корисності незалежно від домогосподарств другого типу, то їх споживання становило б Y / Р_х.

Домогосподарства другого типу «живуть майбутнім», їх частка дорівнює (1 - q), вони споживають тільки в старості, їх споживання одно реальної вартості грошей і облігацій з відсотками і також є функцією обсягу грошей:

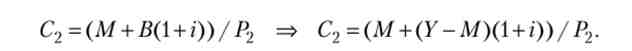
Якби вони максимізувати корисність незалежно від домогосподарств першого типу, то їх споживання було б одно (У - М) ( 1 + / ') / Р₂.

Рівновага системи домогосподарств - середньозважена величина корисності домогосподарств різного типу максимальна:

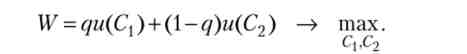
Оскільки обсяги споживання домогосподарств різного типу залежать від обсягу грошей, цільова функція суспільства є функцією однієї змінної - обсягу грошей:

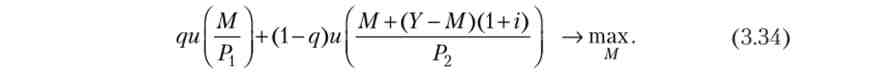
Прирівняємо нулю похідну (3.34) по М, тоді з урахуванням рівності Р₂ / Р = + до отримаємо умову рівноваги:

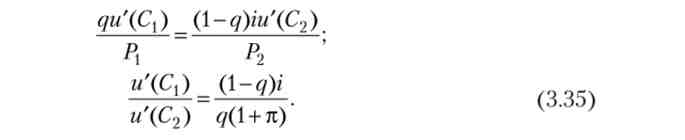
При відомої функції корисності і параметрах q і i рівність (3.35) дозволяє отримати попит на гроші як функцію темпу інфляції (л). Окремий випадок 1. і = 4 с. Тоді рівність (3.35) набуде вигляду

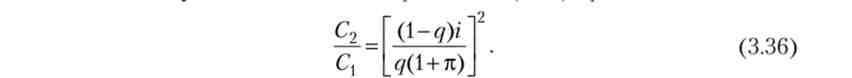
Висловимо обсяги споживання через обсяг грошей:

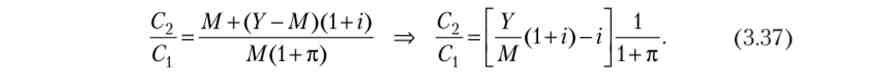
Прирівняємо праві частини (3.36) і (3.37), отримаємо функцію попиту на гроші:

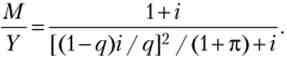
З неї випливає, що з ростом темпу інфляції попит на гроші зростає.

якщо q = 0, т. Е. Все домогосподарства «живуть майбутнім», попит на гроші дорівнює нулю і весь обсяг грошей витрачається на покупку облігацій з метою отримати максимальний відсоток і максимальне споживання в старості.

Окремий випадок 2. Функція корисності лінійна: і = С. тоді похідна W ' не залежить від обсягу грошей: якщо вона позитивна, то попит на гроші максимальний і дорівнює прибутку, якщо вона негативна, то попит на гроші дорівнює нулю. Вважаємо ставку відсотка (прибутковість облігацій) змінної, знайдемо її значення, при якому W '= 0:

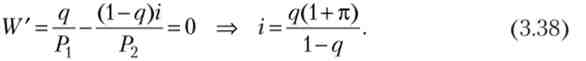
Якщо ставка більше цього значення, то W ' < 0, і попит на гроші падає до нуля, оскільки облігації більш привабливі. Якщо вона менше цього значення, то W ' > 0, і попит на гроші максимальний і дорівнює прибутку.

Припустимо, що функція корисності лінійна, а ставка відсотка підтримується на такому рівні, щоб інтегральна корисність домогосподарств не залежала від реального попиту на гроші. Тоді формула (3.38) дозволяє визначити частки домогосподарств різного виду на основі фактичних значень ставки відсотка і темпу інфляції. З рівності (3.38) слід:

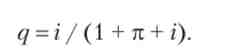
Оскільки темп інфляції зазвичай наближено дорівнює ставці відсотка, дана формула набуває вигляду: q = i / (1 + 2г). З неї при малих ставках відсотка отримуємо наближене рівність: q ~ i.

Висновок. Якщо корисність домогосподарства дорівнює його доходу, а ставка відсотка підтримується на такому рівні, що інтегральна корисність всіх домогосподарств не залежить від реального попиту на гроші, то питома вага домогосподарств, які «живуть сьогоднішнім днем» і не роблять заощаджень на старість, дорівнює ставці відсотка. Оскільки ставка відсотка в розвинених країнах зазвичай не перевищує кількох відсотків, ми приходимо до висновку, що домогосподарства даного виду становлять абсолютну меншість, а більшість домогосподарств робить заощадження на старість.

1. П'ять демографічних і кредитних хвиль стародавнього Риму
   Перший цикл - трьохсотлітній: від стабільності до нестабільності. Перший досить вивчений демографічний цикл був в Древньому Римі між 650 і 350 рр. до н.е. Максимальна чисельність населення була досягнута до 500 р. До н.е. е. Рим процвітав, набув значного поширення кредитування багатими городянами
2. Прямі інвестиції в економіці, інвестиції в основний капітал та іноземні інвестиції як базові показники в прогнозних моделях
   У ринковій економіці інвестиції представлені великим різноманіттям видів і форм і виконують різні функції. В рамках цього розмаїття інвестиції є джерелом фінансування придбання, ремонту та реконструкції основних фондів. інвестиції - грошові кошти, цінні папери, інше майно, в тому числі майнові
3. Проста екстраполяція., екстраполяція тренду
   Для стаціонарного часового ряду в якості прогнозного значення може використовуватися середнє значення рівнів ряду, т. Е. Уе = у, де уе - прогнозне значення, е - період попередження. Подібна екстраполяція дає точкову оцінку. Однак оскільки подібні прогнози грунтуються на інформації про поведінку
4. Програмно-цільовий метод. Розробка і реалізація державних програм
   Застосування методів індикативного планування тісно пов'язане з використанням державного програмування. Программноцелевой метод є одним з основних інструментів індикативного планування. Він набув широкого поширення в управлінні економічними об'єктами, процесами, відносинами на міждержавному
5. Прогнозування міжгалузевого балансу, методи прогнозування галузевих елементів кінцевого попиту
   Розробка коефіцієнтів витрат прогнозного МОБ статистичними методами передбачає побудову серії міжгалузевих таблиць за досить тривалий ретроспективний період часу. Досвід складання МОБ в різних країнах показує, що необхідна для застосування статистичних методів інформація про міжгалузевих зв'язках
6. Прогноз коефіцієнтів прямих витрат
   Основою для початкової формулювання методу «Витрати - Випуск» була гіпотеза про незмінність коефіцієнтів прямих витрат при зміні обсягів виробництва. Але з плином часу деякі коефіцієнти витрат можуть змінюватися в результаті впровадження нових методів виробництва (нових технологій). Ще В.
7. Проблема бідності
   Особливу значущість в будь-якій країні має проблема бідності. Наявність людей, що живуть за межею бідності, з доходами нижче величини прожиткового мінімуму, погіршує сприйняття економічної ситуації з боку всіх верств населення, змушує державу активізувати соціальну політику допомоги бідним.
8. Принципові особливості розробки довгострокового прогнозу
   Довготривалий розвиток характеризується принциповим наявністю вже в середньостроковому часовому горизонті ключових розвилок в політиці, що проводиться, вибір в рамках яких може зумовити кардинально різні сценарії в довгостроковій перспективі, а також наявністю ключових розвилок в розвитку