Оптимальна структура змішаного фінансового портфеля

Якщо інвестор одночасно з покупкою акцій може позичати і позичати гроші за фіксованою ставкою відсотка (г), то його портфель буде складатися з двох якісно різних частин - ризикової (П) і безризиковою (1 - п). Назвемо такий портфель змішаним. Математичне сподівання прибутковості змішаного портфеля розраховується за формулою

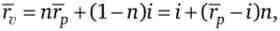
де r_v - очікувана прибутковість змішаного портфеля; г_р - очікувана прибутковість його ризикової частини, що складається з акцій.

Оскільки на грошовому ринку можна не тільки позичати, але й займати, то п може бути більшим за одиницю. Якщо, наприклад, з кожних 100 руб., Вкладених індивідом в покупку акцій, тільки 80 руб. його власні, а 20 руб. позикові, то п = 1,25.

Так як ставка відсотка однозначно визначена, то ризик змішаного портфеля дорівнює ризику міститься в ньому пакета акцій:

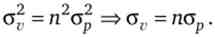
Як очевидно з наведених формул, очікувана прибутковість змішаного портфеля і її стандартне відхилення лінійно залежать від п тому між ними теж існує лінійна залежність

Отже, безліч поєднань дохідності та ризику змішаного портфеля утворює пряму лінію. Її нахил визначається відношенням (7_р - 0 / о_р, т. е. залежить того, який пакет акцій вибирає інвестор. 1 lepacno- лежання до ризику інвестор зацікавлений в тому, щоб ця пряма мала якомога більший нахил до осі абсцис (щоб при незмінному ризик збільшувалася очікувана прибутковість змішаного портфеля). У той же час область вибору змішаного портфеля повинна мати хоча б одну спільну точку з безліччю ефективних портфелів акцій. Тому при спільному існуванні ринку ризикових активів і досконалого грошового ринку, на якому можна необмежено позичати і займати, областю ефективного вибору інвестора стає пряма, яка перетинає вісь ординат в точці i і що є дотичною до кривої ефективної безлічі портфелів ризикових цінних паперів. На рис. 5.7 це пряма Ш, дотична до ефективного з ризикових портфелів Z; її рівняння

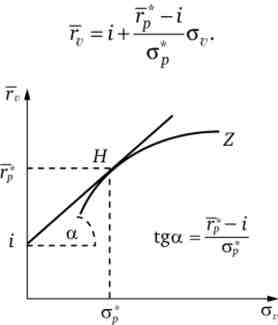
Мал. 5.7. Безліч ефективних змішаних портфелів - пряма iH

З появою досконалого ринку грошей зі всієї безлічі ефективних портфелів ризикових активів залишається тільки один, представлений точкою Я. Саме цей портфель типовий інвестор буде включати до складу майна в якості ризикової його частини. Її величина залежить від функції корисності (розташування кривих байдужості) інвестора: точка дотику прямої ефективного вибору з однією з кривих байдужості визначає оптимальну структуру його майна. На рис. 5.8 показані три можливих випадку. Вибір точки Я означає, що всі свої кошти інвестор вклав в ризикові активи. Всі точки, розташовані лівіше точки Я (наприклад, К), відповідають певному розподілу коштів між акціями і грошовою позикою. Точки, що знаходяться правіше точки Я (наприклад, L), Представляють майно, яке складається з портфеля акцій і грошової заборгованості інвестора.

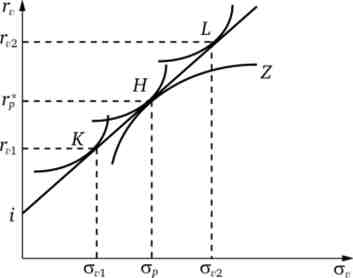
Мал. 5.8. Залежність структури змішаного портфеля від переваг інвестора 136

Таким чином, структура пакета ризикових активів, що міститься в змішаному портфелі індивіда, не залежить від його переваг щодо дохідності та ризику. Функція корисності індивіда визначає не структуру ризикового портфеля, а поведінка інвестора на грошовому ринку: чи буде він кредитором (точка До), Або позичальником (точка L), або взагалі не буде виходити на грошовий ринок (точка Н). Оптимальна структура портфеля акцій не залежить від переваг інвесторів. Цей висновок отримав назву теорема сепаратні Тобіна: Оптимізація структури портфеля ризикових цінних паперів і розподіл вкладень між ринком грошей і капіталу здійснюються окремо один від одного.

приклад 5.3

На ринку капіталу звертаються дві акції з наступними характеристиками:

Два інвестора вирішили вкласти по 1000 ден. од. кожен в ці акції. Функція корисності l-ro інвестора U_x = 5г - а², а 2-го - U₂ = 20г - а². Визначимо, скільки яких акцій купить кожен інвестор в заданих умовах і як зміниться структура їх пакетів акцій, якщо на грошовому ринку можна буде необмежено займати і позичати за ставкою i = 8,5%.

Позначимо частку акцій в портфелі п_А. тоді г_р = 25л_Л -I-15 (1 - п_л) -> п_л = ОДТу, -1,5. Тому варіацію прибутковості портфеля можна представити у вигляді функції від прибутковості:

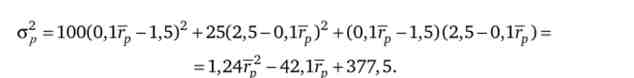
Тепер переваги 1-го інвестора можна уявити функцією від однієї змінної: [/, = 47,17 ^ - 1,247 ^²- 377,5. Вона досягає максимуму при 47,1 - 2,487 ^ = 0 -> -> г_р = 19; з_р = 5. Частка акцій А в портфелі 1-го інвестора п_Л = 0,1-19 - 1,5 = 0,4, т. Е. 400 ден. од. 1-й інвестор вкладе в акції А і 600 ден. од. в акції В.

Висловивши в функції корисності 2-го інвестора варіацію через прибутковість, отримаємо: U₂ = 62, _p- 1,247 ^²- 377,5. Вона досягає максимуму при 62,1 -2,487 ^ = 0 -> 7_р = 25; про_р = 10. Обчислимо частку акцій А в портфелі 2-го інвестора: п_А = 0,1 * 25 - 1,5 = 1; т. е. 2-й інвестор буде купувати тільки акції А.

При наявності ринку грошей областю вибору інвесторів стає лінія CML. Обидва інвестора куплять портфель акцій, відповідний точці дотику лінії CML і кривої ефективної безлічі портфелів з акцій А і В. Рівняння цієї кривийой виводиться з вирішення рівності а² = 1,247 ^ -42,17 ^, +377,5 щодо: Т_р = 17 + ^ 0,8А² -16,3. З урахуванням цього рівняння лінії CML можна записати в такий спосіб:

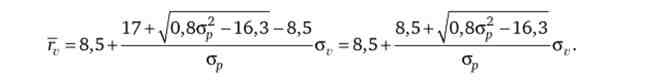
Для визначення координат точки дотику лінії CML і кривої ефективної безлічі портфелів з акцій А і В прирівняємо похідні функцій г_р(а_р) і г_г(ст_г) друг до друга:

Отже, при наявності досконалого ринку грошей обидва інвестори будуть купувати портфель акцій з очікуваною прибутковістю 19% і стандартним відхиленням 5%. Тепер рівняння лінії CML можна записати так: 7_V= 8,5 + [(19 - 8,5) / 5 a_v = 8,5 + 2,1 ст_г. Це рівність виконує роль бюджетного обмеження при максимізації функцій корисності інвесторів. Тому функцію корисності 1-го інвестора можна записати так: U_x = 5 (8,5 + 2,1ст_г) - ст_г.², а 2-го інвестора - U₂ = 20 (8,5 + 2,1о_г) - a_v². У 1-го інвестора вона досягає максимуму при ст₇, = 5, г_г = 19, а у 2-го - при ст_р = 21, 7_V = 52,6. З появою можливості займати і позичати гроші 1-й інвестор не змінив структуру своїх вкладень. Структура вкладень в ризикові і безризикові активи 2-го інвестора визначається відношенням a_v/ c_{/ t} = 21/5 = 4,2. Це означає, що 2-й інвестор вкладе в покупку оптимального портфеля акцій 1000 - 4,2 = 4200 деп. од., зайнявши 3200 ден. сд. на грошовому ринку. Після повернення позики з відсотками у нього залишиться 4200 - це 19 - 3200 - 8,5 = 52 600 ден. од., т. е. прибутковість його вкладень складе 52,6%. Наочно положення інвесторів на ринку фінансів в умовах розглянутого прикладу представлено на рис. 5.9.

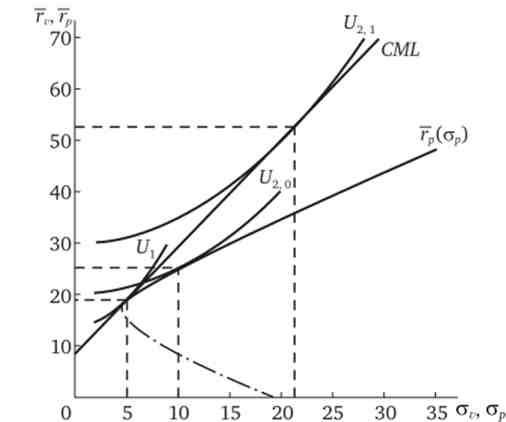
Мал. 5.9. Поведінка інвестора на ринку фінансів

1. Плаваючий обмінний курс
   Розглянемо наслідки грошово-кредитної і фіскальної політики в разі плаваючого обмінного курсу. Нехай держава вирішує стимулювати випуск за рахунок збільшення держзакупівель на величину AG. Крива IS зсувається вправо вгору. Короткострокова рівновага переміщається з точки А в точку В (рис. 16.12).
2. Планування і прогнозування як основні функції державного управління національною економікою, суть і призначення планування і прогнозування
   В результаті вивчення даного розділу студент повинен: знати основні поняття, категорії, методи і інструменти макроекономічного прогнозування; предмет і структуру макроекономічного плану і прогнозу; систему показників і основні методи планування; структуру національної економіки; вміти виявляти
3. Підстроювання цін
   Розглянемо два варіанти поведінки фірми: встановити єдину для ринку ціну або оптимальну для себе ціну з урахуванням єдиної ціни. Попит на продукт г-го виробника (Q,) пропорційний доходу (У) і скорочується зі зростанням відносної ціни (Р ; / Р ), А рівноважна реальна зарплата (W / Р) є статечна
4. Перевагу ліквідності Кейнса проти боргової дефляції Фішера
   Сенс терміна «пастка ліквідності» сьогодні повністю змінився. Кругман звільнив його від ідеї природної процентної ставки. У нових умовах центральні банки не в змозі забезпечити стан «природності» просто в силу того, що вже досягли практично нульового рівня. У ряді випадків процентна ставка
5. Передмову
   Даний підручник узагальнює досвід багаторічного викладання макроекономіки студентам різних освітніх програм на факультеті економіки Європейського університету в Санкт-Петербурзі і на кафедрі економічної кібернетики економічного факультету Санкт-Петербурзького державного університету. Різні
6. Особливості ведення бізнесу, тіньова економіка
   Інвестиційний клімат в національній економіці залежить також і від інституційних особливостей країни, від стабільності і передбачуваності відносин між владою і бізнесом, від наявності чітких, ясних і прозорих правил, що регулюють взаємодії в господарської області. В цьому плані позиції Росії
7. Основні великі монополісти міста вугільної і металургійної галузі
   Кузнецький металургійний комбінат, який протягом 70 років поставляв свою продукцію за кордон і в усі регіони СРСР, був утворений в 1932 р У період ВВВ комбінат привніс свій героїчний внесок у перемогу, випускаючи оборонну продукцію, в честь чого 9 травня 1985 був відкрито Меморіальний музей
8. Основні поняття макроекономіки, учасники макроекономічних відносин, основні поняття макроекономіки, предмет і основні проблеми макроекономіки, предмет макроекономіки
   В результаті вивчення матеріалу даного розділу студент повинен: знати поняття макроекономіки, відмінність предмета макроекономіки від предмета мікроекономіки; основні історичні етапи розвитку макроекономіки; основні макроекономічні ринки; сутність макроекономічної моделі кругообігу доходів