Оптимальний портфель ризикових цінних паперів

На безлічі ефективних портфелів кожен інвестор вибирає той, який найкращим чином відповідає його уподобанням щодо дохідності та ризику, т. Е. Максимізує свою функцію корисності U = U (r, а). Яку точку на кривій вибору віддасть перевагу інвестор, залежить від його ставлення до ризику. По відношенню до ризику людей можна розділити на три нерівні групи: люблячі ризик, байдужі до ризику і неприхильність до ризику. Більшість людей належить до третьої групи. Вони готові платити за запобігання або зниження ризику. На цьому заснована діяльність страхових компаній, що успішно функціонують в більшості країн.

Для угруповання людей по їх відношенню до ризикового доходу скористаємося поняттям «Гарантований еквівалент лотереї». Це гарантований дохід заданої величини, який має для індивіда таку ж корисність (забезпечує такий же приріст його добробуту), як і можливість брати участь в лотереї з заданою вірогідністю певного виграшу. Проілюструємо застосування цього критерію таким прикладом.

Учасникам колективного заповнення кросворду за відгадане слово пропонується на вибір або відразу отримати 5000 руб., Або вийняти наосліп з урни куля; якщо куля виявиться корисним, то гравець отримує 10 000 руб., якщо жовтим, то 8000 руб., а якщо синім, то 10 00 руб. При цьому відомо, що в урні знаходиться 2 червоних, 3 жовтих і 5 синіх куль. Ті учасники, які захочуть виймати кулю, схильні до ризику, так як гарантованого доходу в розмірі 5000 руб. вони вважають за краще ризиковий дохід з математичним очікуванням: 0,2 - 10 000 + 0,3 - 8000 + 0,5 - 1000 = 4900 руб. Коли очікуваний виграш цієї лотереї зросте до 5000 руб. (Наприклад, в результаті того, що за вийнятий червоний куля будуть платити 10 500 руб.), Тоді витягати кулі захочуть і байдужі до ризику гравці. Чи не розташовані до ризику учасники підуть до урни тільки в тому випадку, якщо очікуваний виграш перевищить 5000 руб.

Різниця між очікуваною величиною імовірнісного доходу і його гарантованим еквівалентом називають премією за ризик. Типовий інвестор не вважає ризик благом і вимагає за нього премію.

Просту функцію користі не розташованих до ризику людей запропонував М. Рубінштейн: U = щ_р-про_р, де / - коефіцієнт, що характеризує індивідуальні переваги інвестора щодо дохідності та ризику.

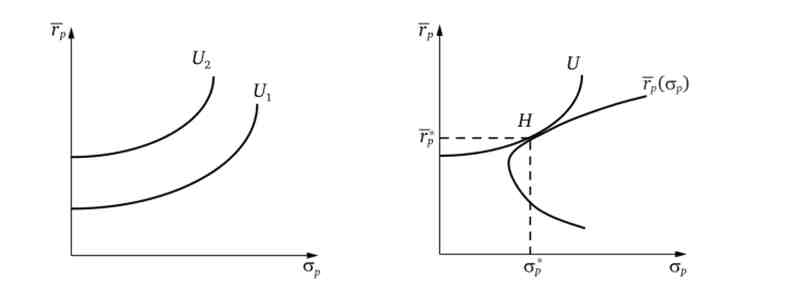
Графічно така функція зображується у вигляді сімейства кривих байдужості інвестора (рис. 5.5), побудованих але формулою r_p = (U₀ +з) / | /, Де U₀ - задана величина корисності.

Оптимальний портфель для типового інвестора визначається в результаті накладення його карти байдужості на безліч ефективного вибору; на рис. 5.6 її представляє точка Я. Алгебраїчна модель і числовий приклад визначення оптимальної структури портфеля з п акцій наведені в математичному додатку до даної глави.

Мал. 5.6. оптимальний портфель

Мал. 5.5. Функція корисності типового інвестора

1. Податкова політика, компроміс між інфляцією і податковим тягарем
   Уряд дотримується ліберальної економічної політики і прагне скоротити інфляцію і податковий тягар. Цільова функція уряду - квадратична функція темпу інфляції (л) і податкових надходжень (Г), в якій суб'єктивним параметром служить значимість інфляції щодо податкових надходжень (а): Обмеження
2. Плюси і мінуси перехідної економіки
   До кінця 1980-х рр. стало ясно, що необхідні кардинальні реформи економічної системи. Адміністративно-командна економіка більш не могла забезпечити економічне зростання країни. Падіння виробництва, інвестицій, особистого споживання наростало, а інфляційний тиск на ціни внаслідок поглиблення
3. Планування і прогнозування рівня життя населення, система показників рівня життя в прогнозних дослідженнях
   В результаті вивчення даного розділу студент повинен: знати основні показники, що характеризують добробут населення, а також рівень і якість життя; інструментарій та технологію прогнозних розрахунків динаміки доходів і спожито і я населення; вміти аналізувати, узагальнювати і систематизувати
4. Перші кредитні цикли
   Ритми бувають різні. У 1909 р хітом продажів був автомобіль Ford-T. За рік продали 10 тис. Машин. Знадобилося сім років, щоб річний обсяг досяг 500 тис. Чи повториться через століття історія з люксовим електромобілем Tesla ? У 2013 р було продано 10 тис. Машин. Корпорація впевнена, що через
5. Перерозподіл доходу між населенням і державою
   «Нам потрібна інфляція 6% в найближчі роки. Це поліпшить ситуацію з боргами, передає агентство Bloomberg слова колишнього головного економіста МВФ, нині професора Гарвардського університету Кеннета Рогоффа. За прогнозами Білого дому, бюджетний дефіцит досягне 1,84 млрд дол. США в цьому фіскальному
6. Пастка ліквідності
   Останнім часом термін «пастка ліквідності» використовується для опису ситуації, в якій опинилися багато країн після 2008 р .: центральні банки знизили процентні ставки практично до нульового рівня, а економіка відмовляється реагувати на такі сигнали. У ряді випадків ситуації, що підпадають
7. Особливості біржових циклів
   Біржі постійно генерують різноманітні і часто взаємно протилежні імпульси. Ринок інформує про свій стан різними індикаторами, серед яких провідними є ціни. За кілька століть трейдери напрацювали різні правила поведінки і склали цілі торговельні системи, а економісти запропонували теорії для
8. Основні принципи побудови національної моделі link
   Модель LINK для національної економіки будується на основі відповідних баз даних. Існує можливість побудови моделей, пристосованих до індивідуальних особливостей економіки кожної окремої країни і наявними даними. У деяких країнах є в певній мірі однакові бази даних, але правильно зрозуміти