| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Людський капітал - якості людини, придбані в процесі освіти або кваліфікованої праці і служать джерелом доходу. В даному підпункті розглядається загальний людський капітал} який формується в процесі навчання в навчальному закладі.
В економіці є два сектори. Перший - традиційний, він виробляє ВВП, або дохід (У), використовуючи фізичний капітал (К), некваліфіковану працю (L) І людський капітал (Я):

Другий сектор - сфера освіти. Він виробляє людський капітал, випуск якого залежить від величини держвидатків на освіту (G) і тривалості часу, виділеного домогосподарством на свою освіту (?):

Рівновага домогосподарства - ситуація, в якій максимальний сумарний дохід, отриманий домогосподарством в якості оплати простого праці та кваліфікованої праці:

де w - ціна простого праці; h - віддача від одиниці людського капіталу в формі кваліфікаційної надбавки за один рік навчання.
Домогосподарство максимізує дохід, розподіляючи ресурс вільного часу (Г) між працею і навчанням (?):

Рівновага досягається, коли дохід (6.24) максимальний при виконанні обмежень (6.23) і (6.25). Прирівняємо нулю похідні функції Лагранжа:
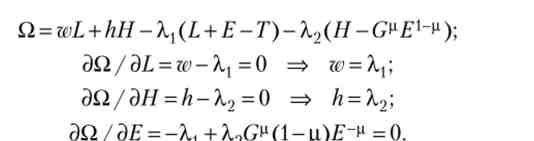
Підставами перше і друге рівності у третю, отримаємо:

З (6.26) випливає, що з ростом держвидатків па освіту зростає відношення ціпи простого праці до ціни людського капіталу і м е. знижується цінність платної освіти для домогосподарств. Перетворимо (6.23) і підставимо в (6.26), отримаємо:
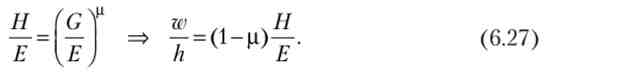
З (6.27) випливає, що з ростом тривалості освіти відношення ціни праці і віддачі від людського капіталу скорочується, т. з. частка надбавки за кваліфікацію в доході зростає. У конкурентній економіці ціни ресурсів рівні їх граничним продуктам (приватним похідним функції доходу). Висловимо ці ціни через дохід і розділимо вираження одне на інше:
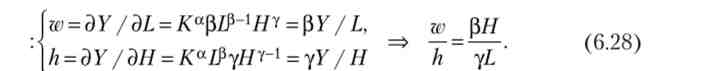
Умова рівноваги отримаємо, прирівнявши праві частини (6.27) і (6.28):
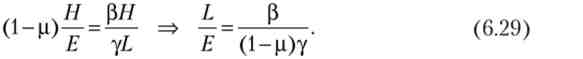
З (6.29) випливає, що рівноважна пропорція, в якій домогосподарство розподіляє ресурс часу між роботою і навчанням, визначається технологіями виробництва доходу (Р, у) і людського капіталу (р).
Досліджуємо динаміку людського капіталу при рівновазі домогосподарства. Логарифмуючи і диференціюючи (6.26), з огляду на, що ресурс часу розподілений оптимальним чином, а тому тривалість освіти незмінна (Е = 0):
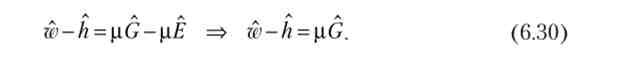
З (6.30) випливає, що ціна простого праці і віддача від людського капіталу зростають рівним темпом при сталості держвидатків на освіту. Якщо ці витрати зростають, то ціна праці зростає швидше, а якщо вони скорочуються, то вона росте повільніше, ніж надбавка за кваліфікацію. Логарифмуючи і диференціюючи вираження для w і h, отримані при виведенні формули (6.28). Віднімемо одне з іншого, припускаючи, що населення зростає темпом п:
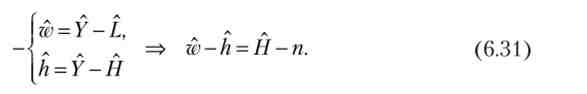
З (6.31) випливає, що ціна простого праці і віддача від людського капіталу зростають рівним темпом за умови, що обсяг людського капіталу і населення зростають рівним темпом. Якщо людський капітал зростає швидше населення, то ціна купа росте швидше, в іншому випадку вона росте повільніше, ніж віддача від освіти. Прирівняємо праві частини рівностей (6.30) і (6.31), отримаємо:

З (6.32) випливає, що при рівновазі домогосподарства темп приросту людського капіталу дорівнює сумі інтенсивної складової, пропорційної темпу приросту держвидатків на освіту, і екстенсивної складової, рівної темпу приросту населення. Якщо держвидатки і населення зростають, то людський капітал також зростає, якщо ж вони зменшуються, то людський капітал також убуває.
Стаціонарний зростання - ситуація, коли держвидатки на освіту, дохід і фізичний капітал зростають рівним темпом:

З (6.33) випливає, що при стаціонарному зростанні держава виділяє па освіту фіксовану частку ВВП. Прологаріфміруем і продифференцируем функцію доходу (6.22), потім перетворимо отриманий вираз з урахуванням (6.32) і (6.33), в результаті отримаємо і вирішимо рівняння щодо стаціонарного темпу економічного зростання (д):
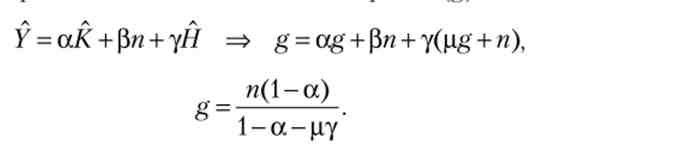
висновки: