| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Розглянемо фірму, в якій працівники використовують одну частину свого робочого часу на виконання трудових функцій, а іншу частину - на свої особисті цілі, т. Е. Вони «ухиляються» від роботи.
Коефіцієнт трудових зусиль (е) - частка робочого часу, що витрачається працівником на свої трудові функції; даний показник характеризує сумлінність працівника. Передбачається, що коефіцієнт трудових зусиль є функцією ставки зарплати і він прагне до одиниці при її прагненні до нескінченності:
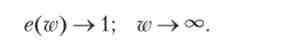
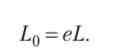
Фактичні витрати праці (10) - обсяг корисної праці, який служить аргументом виробничої функції фірми і дорівнює добутку коефіцієнта трудових зусиль і сплаченого обсягу робочого часу (L):
Прибуток фірми при одиничної ціни товару дорівнює різниці випуску (значення виробничої функції) і сумарною зарплати всіх працівників. На відміну від класичної моделі рівноваги фірми, прибуток тут залежить від двох аргументів - ставки зарплати і обсягу сплаченого праці «ухиляються» працівників:
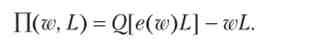
Рівновага фірми - ситуація, коли її прибуток максимальна.
Ефективна ставка зарплати в моделі фірми - ставка зарплати при рівновазі фірми. Ефективне значення трудових зусиль досягається при рівновазі фірми, воно менше максимально можливого значення, рівного одиниці.
визначимо умови рівноваги, прирівнявши нулю приватні похідні функції прибутку:
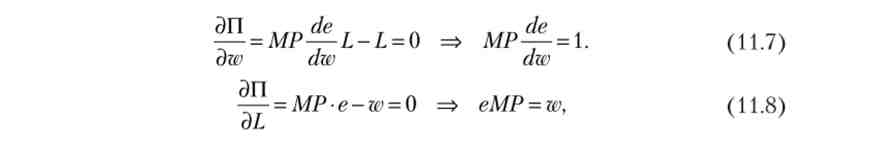
де МР - гранична продуктивність праці, або похідна виробничої функції.
Розділимо рівність (11.7) на рівність (11.8):
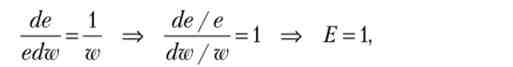
де Е - еластичність функції трудових зусиль е.
Ми прийшли до висновків:
Наведемо алгоритм визначення рівноваги фірми. По-перше, необхідно емпірично встановити функцію трудових зусиль і визначити аналітичним або геометричним способом ефективну ставку зарплати (ж? *), Що відповідає точці одиничної еластичності. Потім слід знайти ефективні значення коефіцієнта трудових зусиль (е*) І продуктивності праці:
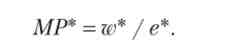
Оптимальна чисельність працівників фірми (L *) відповідає даним значенням граничного продукту праці.
приклад
Визначимо параметри рівноваги фірми, якщо виробнича функція - 2Z,05, функція трудових зусиль: е = 1 - 2 / w.
Про тсюда слід, що мінімальна ставка зарплати, починаючи з якої працівники докладають трудові зусилля, дорівнює 2. Дорівняємо одиниці формулу еластичності функції трудових зусиль:
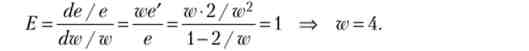
Ефективна ставка зарплати дорівнює 4, а ефективне значення коефіцієнта трудових зусиль дорівнює 0,5.
Ми розвиваємо мікромодель ефективної зарплати, описану в попередньому абзаці.
Коефіцієнт якості праці (е) - відношення корисного ефекту години робочого часу даного працівника до корисного результату години робочого часу абсолютно сумлінного, але некваліфікованого працівника:
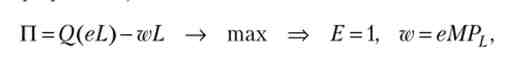
Працівники мають однакову функцію е, яка залежить від ставки зарплати в фірмі (W), ставки альтернативної зарплати в інших фірмах (wa) і рівня безробіття (І). Фірма максимізує прибуток, рівноважні значення ставки зарплати і чисельності персоналу називають ефективними. Прирівняємо нулю похідні прибутку за ставкою зарплати і витрат праці, отримаємо умови рівноваги фірми з мікромоделі (див. Підпункті 11.2.2):
де Е - еластичність функції e (w, zoa, і) за ставкою зарплати.
Звідси ефективна ставка не залежить від виробничої функції. Передбачається, що коефіцієнт якості праці може приймати нульові значення, він позитивний при певних умовах.
Порогова ставка зарплати (w0) - ставка зарплати, починаючи з якої якість праці позитивно. Вона залежить від альтернативної ставки зарплати рівня безробіття (І) і значущості безробіття (b > 0):

Порогова ставка не більше альтернативної ставки і прямо пропорційна їй, вона зростає з ростом рівня і значущості безробіття. Якщо порогова ставка дорівнює нулю, працівник готовий докладати якісь трудові зусилля при будь-якому рівні оплати праці. Така ситуація можлива, коли рівень безробіття настільки великий, що досягає зворотної величини до показника значущості безробіття (І = 1 / Ь). Якщо, наприклад, рівень безробіття дорівнює 20% при коефіцієнті значимості 5, то порогова ставка зарплати дорівнює нулю, оскільки 1 - 5 - 0,2 = 0.
Функція якості праці - залежність коефіцієнта якості праці (Е) від відносного перевищення фактичної ставки зарплати над її граничним значенням:

де р > 0.
З (11.10) випливає, що працівник ефективно працює (е > 1), коли ставка зарплати перевершує подвоєне значення порогової ставки (w > 2w0). Він «ухиляється» (0 < е < 1), коли ставка зарплати лежить в межах від однієї до двох значень порогової ставки (w0 < w < 2w0). Він взагалі не докладає трудових зусиль (е = 0), коли ставка зарплати нижче порогового значення (w < w0).
з умови Е = 1 для функції (11.10) висловимо ефективну ставку (w*) Через порогову:
З (11.11) випливає, що ефективна ставка більше порогової. У рівновазі вона дорівнює альтернативної ставкою, так як всі фірми в прагненні до рівноваги встановлять єдину ставку.
З рівностей (11.9) і (11.11) отримаємо ефективний рівень безробіття (І *):
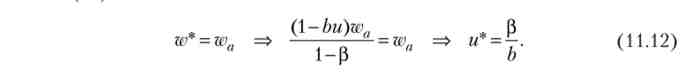
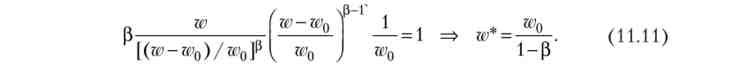
З (11.12) випливає, що ефективний рівень безробіття визначається суб'єктивними показниками і не залежить від виробничої функції, він росте при скороченні коефіцієнта значущості безробіття і при збільшенні чутливості якості праці до ставки зарплати. Таким чином, науково-технічний прогрес не впливає на динаміку безробіття. Підставами (11.11) і (11.12) в (11.10), отримаємо ефективну величину трудових зусиль:

З (11.13) випливає, що ефективні трудові зусилля залежать лише від еластичності функції трудових зусиль і не залежать від значущості для працівників фактора безробіття: