кредитне раціонування

Комерційний банк видає кредити і шукає таку ставку кредиту, яка забезпечить максимум його прибутку. Проблема полягає в тому, що при збільшенні ставки зростає прибуток, одержуваний від одного позичальника, але в той же час скорочується число самих позичальників, оскільки для деяких з них підвищена ставка не вигідна. Таким чином, вирішується незвичайна задача максимізації суми показників в умовах, коли число доданків є змінною величиною.

Кредитне раціонування - вибір банком ставки кредиту, яка максимізує прибуток в умовах, коли число позичальників банку залежить від ставки кредиту:

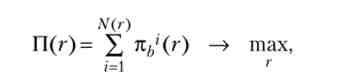
де П - сумарний прибуток банку; n_h'(R) - зростаюча функція прибутку банку, отриманої від г-го позичальника; г - ставка кредиту; N (r) - спадна функція кількості позичальників банку.

Нехай є кілька підприємців, які реалізують проекти з рівними інвестиціями В і рівним очікуваним доходом R, але з різним ступенем ризику. У разі успіху г-й підприємець отримує дохід Rf в разі невдачі - Rf (Однакова для всіх величина). Імовірність успіху - p_v невдачі - (1 - р,). Вважаємо, що зі збільшенням номера проекту зростає ймовірність успіху. Для всіх проектів виконується

Перетворимо цю рівність:

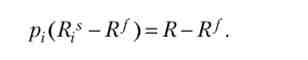
Звідси випливає, що чим більша ймовірність успіху проекту, тим менше дохід підприємця в разі успіху: оскільки всі проекти в середньому мають рівний дохід, збільшення одного «позитивного» фактора неминуче спричиняє скорочення іншого.

Банк видає кредит в розмірі В але своїй ставці г за умови, що при успіху підприємець виплачує кредит з відсотками (1 + г) У, а при невдачі - суму Rf, при цьому:

У разі невдачі прибуток підприємця дорівнює нулю, так як весь свій дохід Rf він віддає банку, тому очікуваний прибуток дорівнює

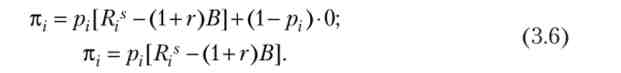
З (3.5) випливає, що очікуваний прибуток кожного підприємця більше нуля. підставами R,^s з (3.4) в (3.6), отримаємо прибуток підприємця як функцію ймовірності успіху:

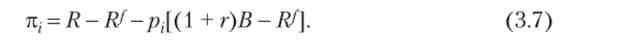
З нерівності (3.5) випливає, що очікуваний прибуток підприємця убуває з ростом p_iy т. е. фактор зниження доходу з ростом ймовірності успіху проекту виявився вирішальним.

Нормальна прибуток (я₀) - мінімальний прибуток підприємця, нижче якої реалізація будь-якого проекту невигідна.

відсікає ймовірність (Р) - максимальна ймовірність успіху підприємницького проекту, при якій прибуток не опускається нижче нормального рівня при заданому очікуваному доході проекту. Відтинає ймовірності відповідає відтинає (максимальний) номер проекту N. Для всіх реалізованих проектів виконується

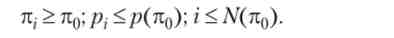
Очікуваний прибуток банку від i-го позичальника без урахування фактора дисконтування дорівнює очікуваному доходу за вирахуванням суми кредиту:

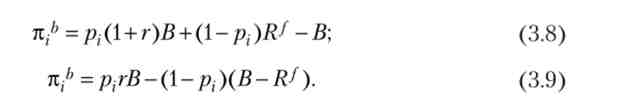
Звідси випливає, що прибуток банку від одного позичальника зростає лінійно з ростом ставки. Сумарний прибуток банку від N позичальників:

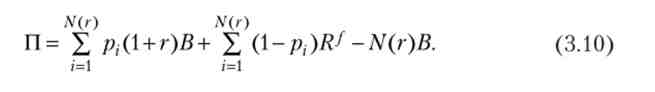
Досліджуємо зміни доданків у правій частині (3.10) з ростом г:

• перше може рости через зростання г або знижуватися через зниження N;
• другий знижується через зниження N, що спричиняє зниження прибутку;
• третій доданок негативне, його модуль знижується через зниження N, що спричиняє зростання прибутку.

Є дев'ять проектів: р, = 0,1; R = 3; Rf = В = 2. У табл. 3.3 значення R * розраховані за формулою (3.4), а значення до ,, при ставках 10% і 20% - за формулами (3.6) і (3.8). Досліджено прибуток банку при трьох значеннях мінімального прибутку і двох ставках відсотка. Якщо я_ц = 0,95, то при ставці 10% прибуток більше, ніж при 20% (0,06 > 0,04). Якщо я₀ = 0,91, то при ставці 10% прибуток також більше (0,2 > 0,12). Якщо я₀ = 0,71, то при ставці 10% прибуток менше (0,9 < 1,12). Отже, існує якесь значення мінімального прибутку підприємця, при якій банк отримує однакову прибуток при ставках 10% і 20%.

Таблиця 33

Кредитне раціонування: прибуток при різних ставках кредиту

Окремий випадок. є М проектів, а = 1 / М; р, = а г, RJ = В. Тоді з (3.4) і (3.6) слід

Отримаємо наближене (нецілим) значення відсікаючого номера проекту, прирівнявши прибуток її необхідної величини:

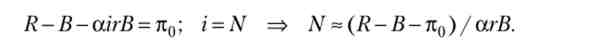
Надприбуток проекту (71)) - очікуваний дохід проекту за вирахуванням витрат (суми кредиту) і нормального прибутку (п_х = R - В - л₀). Тоді для розглянутого окремого випадку відтинає номер проекту дорівнює

Звідси випливає, що всі М проектів будуть вигідні, якщо надприбуток проекту перевищує виплати по кредиту (n_t > ГВ). В іншому випадку буде реалізована лише частина проектів.

З (3.9) отримаємо формулу прибутку банку від одного позичальника і загальний прибуток банку в разі, коли г л, / В і реалізуються всі М проектів. Використовуємо формулу суми арифметичної прогресії:

Звідси випливає, що при низьких ставках кредиту прибуток банку зростає пропорційно ставці кредиту. При високих ставках кредиту, коли г до, / В, реалізуються N проектів і прибуток банку дорівнює

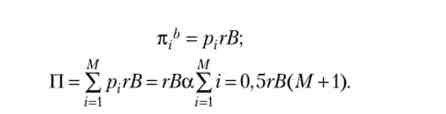
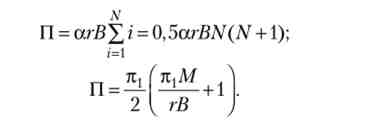
Звідси випливає, що при високих ставках кредиту прибуток банку падає з ростом ставки кредиту. Отже, оптимальна ставка кредиту (г *) дорівнює відношенню надприбутки від суми кредиту, а максимальна прибуток банку (II *) приблизно дорівнює половині сумарної надприбутки всіх проектів:

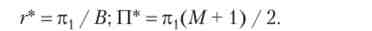
Прибуток банку спочатку зростає лінійно від нуля до максимального значення, а потім убуває по гіперболі з ростом ставки кредиту:

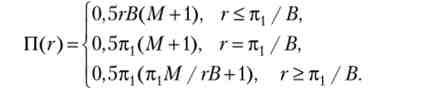
Безперервний випадок. Є безліч підприємців, функція щільності розподілу />, дорівнює &{Р,). якщо р - відсікає ймовірність, то формула прибутку банку (3.9) набуде вигляду

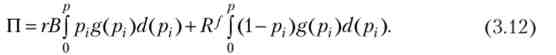
Продифференцируем (3.12), з огляду на, чтор залежить від г, і використовуючи правило диференціювання інтеграла із змінною верхньою межею. Прирівняємо похідну нулю:

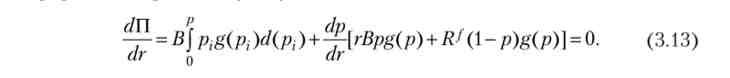
Інтеграл у правій частині позитивний, а другий доданок негативно, так як dp / dr < 0. Ставка кредиту, яка задовольняє (3.13), оптимальна для банку.

1. Модель ефективної заробітної плати Шапіро - Стігліца
   Корисність своєї угоди з підприємцем працівник представляє у вигляді різниці між одержуваної заробітної платою (W) і грошовою оцінкою своїх трудових зусиль, необхідних для її отримання (С). При несумлінному ставленні до праці (роботі з «прохолодою») С- 0, при сумлінному виконанні своїх обов'язків
2. Модель динаміки безробіття
   Передбачається, що граничні витрати найму одного робочого (МС) прямо пропорційні кількості найнятих працівників в одиницю часу (/ г), оскільки при збільшенні числа вакансій зазвичай зростає їх різноманітність і складність встановлення відповідності між працівниками і робочими місцями. Крім
3. Модель ак і конвергенція
   На відміну від моделі Солоу, де темп економічного зростання заздалегідь відомий, тут він є ендогенної величиною, т. Е. Визначається при аналізі моделі. Нехай чисельність населення (L) незмінна, тоді дохід залежить від обсягу капіталу (К) і ефективності праці (Е ): де b - продуктивність економіки.
4. Мікрофінансові організації
   З 2010 р з прийняттям Федерального закону від 02.07.2010 № 151-ФЗ «Про мікрофінансової діяльності та мікрофінансових організаціях», фінансовий простір Росії збагатилося ще одним активним суб'єктом - мікрофінансовими організаціями (МФО). Ці фінансові інститути надають кредити індивідуальним
5. Міжчасова оптимізація
   Модель поведінки репрезентативного споживача, описана нами вище, статична. Однак в ряді випадків є осмисленою завдання подивитися на поведінку споживача в динаміці. В цьому випадку репрезентативний споживач робить вибір щодо розподілу доходу за кілька періодів між споживанням і заощадженням
6. Метод ковзної середньої
   Заснований на обчисленні середніх величин за укрупнені періоди часу. Мета - абстрагуватися від впливу випадкових чинників, взаімопогасіть їх вплив в окремі роки. Для розрахунку використовують наступний алгоритм. 1. Визначають довжину інтервалу згладжування /, що включає в себе / послідовних
7. Метод аналітичного вирівнювання
   Цей метод (графи 6-8) заснований на обчисленні значень вирівняного ряду по відповідним математичних формул. Зазвичай в економічних дослідженнях застосовуються поліноми не вище 3-го порядку. Використовувати для визначення тренда поліноми високих ступенів недоцільно, оскільки отримані таким
8. Макромодель ефективної зарплати (Шапіро - Стігліц)
   Всі наймані працівники отримують рівну зарплату, але при цьому кожен працівник або сумлінно трудиться, або «ухиляється» від роботи, т. Е. На ринку праці є сумлінні і недобросовісні працівники. Сумлінний працівник витрачає фіксовані трудові зусилля, які ми вимірюємо величиною прожиткового мінімуму