| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Цей метод (графи 6-8) заснований на обчисленні значень вирівняного ряду по відповідним математичних формул. Зазвичай в економічних дослідженнях застосовуються поліноми не вище 3-го порядку. Використовувати для визначення тренда поліноми високих ступенів недоцільно, оскільки отримані таким чином аппроксимирующие функції будуть відображати випадкові відхилення, а це суперечить змісту тенденції.
Поліном першого ступеня yt = а0 + а}1; на графіку зображується прямою і використовується для опису процесів, що розвиваються у часі рівномірно.
Поліном другого ступеня yt = я0 + axt + а212 застосуємо в тих випадках, коли процес розвивається равноускоренно (т. е. є рівноприскореного зростання або равноускоренное зниження рівнів).
Як відомо, якщо параметр а2 > 0, то гілки параболи спрямовані вгору, якщо ж а2 < 0, то - вниз. параметри а0 і а{ не впливають на форму параболи, а лише визначають її положення.
Оцінки параметрів в обраної моделі визначаються методом найменших квадратів. Суть його полягає в знаходженні таких параметрів, при яких сума квадратів відхилень розрахункових значень рівнів від фактичних значень була б мінімальною. Таким чином, ці оцінки знаходяться в результаті мінімізації виразу:

де yt - дійсний рівень часового ряду; yt - розрахункове значення; п - довжина часового ряду.
Математичний апарат методу найменших квадратів докладно описаний в літературі з математичної статистики. Наведемо систему нормальних рівнянь, отриману в результаті мінімізації виразу:
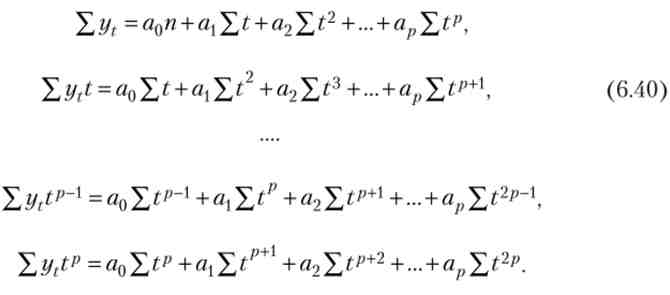
Система складається з (р + 1) лінійних рівнянь, що містять в якості невідомих величин (р + 1) коефіцієнтів а0, at, ар. Вирішення цієї системи дозволяє обчислити оцінки шуканих коефіцієнтів.
Системи для оцінювання полиномов невисоких ступенів мають більш простий вигляд. Наприклад, нормальні рівняння для оцінювання параметрів прямий (полінома першого ступеня yt = а0 + axt) мають вигляд

Вирішення цієї системи щодо шуканих параметрів дає наступні вирази:
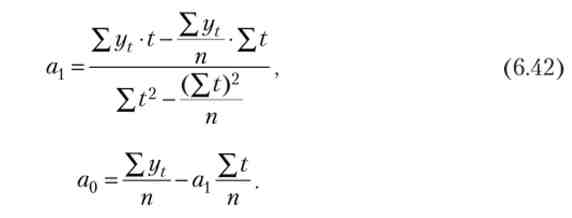
Для параболи 2-го порядку отримаємо аналогічну систему нормальних рівнянь
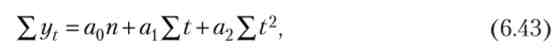
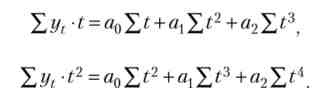
У табл. 6.10 приведені обчислення за рівнянням прямої лінії
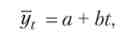
де yt - рівні вирівняного ряду (теоретичні показники); t - роки (1, 2, 3, і); а й h - невідомі параметри рівняння (аналогічні я0 і ах). Для визначення параметрів треба вирішити систему рівнянь
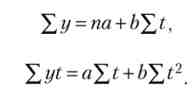
Необхідні величини для вирішення системи рівнянь обчислені і наведені в табл. 6.10 (графи 6-8), підставимо їх у рівняння
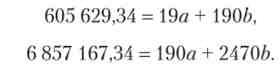
Розділимо обидві частини другого рівняння на 10 і отримаємо
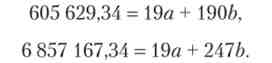
Звідси
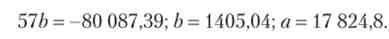
Отже, в результаті обчислень отримуємо а - 17 824,8; b = 1405,04. Підставами значення параметрів і отримаємо рівняння прямої
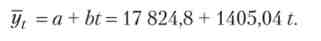
Для кожного року підставляємо значення t і отримуємо рівні вирівняного ряду (графа 9):

Зауважимо, що X # = XУt = 605 629,3.
У вирівняні ряду відбувається рівномірне зростання рівнів ряду в середньому за рік на 1405,04 млн руб. (значення параметру Ь). Метод заснований на абстрагуванні впливу всіх інших факторів, крім основного часу (рис. 6.1).
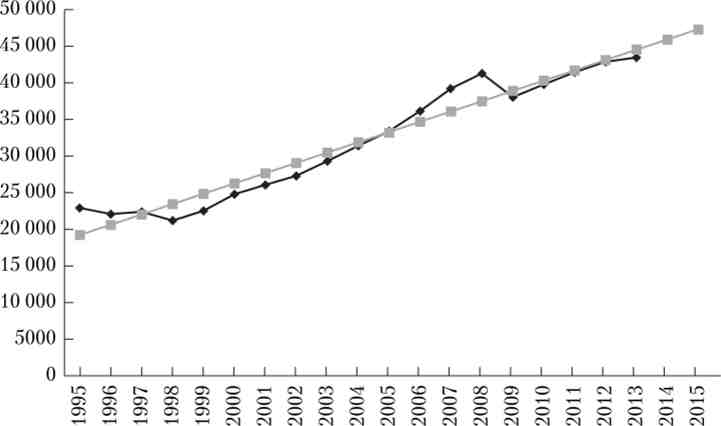
Мал. 6.1. Динаміка ВВП РФ за період 1995-2013 рр .:
ламана крива - фактичні дані; пряма лінія - згладжені дані, за якими був зроблений прогноз на 2014-2015 рр.
Явища можуть розвиватися в динаміці рівномірно (зростання або зниження). У цих випадках найчастіше використовується рівняння прямої лінії. Якщо ж розвиток нерівномірно, наприклад, спочатку дуже повільний ріст, а з певного моменту різке зростання або, навпаки, спочатку різке зниження, а потім уповільнення темпів спаду, то вирівнювання треба виконати за іншими формулами (рівняння параболи, гіперболи та ін.).
Для класу експоненційних кривих, на відміну від поліномів, характерною є залежність приростів від величини самої функції. Ці криві добре описують процеси, що мають «лавиноподібний» характер, коли приріст залежить від досягнутого рівня функції.
Проста експоненціальна (показова) крива має вигляд

якщо b> 1, то крива зростає разом з ростом t, і падає, якщо b < 1.
параметр а характеризує початкові умови розвитку, а параметр b - постійний темп зростання. Темп зростання дорівнює
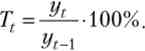
В даному випадку перетворення виглядає наступним чином:
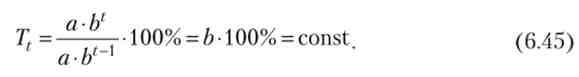
Відповідно, і темпи приросту постійні
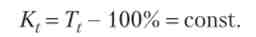
Можна показати, що логарифм ординати цієї функції лінійно залежить від?; для цього прологарифмируем вираз:

нехай In а = Л; In b = В. тоді In yt = А + tB.
Тепер, якщо тенденція ряду описується за допомогою моделі yt = ab, то для оцінювання невідомих параметрів можемо використовувати систему нормальних рівнянь для прямої. Інакше кажучи, нормальні рівняння будуються виходячи з мінімізації
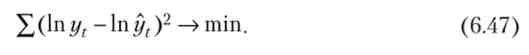
Відповідно, в нормальних рівняннях замість фактичних рівнів використовуються їх логарифми
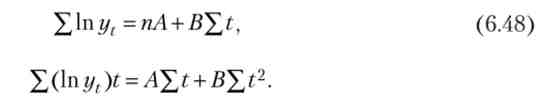
Знайдемо невідомі параметри А і В. Знаючи значення Л = 1пяіВ = 1пЬ, визначимо значення а і ред і за допомогою потенціювання одержимо показову функцію, що служить для вирівнювання ряду.
Такий підхід до оцінювання невідомих параметрів приваблює своєю універсальністю. Однак слід мати на увазі, що отримані оцінки параметрів виявляються зміщеними, так як при розрахунку беруть участь не вихідні рівні, а їх логарифми. Зсув буде тим значніше, чим більше різниця між послідовними рівнями динамічного ряду. До зміщення в подібних випадках не призводить нелінійний метод найменших квадратів.
Більш складним варіантом експоненційної кривої є логарифмічна парабола

Прологаріфміровав вираз, отримаємо параболу
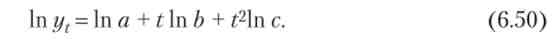
Таким чином, оцінку параметрів логарифмічною параболи можна знову отримати за допомогою методу найменших квадратів, використовуючи систему нормальних рівнянь для параболи. При цьому залишаються в силі зроблені вище зауваження про усунення отриманих оцінок.
Всі розглянуті типи кривих використовуються для опису монотонно зростаючих та відбувають процесів без «насичення».
Процес з «насиченням» слід описувати за допомогою кривої, що має відмінну від нуля асимптоту. Прикладом такої кривої може служити модифікована експонента

де у = k є горизонтальною асимптотой.
якщо параметр а негативний, то асимптота знаходиться вище кривої, якщо а позитивний, то нижче. При вирішенні економічних завдань найчастіше доводиться мати справу з кривою, у якій а < 0, b < 1. У цьому випадку зростання рівнів відбувається з уповільненням і прагне до деякого межі.
При вирішенні економічних завдань часто можна визначити значення асимптоти виходячи з властивостей прогнозованого процесу (наприклад, коефіцієнт використання обладнання не може перевищувати 1). Іноді значення асимптоти задається експертним шляхом. У цих випадках інші параметри кривої можуть бути визначені за допомогою методу найменших квадратів після приведення рівняння до лінійного вигляду

де до '- задане значення асимптоти.
Прологаріфміровав, можна для оцінювання параметрів In а і In b використовувати систему нормальних рівнянь.
Крім того, для оцінювання параметрів модифікованої експоненти можна використовувати як нелінійний метод найменших квадратів, так і ряд інших методів.
Таким чином, модифікована експонента добре описує процес, на розвиток якого впливає обмежуючий фактор, причому вплив цього впливу зростає разом з ростом досягнутого рівня.
Якщо вплив обмежує фактора починає позначатися лише після певного моменту (точки перегину), до якого процес розвивався по деякому експоненціальнимзакону, то для вирівнювання використовують S-образні криві.
Найбільш відомими з них є крива Гомперца і логістична крива (крива Перла - Ріда).
Рівняння кривої Гомперца має вигляд

Крива несиметрична.
Якщо log /, а < 0, крива має 5-подібний вид, при цьому асимптота, рівна до, проходить вище кривої.
Якщо log /, а> О, асимптота, рівна k, лежить нижче кривої, а сама крива змінюється монотонно: при b < 1 - монотонно убуває; при b> 1 - монотонно зростає.
Для вирішення економічних завдань найбільший інтерес представляє варіант цієї кривої, коли log /, а 0 і b 1.
Рівняння логістичної кривої виходить шляхом заміни в модифікованої експоненті у{ зворотною величиною 1 / yt

Використовується й інша форма запису рівняння логістичної кривої:

при t -»Ордината прагне до нуля, а при t -> 00 - до асимптоти,
що дорівнює значенню параметра k. Крива симетрична щодо точки перегину з координатами: t = In b : a; yt = k : 2.
Прогнозування, яке базується на екстраполяції, т. Е. На продовження в майбутнє тенденції, що спостерігалася в минулому, передбачає, що в часі ряду присутній тренд, характер розвитку показника володіє інерційністю, що склалася тенденція не повинна зазнавати істотних змін протягом періоду попередження.
Процедура розробки прогнозу з використанням кривих складається з наступних етапів:
В даний час в літературі описано кілька десятків кривих, багато з яких широко застосовуються для вирівнювання економічних часових рядів.
Криві умовно можна розділити на три класи в залежності від того, який тип динаміки розвитку вони добре описують.
До I класу відносяться функції, які використовуються для опису процесів з монотонним характером тенденції розвитку і відсутністю меж зростання. Ці умови справедливі для багатьох економічних показників, наприклад, для більшості натуральних показників промислового виробництва.
До II класу належать криві, що описують процес, який має межу зростання в досліджуваному періоді. З такими процесами часто стикаються в демографії, при вивченні потреб у товарах і послугах (у розрахунку на душу населення), при дослідженні ефективності використання ресурсів і т. д. Прикладами показників, для яких можуть бути вказані межі зростання, є середньодушове споживання певних продуктів харчування, витрата добрив на одиницю площі і т. п. Функції, що відносяться до II класу, називаються кривими насичення.
Якщо криві насичення мають точки перегину, то вони відносяться до III класу кривих зростання - до 5-образним кривим. Ці криві описують як би два послідовних лавиноподібних процесу (коли приріст залежить від вже досягнутого рівня): один з прискоренням розвитку, інший - з уповільненням.
Кожен з трьох розглянутих методів має свої переваги, але в більшості випадків метод аналітичного вирівнювання кращий. Однак його застосування пов'язане з великими обчислювальними роботами: рішення системи рівнянь; перевірка обґрунтованості обраної функції (форми зв'язку); обчислення рівнів вирівняного ряду; побудова графіка. Для успішного виконання таких робіт доцільно використовувати комп'ютер і відповідні програми.
Експоненціальне згладжування - метод згладжування часового ряду, який використовується для зменшення іррегулярності (випадкових коливань) часового ряду, що дозволяє отримати більш чітке уявлення про що лежать в основі цього ряду закономірності. Використовується також для прогнозування значення ряду (для 1-2 кроків прогнозу).