| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Кореляційний аналіз є одним з методів статистичного аналізу взаємозалежності декількох ознак - компонент випадкового векторах. Основне завдання кореляційного аналізу полягає в оцінці ступеня залежності між випадковими величинами. Коли говорять, що дві випадкові змінні корельовані, мають на увазі, як правило, що вони один з одним якось пов'язані. Стандартною мірою зв'язку змінних є коефіцієнт кореляції. Слід, однак, пам'ятати, що він вимірює лише силу лінійного зв'язку.
Коефіцієнт кореляції змінюється в межах від -1 до 1 і вимірює ступінь лінійного зв'язку двох випадкових змінних. Позитивне значення коефіцієнта кореляції означає, що із зростанням однієї з змінних інша також зростає, зі зменшенням однієї з них зменшується і інша. Негативне значення означає, що із зростанням однієї з змінних інша убуває, до убування однієї з них інша зростає. Коефіцієнт кореляції, що дорівнює 0, означає, що між змінними відсутній лінійного зв'язку. Зверніть увагу: навіть якщо коефіцієнт кореляції дорівнює 1 по абсолютній величині і, отже, змінні функціонально пов'язані (лінійно), нічого не можна сказати про причинно-наслідкового зв'язку між ними.
У статистичній практиці використовуються два коефіцієнти кореляції: для числових змінних - коефіцієнт кореляції Пірсона, для рангових - коефіцієнт кореляції Спірмена.
Ступінь лінійної залежності між кількісними змінними характеризується за допомогою парних, приватних і множинних коефіцієнтів кореляції і детермінації.
Парний коефіцієнт кореляції характеризує тісноту лінійної залежності між двома змінними на тлі дії всіх інших показників, що входять в модель.
Приватний коефіцієнт кореляції характеризує тісноту лінійної залежності між двома змінними при виключенні впливу всіх інших показників, що входять в модель. Дані коефіцієнти кореляції змінюються в межах від -1 до 1, причому чим ближче коефіцієнт кореляції до 1, гем сильніше залежність між змінними. Якщо коефіцієнт кореляції більше 0, то зв'язок позитивна, а якщо менше нуля - негативна.
Множинний коефіцієнт кореляції характеризує тісноту лінійного зв'язку між однією змінною (результативної) і іншими, що входять в модель; змінюється в межах від 0 до 1. Квадрат множинного коефіцієнта кореляції називається множинним коефіцієнтом детермінації. Він характеризує частку дисперсії однієї змінної (результативної), обумовленої впливом всіх інших змінних (аргументів), що входять в модель.
Вихідною для аналізу є матриця розмірністю (п - k), i-я рядок якої характеризує i-e спостереження (об'єкт) за всіма k-м показниками (7=1,2,..., к):

У кореляційному аналізі матрицю X розглядають як вибірку обсягу п з ^ -мірною генеральної сукупності, що підкоряється ^ -мірним нормальному закону розподілу. За вибіркою визначають оцінки параметрів генеральної сукупності: вектор середніх (х), вектор середньоквадратичних відхилень s і кореляційну матрицю (R) порядку (k - k)
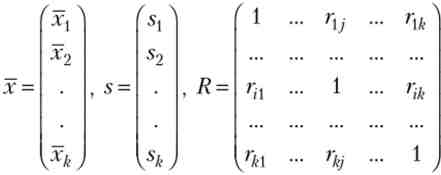
матриця R є симетричною 0} / = г ^ -) і позитивно певної:
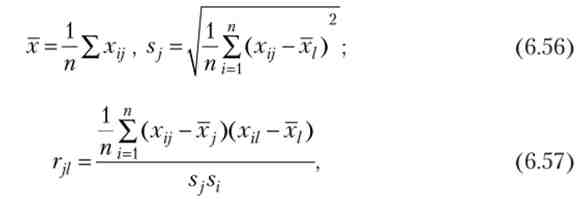
де Xjj - значення i-го спостереження j-ro фактор А; r}j - вибірковий парний коефіцієнт кореляції, характеризує тісноту лінійного зв'язку між показниками х-} і Xj. При цьому Гц є оцінкою генерального парного коефіцієнта кореляції.
Крім того, знаходяться точкові оцінки приватних і множинних коефіцієнтів кореляції будь-якого порядку. Наприклад, приватний коефіцієнт кореляції (До - 2) -го порядку між факторами Х( і Х2 дорівнює
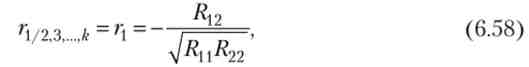
де Rji - алгебраїчне доповнення елемента Гц кореляційної матриці R. При цьому Rji = (-1 ) J+I мц, де М; / - мінор, визначник матриці, одержуваної з матриці R шляхом викреслювання j-й рядки і / -го стовпчика.
Множинний коефіцієнт кореляції (k - 1) -го порядку фактора (результативної ознаки) Xt визначається за формулою

де R - визначник матриці R.
Для простоти розгляду розподілу економічних показників за основу розгляду генеральної сукупності приймається двовимірний нормальний закон розподілу, який можна записати в такий спосіб:
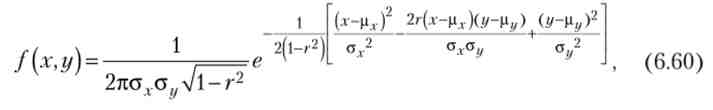
де |хх, р/ у - математичні очікування відповідно випадкових величин X і У; Gr,Gz / - середні квадратичні відхилення цих величин; г - коефіцієнт кореляції X і У.
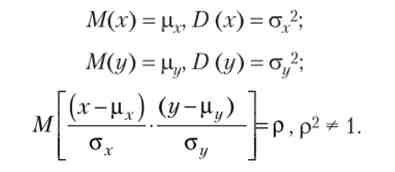
При даних параметрах можна отримати рівняння ліній регресії, що показують зміну умовних математичних очікувань в залежності від зміни відповідних значень випадкових аргументів:
М (у / г) - му = Рух(Х-МХ) - лінійне рівняння регресії у на х
М (у / г) - Мх = рху(У-Му) - лінійне рівняння регресії х на у
а//
Pwr= Р- - коефіцієнт регресії у на х;
° х
а
Рг... = Р ^ - - коефіцієнт регресії х на у.
J про
У
Квадрат коефіцієнта кореляції р2, т. е. коефіцієнт детермінації, в даній моделі вказує частку дисперсії однієї випадкової величини, зумовлену варіацією інший. Коефіцієнт регресії Р// Л показує, на скільки одиниць свого виміру збільшиться (Р > 0) або зменшиться (р < 0) в середньому у (М (у / х)), якщо х збільшити на одиницю свого виміру.
Завдання двовимірного кореляційного аналізу полягає перш за все в оцінці п'яти параметрів, що визначають генеральну сукупність.
Як точкових оцінок невідомих початкових моментів першого і другого порядку генеральної сукупності беруться відповідні вибіркові моменти.
Точкові ж оцінки невідомих інших параметрів отримують за допомогою формул, аналогічних формулам обчислення самих параметрів через генеральні початкові моменти. Таким чином, будемо мати: х - оцінка для jliv; х2 - оцінка для М (х2); у - оцінка для xlf у2 - оцінка для М (г /2); ху - оцінка для М (ху).
Відповідно, звідси
= х2 -(Х)2 - оцінка для ад.2; s2 - у2 -(У)2 - оцінка для ст/ у2; ху-ху
г = --- оцінка для р.
Оцінки генеральних коефіцієнтів регресії Р// Л. і РЛ / у виходять відповідно за формулами

Звідси оцінки рівнянь регресії мають вигляд
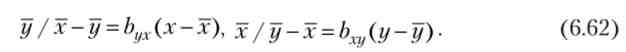
При цьому у / х і х / у - позначення оцінок для умовних математичних сподівань М (у / г) і М (х / у) генеральної сукупності.
Слід зазначити, що вищенаведені точкові оцінки є заможними, а х і у незміщеними і ефективними. Крім того, розподіл вибіркових середніх (х, у) не залежить від розподілу (S ?,
г). Вибірковий коефіцієнт кореляції г по абсолютній величині нс більше 1.