Споживання і пропозиція праці

Споживання, тягар праці та пропозиція праці

Один період часу. Домогосподарство максимізує корисність, що залежить від споживання і тягаря праці (/ а):

де с - споживання в годину; / - частка праці в загальному ресурсі часу; b - значимість тягаря праці щодо доходу (а> 1). Нетрудові доходи (дивіденди та ін.) Відсутні, тому споживання одно зарплати:

де 10 - ставка зарплати.

Знайдемо максимум (2.80) при обмеженні (2.81). Прирівняємо нулю приватні похідні функції Лагранжа і з системи рівнянь знайдемо рівноважну частку праці, або обсяг пропозиції праці:

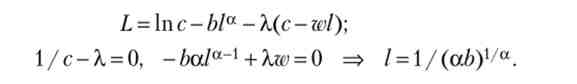
Отже, пропозиція праці залежить від коефіцієнтів а і b і в разі логарифмічною функції корисності доходу не залежить від ставки зарплати: ефекти доходу і заміщення компенсують один одного. Чим більше значимість тягаря праці, тим менше пропозицію праці. У загальному випадку пропозиція праці залежить від ставки зарплати.

приклад

Отримаємо функцію пропозиції праці, якщо U = з ° - И^а 0 < 1 < а. Прирівняємо нулю похідні функції Лагранжа і отримаємо шукану функцію:

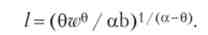
Так як 0 < а, пропозиція праці зростає з ростом ставки зарплати.

Два періоду часу. Домогосподарство максимізує дисконтовану корисність за два періоди, вважаємо 6 = 1:

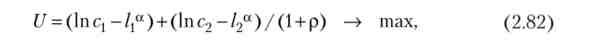
де q, з₂ - споживання; /₂ - частки праці в першому і другому періоді; р - міжчасового норма переваги, або суб'єктивна ставка дисконтування. Нетрудові доходи відсутні, а споживання у другому періоді одно зарплати плюс заощадження першого періоду з відсотками:

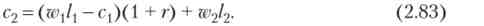
Розділимо (2.83) на 1 + г і отримаємо бюджетне обмеження:

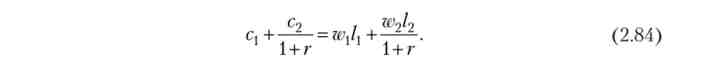
З (2.84) випливає, що дисконтовані за ставкою відсотка потоки споживання і зарплати рівні між собою. Оскільки в молодості домогосподарства роблять заощадження (або борги), то споживання в кожному періоді відрізняється від зарплати, т. Е. Обмеження (2.81) в даному випадку не виконується.

Знайдемо максимум (2.82) при обмеженні (2.84). Прирівняємо нулю похідну функції Лагранжа по і отримаємо функцію пропозиції праці в першому періоді:

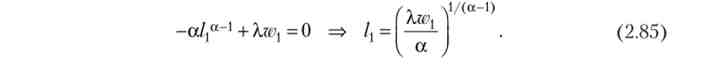
Прирівняємо нулю похідну функції Лагранжа по /₂ і отримаємо функцію пропозиції праці у другому періоді, потім з урахуванням (2.85) отримаємо відношення функцій пропозиції:

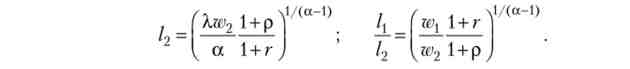
Отже, відношення обсягів пропозиції праці в першому і другому періоді збільшиться:

• з ростом ставки відсотка, так як з її ростом ростуть заощадження в першому періоді і споживання у другому періоді і, як наслідок, зростає інтегральна корисність;
• з ростом значущості поточного споживання щодо майбутнього, т. е. при зниженні норми дисконтування (р);
• з ростом ставки зарплати в першому періоді: з її ростом цінність, яку приносить одиницею праці в першому періоді, зростає відносно цінності, принесеної одиницею праці в другому періоді, що стимулює збільшення пропозиції праці в першому періоді.

При низької еластичності функції тягаря праці відношення обсягів пропозиції праці високо еластично по відносній ставкою зарплати. Нехай а = 1,1; г = р, тоді маємо: тоді при зростанні відносини ставок зарплати в першому періоді на 1% відношення обсягів пропозиції праці в цьому періоді зросте більш ніж на 10%, оскільки (1 + 0,01) = 1,1046.

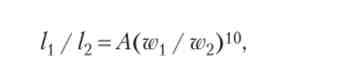
приклад

Визначимо оптимальну норму заощадження, коли пенсії немає, ставка відсотка нульова, функція корисності - статечна, а споживання в молодості залежить від тягаря праці:

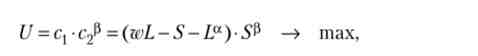
де (q = wL - S - L^a) - споживання в молодості; S - споживання в старості, або заощадження в молодості; L^a - тягар праці (а > 1); р - значимість споживання в старості. Прирівнявши нулю приватні похідні U, отримаємо:

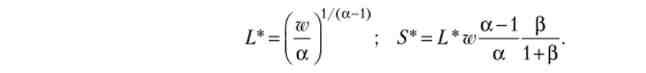
Звідси оптимальна норма заощадження дорівнює

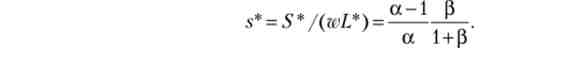
Отже, пропозиція праці (L *) не залежить від значимості споживання в старості, воно росте з ростом ставки зарплати і зниженням еластичності функції тягаря праці (а). Оптимальна норма заощадження зростає з ростом параметрів а і р.

Визначимо функцію пропозиції праці, якщо U = З ° + 6 (1 - /)⁽⁾; 0 < 1. Дорівнявши нулю похідні функції Лагранжа, отримаємо шукану функцію:

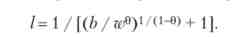
З ростом ставки зарплати пропозиція зростає, прагнучи до одиниці.

Два періоду часу. Домогосподарство максимізує дисконтовану корисність:

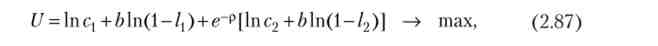
де q, з₂ - споживання; 1_і 1₂ - частки праці в першому і другому періоді; р - міжчасового норма переваги, або суб'єктивна ставка дисконтування. Нетрудові доходи відсутні.

Бюджетне обмеження - дисконтовані за ставкою відсотка (?) потоки споживання і зарплати дорівнюють

Знайдемо максимум (2.87) при обмеженні (2.88). Прирівняємо нулю похідні функції Лагранжа, отримаємо:

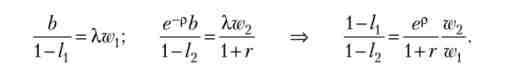
Отже, відношення обсягів дозвілля в першому і другому періоді зростає:

• зі зменшенням ставки відсотка, так як при цьому цінність заощаджень падає, що знижує стимули до праці в першому періоді;
• зі збільшенням значущості поточного споживання щодо майбутнього, т. е. з ростом р;
• зі збільшенням ставки зарплати в другому періоді, так як це зростання стимулює зростання пропозиції праці (скорочення дозвілля) в цьому періоді.

Отже, при даній функції корисності відношення обсягів пропозиції праці нс залежить від Ь, але залежить від ставок зарплати, ставки відсотка і межчасовий норми переваги. Воно не зміниться при пропорційному збільшенні ставок зарплати в обох періодах.

Загальний випадок. Домогосподарство максимізує дисконтовану корисність на нескінченному проміжку часу:

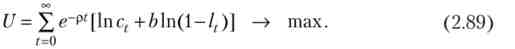
Споживання (с) дорівнює сумі незмінного нетрудового доходу (з₀) І зарплати (wl)

Вирішивши завдання (2.89) при обмеженні (2.90) методом Лагранжа, отримаємо функцію пропозиції праці:

З (2.91) випливають висновки:

• 1) обсяг пропозиції праці є функцією поточної ставки зарплати і не залежить від норми міжчасового переваги;
• 2) за відсутності нетрудових доходів (з₀ = 0) ми приходимо до отриманої раніше формулою / = 1 / {Ь + 1);
• 3) якщо праця і дозвілля мають рівну цінність (B = 1), а ставка зарплата незмінно дорівнює нетрудових доходів (w_t = з₀), Тоді пропозиція праці дорівнює нулю;
• 4) з ростом нетрудового доходу обсяг пропозиції праці падає;
• 5) відношення споживання до дозвілля прямо пропорційно ставці зарплати і обернено пропорційно цінності дозвілля. Перетворимо (2.91):

1. Теорія кредитного фонду
   Розбіжності між неокласиками і Кейнсом з питання про утворення ринкової ставки відсотка породили теорію кредитного фонду {Loanable funds theory ). Відповідно до неї ставка відсотка утворюється в результаті взаємодії попиту і пропозиції на ринку кредиту. Пропозиція кредиту є сума трьох доданків:
2. Теорія інфляції
   № 73 Число працюючих в стані повної зайнятості становить 64 млн чоловік; при цьому величина національного доходу досягає 360 млрд руб. Динаміка фактичної зайнятості (N) протягом 12-летіего періоду характеризується такими даними: Рік ... 1 2 3 4 5 6 7 8 9 10 11 12 N ... 64 70 68 60 58 58 70
3. Теорія економічних циклів, поняття економічного циклу
   Теорія економічних циклів поряд з теорією економічного зростання пояснює характер розвитку економіки в часі. Статистичні дані свідчать, що зміна показників, що характеризують результати національних господарств, змінюються не монотонно, а колебательно. На рис. 9.1 показані темпи приросту реального
4. Теоретичне обґрунтування зв'язку розвитку населення і кредиту
   Майже повсюдно нарощування кредитних комунікацій відбувалося під впливом зростання населення. Однак висхідний тренд кредиту періодично переривався і тимчасово відступав. Як тільки намічалося скорочення приросту і, тим більше, відбувалося падіння чисельності і щільності населення, кредитні
5. Технічний прогрес в галузі
   Погляди економістів на роль технічного прогресу в зміні фондовіддачі істотно розрізняються. Очевидно, в залежності від стадії розвитку галузі технічний прогрес може бути як фондосберегающім, так і фондомістким. Такі напрямки технічного прогресу, як збільшення одиничної потужності основних
6. Сукупний попит, найпростіша функція сукупного попиту
   У найпростішому випадку функцію сукупного попиту можна вивести з кількісного рівняння Нагадаємо, що М - екзогенно задана (державою) пропозиція грошей, а V - також екзогенно задана константа, яка відображає швидкість обігу грошей. Якщо у нас задана ліва частина кількісного рівняння, праву частину
7. Створення і знищення грошей банківською системою, центральний банк
   Основу всієї грошової маси країни складають банкноти і монети, тому їх називають грошовою базою. Банкноти надходять в обіг двома шляхами. По-перше, центральний банк розплачується ними при купівлі у населення або держави золота, іноземної валюти і цінних паперів. По-друге, він може надавати
8. Столітній механізм ціноутворення золота змінила електронна платформа
   20.03.2015 еталонні ціни на золото в злитках в Лондоні почали визначатися на електронному аукціоні ICE. Нова система прийшла на зміну історичному золотому фіксингу, який діяв з 1919 р 20.03.2015 на лондонській біржі ICE еталонна ціна золота в злитках, раніше відома як London Gold Fix, вперше