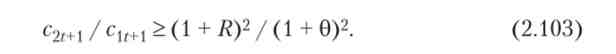
| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Альтруїзм - максимізація корисності в разі, коли вона залежить не тільки від обсягу споживання даного індивіда, але також від обсягів споживання деяких інших індивідів. Альтруїст свідомо скорочує своє споживання в їх користь не через якихось «вищих» міркувань, а тому, що в результаті його власна корисність зростає. Так, мати витрачає частину заробітної плати на збільшення добробуту своїх дітей, і в підсумку її добробут стає більше, ніж в разі використання ня всього доходу на свої особисті потреби.
Нехай альтруїзм властивий всім членам суспільства, і припустимо, що покоління, народжене в момент t, максимізує дисконтовану корисність свою і всіх наступних поколінь:
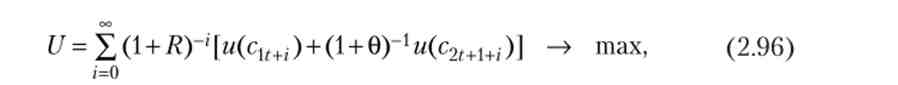
де cu + i, c2t ++j - споживання молодих і літніх, народжених в момент t + i; 0 - норма міжчасового переваги між корисністю споживання в молодості і старості; R > 0 - норма міжчасового переваги між корисністю споживання різних поколінь. Чим менше / ?, тим більше схильність людей до альтруїзму, а при нескінченно великих значеннях показника люди не враховують корисність майбутніх поколінь. Пенсії та доходу в старості немає.
Дохід «середнього» молодого дорівнює сумі зарплати (wt) І залишеного йому спадщини (bt), а витрати - сумі споживання (зі) і заощаджень (st)
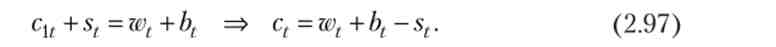
Споживання «середнього» похилого одно його заощадженням в молодості з відсотками (1 + rt + 1) st за вирахуванням залишеного ним спадщини (1 + п) Ь(+{ численнішим нащадкам (П - темп приросту населення):
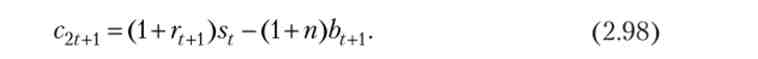
Вирішимо задачу максимізації (2.96) при обмеженнях (2.97) і (2.98). Підставами (2.97) і (2.98) в (2.96) і прирівняємо нулю похідну (2.96) по st. Враховуємо, що є лише два доданків в вираженні U, містять цю змінну:
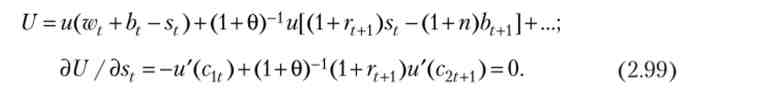
Прирівняємо нулю похідну (2.96) по Враховуємо, що є лише два доданків в вираженні U> містять цю змінну: одне зустрічається в попередній сумі, а друге - ні:
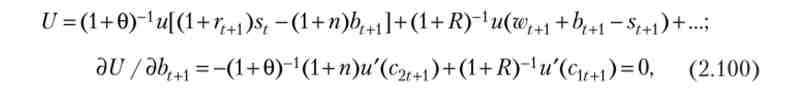
де зі + 1 - споживання дітей покоління, народженого в момент t.
Стаціонарний стан - споживання молодих (q), споживання літніх (з2) І ставка відсотка незмінні. У стаціонарному стані розділимо (2.99) на (2.100) і отримаємо
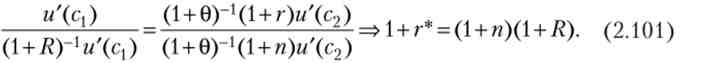
З (2.101) випливає, що при постійній чисельності населення суб'єктивна норма дисконтування повинна дорівнювати ставці відсотка (г * = R) Для досягнення максимуму дисконтированной корисності. При цьому умова рівноваги не залежить від норми міжчасового переваги між корисністю споживання в молодості і старості (0). Таким чином, наступ стаціонарного стану малоймовірно, оскільки воно задається екзогенними параметрами і не може досягатися за допомогою зміни обсягів споживання або спадщини.
Досліджуємо нерівноважні стану. З (2.100) випливає, що збільшення спадщини призведе до зростання дисконтированной корисності за умови
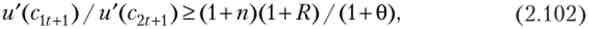
т. е. коли відношення граничних корисностей молодих і літніх перевершує якусь екзогенну величину. при і = з0*5 і постійному населенні умова (2.102) набуває вигляду:
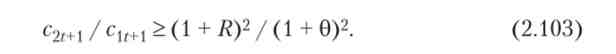
Оскільки відношення споживання літніх і молодих (ліва частина нерівності) зазвичай менше одиниці, для виконання нерівності необхідно, щоб права частина також була менше одиниці, т. Е. R < 0. Отже, збільшення розміру спадщини збільшує добробут при відносно низькому значенні / ?, т. Е. При високій схильності до альтруїзму.
З (2.99) випливає, що збільшення обсягу заощаджень призведе до зростання дисконтированной корисності за умови
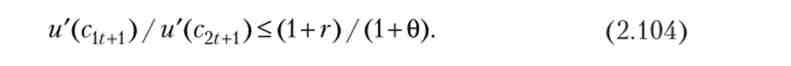
У разі функції і = з0*5 умова (2.104) набуває вигляду
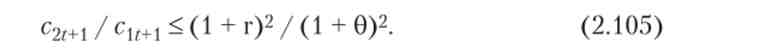
З (2.103) і (2.105) випливає, що при заданій функції корисності одночасне збільшення обсягів спадщини і заощаджень призведе до зростання дисконтированной корисності при виконанні умови:
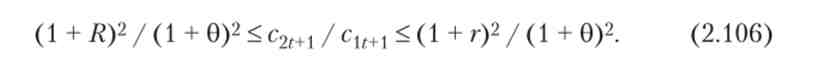
Дане подвійне нерівність сумісно за умови R г, т. е. при високих значеннях ставки відсотка і схильності до альтруїзму. У цьому випадку обсяги спадщини і заощаджень можуть нескінченно збільшуватися за рахунок того, що політика економії витрат в умовах високої ставки відсотка породжує лавиноподібне зростання накопичень.
приклади
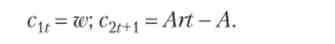
Споживання молодих незмінно, а споживання літніх і інтегральна корисність необмежено зростають з плином часу.