Ряди відносних величин

В економічній практиці дуже широко використовуються ряди відносних величин. Практично будь-який початковий ряд динаміки можна перетворити в ряд відносних величин. По суті перетворення означає заміну абсолютних показників ряду відносними величинами динаміки.

Для обґрунтованої оцінки розвитку явищ в часі необхідно обчислити аналітичні показники: абсолютний приріст, коефіцієнт зростання, темп зростання, темп приросту, абсолютне значення 1% приросту (табл. 6.7).

Таблиця 6.7

Основні показники динаміки часових рядів

До недоліків середнього абсолютного приросту і середнього темпу зростання (середнього темпу приросту) слід віднести те, що вони враховують лише кінцевий і початковий рівні ряду, виключають вплив проміжних рівнів. Проте ці показники мають широку сферу застосування, що пояснюється надзвичайною простотою їх обчислення. Вони можуть бути використані як наближені, найпростіші способи прогнозування, попередні глибшого кількісному і якісному аналізу.

У табл. 6.8 наведено числовий приклад, а нижче дані формули розрахунку і економічна інтерпретація показників.

Аналіз динаміки ВВП за період 2005-2012 рр. в цінах 2008 р,

млрд руб.

Абсолютні прирости (Ду) показують, на скільки одиниць змінився наступний рівень ряду в порівнянні з попереднім (графа 3 - ланцюгові абсолютні прирости) або в порівнянні з початковим рівнем (графа 4 - базисні абсолютні прирости). Формули розрахунку:

де Ду - абсолютний приріст (ДГ /^Ц - цінною, ДГ /^Г - базисний); у_п - рівень ряду за звітний період; г /_і_, - рівень ряду попереднього періоду; у₀ - початковий рівень ряду.

Коефіцієнт зростання показує, у скільки разів змінився рівень ряду в порівнянні з попереднім (графа 5 - ланцюгові коефіцієнти зростання або зниження) або в порівнянні з початковим рівнем (графа 6 - базисні коефіцієнти зростання або зниження). Формули розрахунку:

Темпи зростання показують, скільки відсотків становить наступний рівень ряду в порівнянні з попереднім (графа 7 - ланцюгові темпи зростання) або в порівнянні з початковим рівнем (графа 8 - базисні темпи росту). Формули розрахунку:

або

Темпи приросту показують, на скільки відсотків збільшився рівень звітного періоду в порівнянні з попереднім (графа 9 - ланцюгові темпи приросту) або в порівнянні з початковим рівнем (графа 10 - базисні темпи приросту). Формули розрахунку:

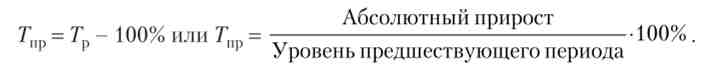
Якщо абсолютні рівні в ряду зменшуються, то темп буде менше 100% (темп приросту зі знаком мінус).

Абсолютне значення 1% приросту (графа 11) показує, скільки одиниць треба зробити в даному періоді.

Визначити абсолютне значення 1% приросту можна двома способами:

• 1) рівень попереднього періоду розділити на 100, щоб рівень попереднього періоду зріс на 1%;
• 2) ланцюгові абсолютні прирости розділити на відповідні ланцюгові темпи приросту.

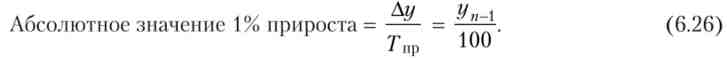
В динаміці, особливо за тривалий період, важливий спільний аналіз темпів приросту з вмістом кожного відсотка приросту або зниження.

Зауважимо, що розглянута методика аналізу рядів динаміки застосовна як для рядів динаміки, рівні яких виражені абсолютними величинами (кг, тис. Руб., Число працівників і т. д.), Так і для рядів динаміки, рівні яких виражені відносними показниками (% браку ,% зольності вугілля і ін.) або середніми величинами (середня врожайність в ц / га, середня заробітна плата і т. п.).

Поряд з розглянутими аналітичними показниками, обчислювальними за кожен рік в порівнянні з попереднім або початковим рівнем, при аналізі рядів динаміки необхідно обчислити середні за період аналітичні показники: середній рівень ряду, середній річний абсолютний приріст (зменшення) і середній річний темп зростання і темп приросту.

Розглянемо методи розрахунку середнього темпу зростання і середнього темпу приросту більш докладно на прикладі наведених в табл. 6.7 річних показників рівня ряду.

1. Сукупний попит, найпростіша функція сукупного попиту
   У найпростішому випадку функцію сукупного попиту можна вивести з кількісного рівняння Нагадаємо, що М - екзогенно задана (державою) пропозиція грошей, а V - також екзогенно задана константа, яка відображає швидкість обігу грошей. Якщо у нас задана ліва частина кількісного рівняння, праву частину
2. Сукупний попит і сукупна пропозиція
   В результаті вивчення матеріалу даного розділу студент повинен: знати обгрунтування використання рівняння кількісної теорії грошей як найпростішої моделі сукупного попиту; вплив макроекономічної політики держави на рух уздовж / зрушення кривої сукупного попиту; співвіднесення кривої сукупної
3. Сучасні тенденції світових ринків
   Основні напрямки галузевих зрушень, притаманних як в цілому світового господарства, так і окремим секторам і галузям світової економіки, пов'язані з наступними глобальними процесами. відбувається трансформація індустріальної економіки в постіндустріальну, з переважанням розвитку сектора послуг.
4. Структура ринку фінансів і система ставок відсотка
   Всю сукупність попиту і пропозиції фінансових активів, що утворить фінансовий ринок, можна розділити на два ринки: короткострокових кредитів і капіталу. на ринку короткострокового кредиту об'єктом купівлі-продажу є гроші центрального банку і цінні папери грошового ринку: короткострокові облігації
5. Столітній механізм ціноутворення золота змінила електронна платформа
   20.03.2015 еталонні ціни на золото в злитках в Лондоні почали визначатися на електронному аукціоні ICE. Нова система прийшла на зміну історичному золотому фіксингу, який діяв з 1919 р 20.03.2015 на лондонській біржі ICE еталонна ціна золота в злитках, раніше відома як London Gold Fix, вперше
6. Становлення макроекономічної теорії: коротка історична довідка
   За історії макроекономіки написано безліч книг 1, ми ж обмежимося коротким розглядом розвитку макроекономіки в змінюваному соціально-історичному контексті, не заглиблюючись далі XVIII ст. Можна сказати, що основні питання макроекономіки - питання зростання і розподілу - з'явилися в роботах
7. Стабілізаційна політика
   Оскільки кожне квазірівноважне стан економіки не є Парето-оптимальним, то природно виникає питання: як можна поліпшити макроекономічну кон'юнктуру? Згідно неокейнсианской теорії відповідь на це питання залежить від того, який тип квазірівноваги склався в даний момент. У стані класичної безробіття
8. Споживання та інвестиції, модель з параметрами (Тобін)
   Дохід - функція капіталу: Y = К а, інвестиції (Г) дорівнюють приросту капіталу (амортизації немає), витрати складаються з витрат на закупівлю і установку капіталу: С = (Р + з 1, де р - ціна нового капіталу; с - ціна його установки. Нехай ставка відсотка - м Прибуток в період t дорівнює різниці