Моментні ряди динаміки

Рівні моментних рядів динаміки характеризують стан досліджуваного явища в певні моменти часу. Кожен наступний рівень включає в себе повністю або частково попередній рівень. Так, наприклад, число працівників на 1 квітня 2013 р повністю або частково включає число працівників на 1 березня 2013 р

Якщо скласти ці показники, то отримаємо повторний рахунок тих працівників, які працювали протягом усього місяця. Отримана сума економічного змісту не має, це розрахунковий показник.

В моментних рядах динаміки з рівними інтервалами часу середній рівень ряду обчислюється але формулою середньої хронологічної

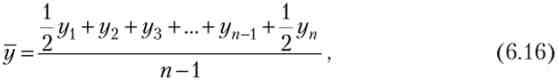
де у - рівні моментного ряду; п - число моментів (рівнів ряду); лг - 1 - число періодів часу (років, кварталів, місяців).

Розглянемо методику такого розрахунку за даними про облікової чисельності працівників підприємства за I квартал, наведеними в табл. 6.6.

Таблиця 6.6

Облікова чисельність працівників підприємства за I квартал

Необхідно обчислити середній рівень ряду динаміки, в даному прикладі - середню Облікова чисельність працівників підприємства:

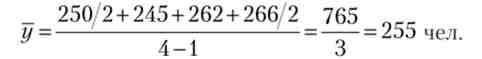
Розрахунок виконаний за формулою середньої хронологічної. Середня спискова чисельність працівників підприємства за I квартал склала 255 чол. У знаменнику - три місяці в кварталі, а в чисельнику - 765, це розрахункове число, економічного змісту не має. У переважній кількості економічних розрахунків місяці, незалежно від числа календарних днів, вважаються рівними.

В моментних рядах динаміки з нерівними інтервалами часу середній рівень ряду обчислюється за формулою середньої арифметичної зваженої. Як терезів середньої приймається тривалість часу (T - дні, місяці). Виконаємо розрахунок за цією формулою.

Облікова чисельність працівників підприємства за жовтень: на 1 жовтня - 200 чол., 7 жовтня прийнято 15 чол., 12 жовтня звільнений 1 чол., 21 жовтня прийнято 10 чол., І до кінця місяця прийому і звільнення працівників не було. Цю інформацію можна представити в наступному вигляді.

При визначенні середнього рівня ряду треба врахувати тривалість періодів між датами, т. Е. Застосувати формулу середньої арифметичної зваженої

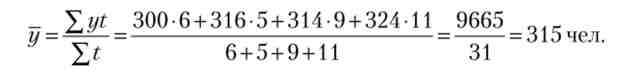
У цій формулі чисельник (Lyt) має економічний зміст. У наведеному прикладі чисельник (9665 людино-днів) - це календарний фонд часу працівників підприємства за жовтень. У знаменнику (31 день) - календарне число днів у місяці.

У тих випадках, коли маємо моментний ряд динаміки з нерівними інтервалами часу, а конкретні дати зміни показника невідомі досліднику, то спочатку треба обчислити середню величину (г /,) для кожного інтервалу часу за формулою середньої арифметичної простої, а потім обчислити середній рівень для всього ряду динаміки, зваживши обчислені середні величини тривалістю відповідного інтервалу часу (?,). Формули мають такий вигляд:

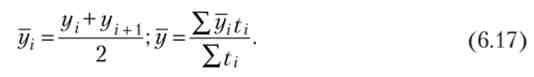
Розглянуті вище ряди динаміки складаються з абсолютних показників, одержуваних у результаті статистичних спостережень. Побудовані спочатку ряди динаміки абсолютних показників можуть бути перетворені в похідні ряди: ряди середніх і відносних величин. Ряди відносних величин можуть бути ланцюгові (у% до попереднього періоду) і базисні (в% до початкового періоду, прийнятому за базу порівняння - 100%). Розрахунок середнього рівня в похідних рядах динаміки виконується за іншими формулами.

Ряд середніх величин. Спочатку перетворимо Назнавств вище моментний ряд динаміки з рівними інтервалами часу в ряд середніх величин. Для цього обчислимо середню Облікова чисельність працівників підприємства за кожен місяць як середню з показників на початок і кінець місяця (У (): за січень (150 + 145): 2 = 147,5; за лютий (145 + 162): 2 = 153,5; за березень (162 + 166): 2 = 164. Уявімо це в табличній формі.

Середній рівень в похідних рядах середніх величин розраховується за формулою середньої аріфметічекой простий

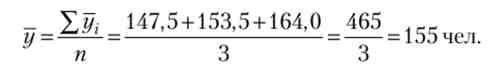
Зауважимо, що середня спискова чисельність працівників підприємства за I квартал, обчислена за формулою середньої хронологічної на базі даних на 1-е число кожного місяця і по середньої арифметичній - за даними похідного ряду - рівні між собою, т. Е. 155 чол. Порівняння розрахунків дозволяє зрозуміти, чому в формулі середньої хронологічної початковий і кінцевий рівні ряду беруться в половинному розмірі, а всі проміжні рівні - в повному розмірі.

Ряди середніх величин, похідні від моментних або інтервальних рядів динаміки не слід змішувати з рядами динаміки, в яких рівні виражені середньою величиною. Наприклад, середня врожайність пшениці по роках, середня заробітна плата і р д.

1. Огляд дискусії в зв'язку з моделюванням очікувань
   У зв'язку з гіпотезою раціональних очікувань обговорюється, якою мірою можна вважати економічних агентів дійсно раціональними. Критики раціональних очікувань відзначають, що багато економічні агенти (в першу чергу домогосподарства, окремі індивіди, а також ряд фірм) навряд чи відрізняються
2. Очікування і економічна політика
   В результаті вивчення матеріалу даного розділу студент повинен: знати поняття і найпростіші способи моделювання адаптивних очікувань; поняття раціональних очікувань; зміст критики Лукаса; передумови, учасників та їх ролі, основні ринки і основні висновки моделі Барро - Гордона; основні дискутованих
3. Обмеження державної політики
   Недоліки пасивної, неактівістской, державної політики очевидні: така політика пасивно слідує за подіями в економіці і не намагається реагувати на поточну ситуацію. На перший погляд здається, що це активистская політика, оскільки вона позбавлена подібних недоліків, є більш ефективною і доцільною.
4. Невизначеність на ринку праці, сигнали на ринку праці (Спенс)
   Сигнал - формальна ознака працівника, який побічно характеризує продуктивність його праці (освіта, стаж, вік) і в силу цього використовується роботодавцем як критерій при призначенні ставки зарплати працівника під час його найму. В теорії сигналів М. Спенса найважливішим фактором продуктивності
5. Неокласичний підхід
   У відповідності з поглядами класичної школи ринок сам по собі встановлює рівновагу між попитом і пропозицією. Регулюючої процедурою є процес змагання цін, який змінює і постійно оптимізує пропорції. В процесі вибору покупець постійно порівнює ціни / якість і вибирає оптимальні варіанти. Класична
6. Неокейнсіанські функції споживання та пропозиції праці
   Кількісні обмеження на ринках впливають не тільки на споживання і трудову активність домашнього господарства, а й на його збереження. Якщо індивід очікує, що в майбутньому зустрінеться з раціонуванням на ринку праці, то він буде зберігати більше, ніж тоді, коли очікує зустрітися з обмеженням
7. Найпростіші моделі сукупної пропозиції, кейнсіанські моделі сукупної пропозиції
   У попередньому параграфі ми вивели функцію сукупного попиту, що показує залежність загального попиту з боку всіх економічних агентів (репрезентативного споживача, репрезентативного виробника, держави) в залежності від рівня цін. В цьому і наступному параграфах ми розглянемо функцію сукупної
8. Національний баланс активів і пасивів., компоненти балансу активів і пасивів
   Баланс активів і пасивів: 1) враховує тип і вартість всіх фінансових і нефінансових активів і пасивів (боргів) економіки на початок і кінець року; 2) відображає зміни в чистій вартості капіталу та їх джерела, з чого складається «чисте багатство» країни. Дані про запаси основних фондів як частина