
| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
На практиці для кількісної оцінки динаміки процесів широко застосовуються такі основні аналітичні показники:
Причому кожен із зазначених показників може бути трьох видів:
В основі розрахунку цих показників динаміки лежить порівняння рівнів часового ряду. Якщо порівняння здійснюється з одним і гем же рівнем, прийнятим за базу порівняння, то ці показники називаються базисними. За базу порівняння вибирається або початковий рівень динамічного ряду, або рівень, з якого починається новий етап розвитку. Наприклад, при аналізі динаміки розвитку російської економіки за базу порівняння часто вибирають 2000 При здійсненні досліджень короткострокового характеру за базу порівняння можна взяти 2010 г. Слід зазначити, що для більш повної картини розвитку російської економіки слід починати розрахунки з 1990 р Це істотно подовжує тимчасової ряд, але дозволяє більш повно представити картину розвитку економіки країни.
У ряді випадків цей вибір може істотно відбитися на трендах. Це пов'язано з тим, що до 1987 р в багатьох галузях промисловості спостерігався уповільнює підйом, який перейшов потім у спад виробництва. Тому що почався в посткризовий період піднесення виробництва бажано оцінювати не тільки по відношенню до попереднього року, але і в порівнянні з 1990 р У російській практиці нерідко за базу приймаються 2003 2008 років., Так як Росстат здійснює приведення цін в постійні, приймаючи за постійні ціни даних років.
Якщо порівняння здійснюється за змінної базі і кожний наступний рівень порівнюється з попереднім, то обчислені таким чином показники називаються ланцюговими.
Середній аналітичний показник найбільш часто використовується в практиці систематизації даних та їх прогнозу. Деякі узагальнюючі характеристи дозволяють глибше зрозуміти особливості об'єкта спостереження. До них відноситься перш за все середнє значення ознаки, навколо якого варіюють інші його значення. Розрізняють декілька видів середніх величин: середнє арифметичне, мода, медіана і т. д.
Середнє є абстрактна типова характеристика всієї сукупності. Воно усуває, гасить, згладжує випадкові і невипадкові коливання, вплив індивідуальних особливостей і дозволяє уявити в одній величині деяку загальну характеристику реальної сукупності одиниць.
Серед усього різноманіття середніх практично найбільш часто використовується середнє арифметичне. Середнє арифметичне (х) є частка від ділення суми всіх значень ознаки на їх число:
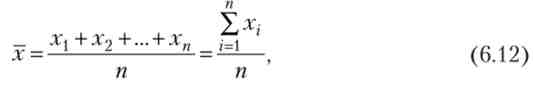
де х{ - значення ознаки; п - число об'єктів.
Найпростішою із заходів центральної тенденції є мода (Мо). Мода - це таке значення в сукупності спостережень, яке зустрічається найчастіше. Для номінальних змінних мода - це єдиний спосіб вказати найбільш типове, поширене значення. Зрозуміло, дослідник може користуватися модальним значенням і для характеристики розподілу змінних, виміряних на більш високому рівні, якщо для цього існують змістовні підстави (наприклад, описуючи розподіл відповідей на питання про кількість виписуються журналів).
В інтервальному ряду (з рівними інтервалами) модальним є клас з найбільшим числом спостережень. Значення моди знаходиться в його межах і обчислюється за формулою
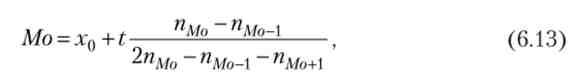
де Xq - нижня межа модального інтервалу; t - величина інтервалу; пМо ~ частота модельного інтервалу; пМо_{ - частота інтервалу, предшеству- ющего модальному; пМо +] - частота інтервалу, наступного за модальним.
медианой називається значення ознаки тієї одиниці сукупності, яка розташована в середині ряду частотного розподілу. В інтервальному ряду з різними значеннями частот обчислення медіани розпадається на два етапи: спочатку знаходять медіанний інтервал, якому відповідає перша з накопичених частот, що перевищує половину всього обсягу сукупності, а потім знаходять значення медіани за формулою
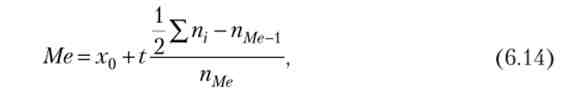
де х0 - нижня межа медіанного інтервалу; t - величина інтервалу; ni - частота інтервалу i пме_х - накопичена частота до медіанного інтервалу; пме - частота медіанного інтервалу.
Таким чином, медіана вибірки - це точка, з обох боків якої розташовується однакове число елементів вибірки. Якщо обсяг вибірки - непарне число і дорівнює 2п + 1, то медіана дорівнює елементу варіаційного ряду з номером п + 1. Якщо обсяг вибірки - парне число і дорівнює 2п, то медіана дорівнює напівсумі елементів варіаційного ряду з номерами піп + 1.
Для непарного числа даних, наприклад 23, маємо:
Дані: 96 48 27 72 39 70 7 68 99 36 103 95 4 6 13 34 74 1 65 42 28 54 69 Варіаційний ряд 14 6 7 13 27 28 34 36 39 42 48 54 65 68 69 70 72 74 95 96 99 103
Медіана дорівнює 48, 10 значень розташуються вище неї, і 10 - нижче.
Для парного числа даних, наприклад 22, маємо:
Дані: 57 55 85 24 33 49 94 2 8 51 71 30 91 6 47 50 65 43 41 73 Варіаційний ряд 2 3 6 7 8 24 30 33 41 43 47 49 50 51 55 57 65 71 85 91 94 96
Медианой є середнє двох «серединних» точок, в даному випадку середнє між 47 і 49, т. Е. 48.
Медіана розподілу - це точка т, обумовлена аналогічним умовою: ймовірність того, що випадкова величина прийме значення, що не перевершує т, дорівнює 1/2. Медіана вибірки є оцінкою медіани розподілу.
Доцільність використання того чи іншого типу середньої величини залежить, але принаймні, від наступних умов:
Метод розрахунку середніх залежить від типу ряду, в якому здійснюється розрахунок.
Середній рівень в інтервальних рядах динаміки (у) Обчислюється за формулою середньої арифметичної простої:

де у - рівні ряду (yv у2,..., уп), П - число періодів (число рівнів ряду).