Компоненти часових рядів

У практиці дослідження динаміки явищ і прогнозування прийнято вважати, що значення рівнів часових рядів економічних показників можуть містити такі компоненти (складові частини або структурно-утворюють елементи) (табл. 6.5):

• тренд;
• сезонну компоненту;
• циклічну компоненту;
• випадкову складову.

під трендом розуміють зміна, що б загальне напрям розвитку, основну тенденцію часового ряду. Це систематична складова довгострокової дії.

Поряд з довготривалими тенденціями у тимчасових рядах економічних процесів часто виникають більш-менш регулярні коливання - періодичні складові рядів динаміки.

Якщо період коливань не перевищує одного року, то їх називають сезонними. Найчастіше причиною їх виникнення вважаються природно-кліматичні умови. Прикладом можуть служити коливання цін на сільськогосподарську продукцію, зокрема на картоплю. З року в рік спостерігаються зниження цін в період після збирання врожаю і подальше підвищення цін, пов'язане з необхідністю зберігання продукції. Свого піку ціни досягають перед наступним врожаєм. Таким чином, в коливаннях цін простежується стійка річна періодичність.

Іноді причини сезонних коливань мають соціальний характер, наприклад збільшення закупівель в передсвятковий період, збільшення платежів наприкінці кварталу і т. д. При більшому періоді коливання вважають, що в тимчасових рядах має місце циклічна складова. Прикладами можуть служити демографічні, інвестиційні та інші цикли. Якщо з тимчасового ряду видалити тренд і періодичні складові, то залишиться нерегулярна компонента. Економісти поділяють чинники, під дією яких формується нерегулярна компонента, на два види:

• фактори різкого, раптового дії;
• поточні фактори.

Фактори першого виду (наприклад, стихійні лиха, епідемії та ін.), Як правило, викликають більш значні відхилення. Іноді такі відхилення називають катастрофічними коливаннями.

Фактори другого виду викликають випадкові коливання, які є результатом дії великої кількості побічних причин. Вплив кожного з поточних факторів незначно, але їх сумарний вплив може виявитися сильним.

Таблиця 6.5

Фактори, що впливають на значення часового ряду

Якщо часовий ряд представляється у вигляді суми відповідних компонент, то отримана модель називається адитивної (Вираз (6.1)), якщо у вигляді твору - мультипликативной (Вираз (6.2)) або змішаного типу (Вираз (6.3)):

де y_t - рівні тимчасового ряду; u_t - трендова складова; s_t - сезонна компонента; v_t - циклічна компонента; e_t - випадкова компонента.

У практиці досліджень використовується досить широке коло функціональних залежностей між змінними. Основні з них такі:

1) лінійна

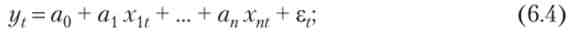
2) права напівлогарифмічний

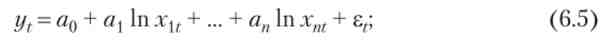
3) статечна

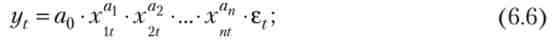
4) гіперболічна

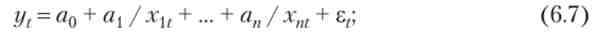
5) логарифмічна гіперболічна

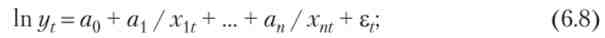
6) зворотна лінійна (функція Торнквиста)

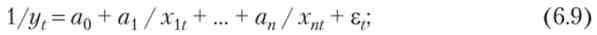
7) функція з постійною еластичністю заміни 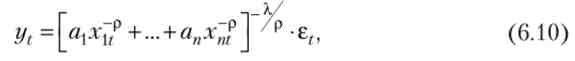де X і р - також параметри функції.

Слід зазначити, що в практичних дослідженнях можуть зустрітися і комбінації розглянутих вище залежностей. наприклад,

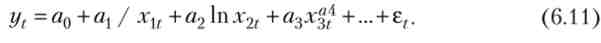
Тут необхідно зазначити, що значна більшість функцій за допомогою певного набору перетворень можуть бути приведені до лінійної формі (вираз 6.4). Наприклад, якщо у і x_i пов'язані залежністю у ~ / г_{ (Вираз 6.8.), То, ввівши змінні = 1 / г_ь отримаємо вираз 6.5 з точністю до перетворення вихідних факторів.

Аналогічним чином, використовуючи перетворення - In x_v отримаємо лінійну модель при логарифмічною взаємозв'язку між змінними у і Xj, т. е. у ~ In Xj.

1. «Літо», «Осінь»
   За навесні слід літо. Перехід відбувається непомітно, але коли він завершується, то сезон в розпалі. Влітку вся увага зосереджується на врожаї: вчасно полити, прибрати бур'яни, прополоти, уберегти від зайвої вологи і надмірного сонця. Точно так само і в економіці: кредити та інвестиції підтримують
2. Лінійна функція, функція Аллена
   передумови: а) граничні продуктивності факторів постійні і в нулі функція приймає нульове значення; б) гранична продуктивність одного з факторів постійна і функція однорідна першого ступеня в) функція однорідна і еластичність заміни факторів по Аллену нескінченна г) еластичності випуску за
3. Крива пропозиції заощаджень
   Нехай споживається один товар, тоді дохід і споживання домогосподарств виражаються в одиницях цього товару. Дохід в молодості дорівнює е і в старості - е 2, З х і З 2 - обсяги споживання в молодості і старості, Р { і Р 2 - ціни товару в молодості і старості (рівні цін). Бюджетне обмеження
4. Критерій парето і домінуючі стратегії
   Ефективність - співвідношення корисного результату і витрат. Якщо виробляють один продукт з одного ресурсу, то ефективність дорівнює відношенню випуску продукту до витрат ресурсу. Але для всієї економіки ефективність виміряти складно через різноманітність товарів, і крім того, суспільні блага
5. Короткий огляд фінансових криз
   Злети і падіння банківської активності, розширення і стиснення кредиту, біржові паніки і фінансові кризи відбувалися з вражаючою регулярністю. Існують численні свідчення банківських крахів і криз як розвинених, так і країнах, що розвиваються ринків. Фінансові кризи можна представити у вигляді
6. Короткі висновки
   Статистичні спостереження за функціонуванням національної економіки в часі показують тенденцію до зростання її результативності. Однак зростання відбувається не монотонно, а колебательно, виявляючи закономірну циклічність ринкової економіки. Пояснення цієї закономірності складає суть теорії
7. Короткі висновки
   Розподіл сучасної економічної теорії на два розділи - мікроекономіку і макроекономіку - грунтується на відмінності проблем, що становлять предмет вивчення кожної з них, і на використанні, поряд із загальними, специфічних методів дослідження. У мікроекономіці аналізують, як ринок
8. Короткі висновки
   Модель сукупного попиту та сукупної пропозиції дозволяє фактично об'єднати в єдине ціле такі різні погляди на економіку і проведення економічної політики, як неокласичний і кейнсіанський. Можливість зробити це пов'язана з тим, що в залежності від розглянутого періоду і передумов вигляд кривої