| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Кількісні обмеження на ринках впливають не тільки на споживання і трудову активність домашнього господарства, а й на його збереження. Якщо індивід очікує, що в майбутньому зустрінеться з раціонуванням на ринку праці, то він буде зберігати більше, ніж тоді, коли очікує зустрітися з обмеженням на ринку благ.
У мікроекономічному аналізі обсяг заощадження індивіда виводиться з максимізації його двухперіодне (многоперіодной) функції корисності U = U (C0y F0, Cv F,) -> max. З метою спрощення приймемо, що індивід працює тільки в нульовому періоді, а в наступному живе за рахунок майна і заощаджень нульового: З{ = (1 + i) (y0 - З0) - г П0. Заощадження здійснюються у вигляді попиту на реальні касові залишки: S = у0- З0 = М / Р. Тоді поведінку домашнього господарства в поточному періоді визначається максимізацією функції корисності U = U (C, (T-N), М / Р), де Т - календарне час; при бюджетному обмеженні PC + М = WN + П.
Включивши бюджетне обмеження в функцію корисності, отримаємо її величину з абсорбованим (поглинутим) бюджетним обмеженням:
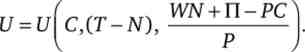
Хоча в явному вигляді обсяг заощаджень не представлений в числі аргументів функції корисності з абсорбованим бюджетним обмеженням, розмір заощаджень безпосередньо визначає її значення.
Графічно вид цієї функції представлений на рис. 13.2. Якщо при даних цінах індивіду вдається реалізувати гіпотетичні значення пропозиції праці, споживання і заощадження, то він витягує максимум корисності зі своєї господарської діяльності (точка Н).
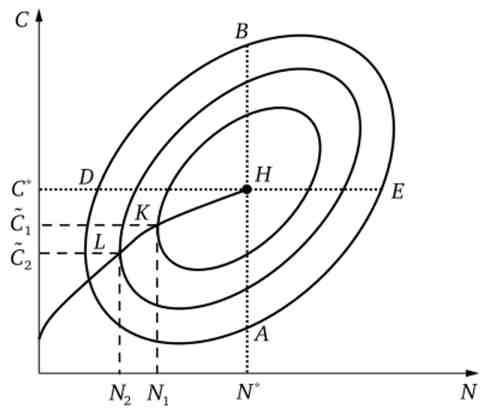
Мал. 13.2. Функція корисності з абсорбованим бюджетним обмеженням і нео- кейнсіанська функція споживання
Будь-яке відхилення від комбінації значень JV З супроводжується зниженням корисності. Чим далі поєднання N, С розташоване від точки Я, тим менше значення приймає функція корисності. Всі точки, що представляють однаково корисні для індивіда поєднання N і С, утворюють криву байдужості. Особливість кривих байдужості, що представляють функцію корисності з абсорбованим бюджетним обмеженням, полягає в тому, що вони утворюють еліпсоподібної лінії.
чому точка В представляє менший рівень добробуту, ніж точка Я? Адже при одній і тій же трудової активності індивіда в ситуації, представленої точкою споживання більше, ніж в ситуації, відповідної точці Я.
Це пояснюється тим, що в положенні, яка подається точкою В, заощадження індивіда малі в порівнянні з їх оптимальним розміром. У положенні, представленому точкою А, навпаки, заощадження надмірні. оскільки точки Aw В лежать на одній і тій же кривій байдужості, вони відповідають однаково корисним для індивіда ситуацій.
У ситуаціях, представлених точками D і Е, обсяги поточного споживання індивіда однакові, хоча точці Е відповідає більш тривала робота, ніж точці D. Тому точки DwE можуть перебувати на одній і тій же кривій байдужості лише за умови, що в ситуації, представленої точкою Е, обсяг заощаджень більше, ніж в точці D.
Оскільки аргументами функції корисності з абсорбованим бюджетним обмеженням є вектор цін і обсяг майна індивіда, то при зміні цих параметрів точка Я разом з усім сімейством кривих байдужості зміщується.
Простежимо за рис. 13.2 за поведінкою домашнього господарства при появі на ринку праці кількісних обмежень. Якщо індивід зможе продати тільки N{ одиниць праці, то його функція корисності досягне максимально можливого значення в ситуації, представленої точкою К. Ближчі до точки Я криві байдужості будуть йому недоступні. Отже, при раціонування на ринку праці па рівні Я, обсяг споживання індивіда складе Зг Якщо раціонування посилиться до Я2, то і споживання знизиться до С2, представленої точкою L. Поєднавши всі крапки на кривих байдужості, які обираються індивідом при різних рівнях раціонування на ринку праці, отримаємо графік залежності споживання індивіда від кількісного обмеження на ринку праці: З = С (а, Я), де а - вектор (Р, W, П), що визначає розташування точки Я.
Беручи до уваги, що кількісне обмеження на ринку праці визначає дохід індивіда у = у (Я), попит на блага раціонірованного на ринку праці домашнього господарства можна представити у вигляді неокейн- сіанской функції споживання: С = С (а, у). Вона відображає попит домашніх господарств на ринку благ при існуванні він став безробітним. При повній зайнятості споживання домашніх господарств характеризується неокласичної функцією споживання С = С (?).
Поведінка домашнього господарства на ринку праці в разі виникнення раціонування на ринку благ показано на рис. 13.3. У міру посилення раціонування на ринку благ з З Д ° Q? дійсне пропозицію праці знижується з Nx до Я2. Поєднавши всі крапки на кривих байдужості, відповідні максимальним значенням функції корисності при різних кількісні обмеження на ринку блага, отримаємо графік нео- кейнсіанської функції пропозиції праці Ns = NS(D, С).
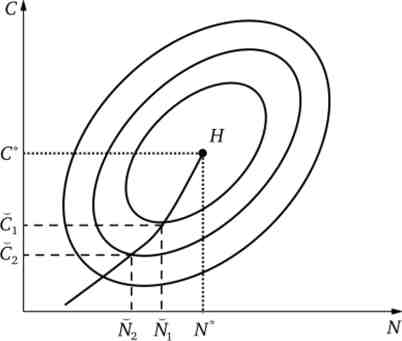
Мал. 13.3. Функція корисності з абсорбованим бюджетним обмеженням і нео- кейнсіанська функція пропозиції праці
Всі можливі варіанти поведінки домашнього господарства при виникненні раціонування на ринках праці або блага представлені на рис. 13.4 «клином», утвореним графіками неокейнсианских функцій споживання і пропозиції праці. Якщо ні па одному з ринків немає раціонування, то домашнє господарство реалізує ситуацію, представлену точкою Я. При рационировании на ринку праці буде реалізована ситуація, представлена точкою К. Коли раціонірован ринок благ, тоді поведінка індивіда представляє точка F.
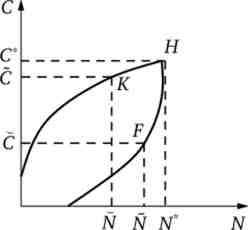
Мал. 13.4. Поведінковий «клин» домашнього господарства
На рис. 13.4 показана також одна з характерних особливостей поведінки домашнього господарства: якщо раціонування на ринках зросте на певну величину, то обсяг дійсного споживчого попиту або дійсного пропозиції праці скорочується на меншу величину (відрізок З * З більше відрізка N * N, а відрізок N * N більше відрізка З * С). Его пояснюється тим, що заощадження амортизують вплив кількісних обмежень на поведінку домашніх господарств: коли на ринку благ виникає раціонування, а на ринку праці його немає, тоді можна не скорочувати пропозицію праці, працюючи заради збільшення заощаджень.
приклад 13.1
Уподобання індивіда з бюджетним обмеженням: PC + М = UW + 10 представлені функцією корисності
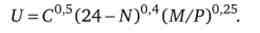
Виведемо неокласичні і неокейнсианские функції споживання та пропозиції праці цього індивіда. Відповідна завданню функ-ція Лагранжа має вигляд
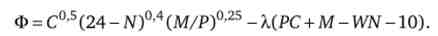
Вона досягає максимуму при
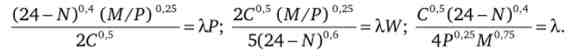
Звідси
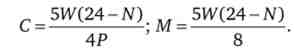
Підставивши ці значення в бюджетне рівняння, знайдемо гіпотетичні функції пропозиції праці, споживання благ і попиту на гроші домашнього господарства


Якщо індивіду не вдається продати більше N одиниць праці, то його бюджетне рівняння приймає наступний вигляд: РС + М = WN + 10, а функція Лагранжа ф = С0,5 (24 - N) 0,4 (М / Р) 0,25 - (РС + М- WN -10). В результаті ана-логічних наведеним вище розрахунків знайдемо

З формули (13.12) випливає, що в розглянутому прикладі при зменшенні раціонування на ринку купа на одиницю (при зростанні доходу індивіда на XV) номінальний попит на блага збільшиться на 2XV / 3.
Якщо індивіду не вдається купити більше З одиниць благ, то його бюджетне рівняння приймає наступний вигляд: РС + М = WN + 10, а функція Лагранжа -
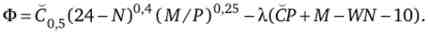
Тепер в результаті розрахунків отримаємо, що максимум корисності індивід отримує при

Для побудови поведінкового «клину» приймемо, що XV = 1; Р = 2. Тоді за формулами (13.9) і (13.10) знайдемо координати вершини поведінкового «клину»: Ny = 12,17; З * = 7,39, а за формулами (13.12) і (13.13) - кейнсіанські функції споживання та пропозиції праці

Їх графіки зображені на рис. 13.5.
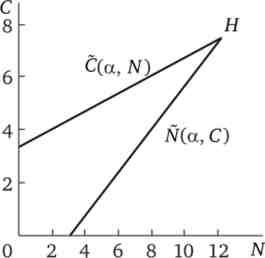
Мал. 13.5. Поведінковий «клин» (приклад)
Звернемо увагу на те, що розташування вершини поведінкового «клину» визначається вектором цін. Щоб визначити, який з них забезпечує загальне економічне рівновагу по Вальрасу, потрібно в модель включити підприємницький сектор.