Рівняння Слуцького для ринку праці

У точці оптимуму на ринку праці індивід орієнтується на одне і те ж кількість роботи - будь то Маршалліанская функція пропозиції праці або функція компенсованого пропозиції праці:

Знайдемо динаміку компенсованого пропозиції праці під дією зміни заробітної плати

dl_

dw

• 81 i
• ---L або

dE

т ттт ^де т ^{д 1}"

Так як по лемі Шепарда: - = -1, то: -

dw dw

Це і є рівняння Слуцького для ринку праці.

51^м dL^H

Тут - загальний ефект ціни (ефект заробітної плати); -> 0 -

dw qjm dw

ефект заміни для пропозиції праці; -<0 - ефект доходу для пропозиції праці. ^

Завдання, що ілюструє теорію

Вивести функцію пропозиції праці для індивіда з корисністю: 1 / (С, R) = JC R при бюджетному обмеженні: C = vv L + /₀ і тимчасове обмеження: R = l-L. Знайти непряму функцію корисності. Дослідити дану функцію пропозиції праці на ефект заміни і ефект доходу. Перевірити, чи виконується рівняння Слуцького. Що станеться з індивідуальним пропозицією праці, якщо держава надасть даному споживачеві акордних субсидію в розмірі 4 дол.? Яким чином зміниться пропозиція праці, якщо замість акордною субсидії держава запропонує такий варіант

субсидії: S = 4 - ^^?

Введемо основні позначення: U - корисність; З - товарний набір; R - вільний час індивіда; L - час роботи; /₀ - нетрудовий дохід (відсотки з рахунку в банку, спадок і т. д.).

Так як раціональність споживача є базовим припущенням в мікроекономіці, то він буде діяти таким чином, щоб кожна додаткова одиниця грошей, витрачена на благо, принесла б однакову корисність. Цей принцип рівноваги в споживанні також називають еквімаржіналь- ним принципом. Таким чином, в точці оптимуму буде справедливо рівність

де MU_C - гранична корисність товарного набору С; MU_R - гранична корисність вільного часу; Р - ціна товарного набору С; iv - ставка заробітної плати.

Форма бюджетного обмеження говорить про те, що ціна товару дорівнює одиниці. Але ми можемо спочатку розглянути більш загальний випадок, коли Р - деякий довільне число. При необхідності можна підставити Р = 1 і отримати модель, яка буде більш простий.

Обчислимо граничні корисності і знайдемо оптимальне співвідношення вільного часу і кількості придбаних товарів

Підставивши в це співвідношення формули: C = w-L + I₀ і R = l-L ми зможемо вивести функцію пропозиції праці

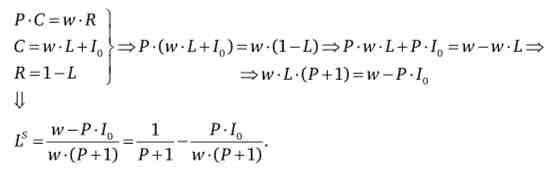
Далі знайдемо оптимальні значення вільного часу і товарного набору і виведемо на підставі отриманих значень непряму функцію корисності

Проілюструємо це графічно:

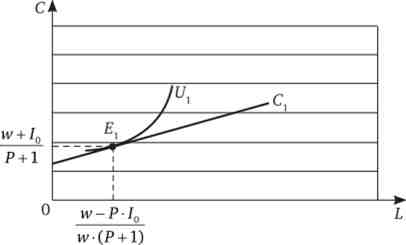
Для того щоб дослідити функцію пропозиції на ефекти заміни і доходу, необхідно подивитися, як будуть змінюватися оптимальні значення С і L при зміні бюджетного обмеження. Припустимо, що змінюється ставка заробітної плати в а раз. Тобто iv₂ = Mv. Розглянемо випадок, коли а > 1, заробітна плата збільшилася. Отримаємо нову функцію корисності і новий оптимум

Проілюструємо це графічно:

Знайдемо ефекти заміни і доходу по Слуцькому, т. Е. За умови, що споживачеві буде доступний старий набір при новій ставці заробітної плати

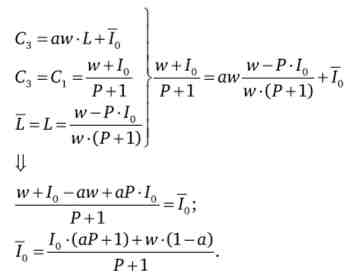
(AP + l) + w- (l-a)

Отримуємо, що: C₃= Aw L + --- -.

Знайдемо оптимум методом Лагранжа в разі максимізації функції корисності U = VC R = VC (l-L) за умови, що

Проілюструємо для наочності із зазначенням ефектів:

Ефект заміни дорівнює Ефект доходу становить

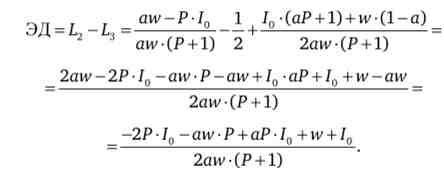
Ефект ціни дорівнює

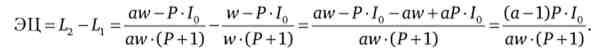
Для більш точного визначення ефектів необхідно задати параметр а. Можна виділити три випадки (заробітна плата зростає, не змінюється або знижується):

Перевіримо тепер, чи виконується рівняння Слуцького:

Тотожність є вірним, отже, рівняння Слуцького виконується. Якщо держава надасть даному споживачеві акордних субсидію в розмірі 4 дол., То крива бюджетного обмеження зрушить вгору на 4 дол.

Тобто: C_sllbl= C + 4 = w-L + I₀+4.

Знайдемо нову пропозицію праці з умови максимізації корисності при новому бюджетному обмеженні

У загальному випадку

При введенні акордною субсидії пропозицію праці зміниться наступним чином:

Пропозиція праці знизиться на величину ---.

w-PI₀

Це можна продемонструвати графічно:

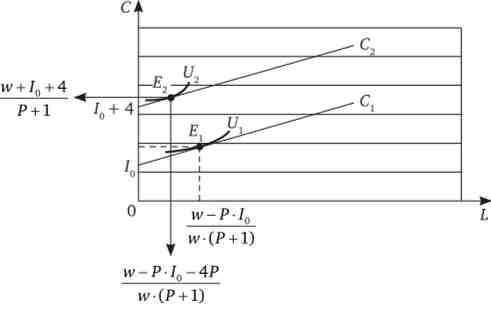
Якщо ж держава пропонує субсидію у вигляді: S ⁼ 4^-~~> щось нове бюджетне обмеження набуде вигляду

тоді

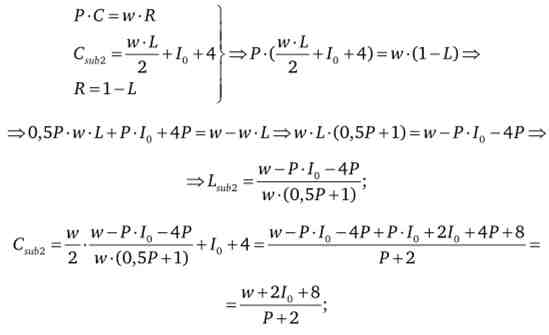
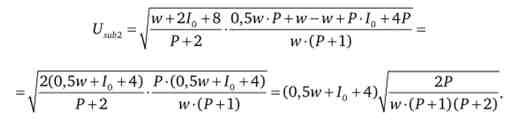
При цьому пропозиція праці зміниться:

"(Iv-P /₀-4P) (P + l),

Нова пропозиція праці складе: ---=?.

(0,5P + l) (w-P /_o)

1. Види виробничих функцій
   У виробництві можуть застосовуватися різні ресурси, які по-різному співвідносяться між собою. Ступінь впливу ресурсів друг на друга при незмінному випуску визначає вид виробничих функцій. Класифікація видів виробничих функцій багато в чому нагадує класифікацію видів переваг споживача. І це
2. Види рівноваги
   По-перше, чи є рівновага стабільним? Рівновага - це всього лише певна тенденція ринку. Що станеться, якщо в силу випадкових факторів ціна виявиться вище або нижче рівноважної? Чи прийде ринок сам до первісного рівноваги або коливання ринкових цін будуть тривати нескінченно довго, так ніколи
3. Вибір споживача в умовах невизначеності і ризику, опис невизначеності та ризику
   «Розділяй і володарюй» - мудре правило; але «об'єднуй і направляй» - ще краще. Йоганн Вольфганг Гете, німецький поет Після вивчення цього розділу студенти будуть: знати особливості вибору споживача в умовах невизначеності і ризику; вміти виявляти типи індивідів по їх відношенню до ризику;
4. Умови внутрішнього і кутового оптимумів
   Оптимальну поведінку споживача означає, що він прагне витратити свої гроші найбільш ефективно, т. Е. Так, щоб корисність вибраного набору виявилася максимальною. Однак це не означає, що споживач завжди буде купувати обидва товари (або всі можливі продукти товарного світу). Ми можемо говорити
5. Цінова дискримінація першого ступеня
   Фірма в ідеалі хотіла б продавати кожну одиницю товару тому споживачеві, який оцінює її найвищим чином. Тоді перша одиниця товару продавалася б по найбільшій ціні самому нетерплячому споживачеві. Друга одиниця товару могла б бути проданою за нижчою ціною. Потім ціна знижувалася і знижувалася
6. Точкова і дугова еластичність
   для того щоб знайти величину цінової еластичності попиту, можна використовувати дві формули. Якщо мова йде про оцінку еластичності в точці, т. Е. При невеликих змінах ціни, скажімо, в околиці рівноважної ціни, застосовується формула точкової еластичності: де Q 1 - первісна величина попиту
7. Теорема Коуза
   При наявності можливості переговорів між зацікавленими сторонами, залученими в процес створення зовнішніх ефектів, причому ці переговори не тягнуть за собою значних трансакційних витрат, механізм добровільних угод гарантує оптимальний розподіл ресурсів. Якщо відсутній ефект доходу, пов'язаний
8. Стимули до вертикальних контрактами
   Крім мотивів, які лежать в основі прагнення фірми до вертикальної інтеграції, для використання вертикальних обмежувальних контрактів вступають в дію додаткові стимули. Проблема «безбілетника» серед дилерів (торговців ). У тих випадках коли один виробник товару поширює свою продукцію серед