| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
У виробництві можуть застосовуватися різні ресурси, які по-різному співвідносяться між собою. Ступінь впливу ресурсів друг на друга при незмінному випуску визначає вид виробничих функцій.
Класифікація видів виробничих функцій багато в чому нагадує класифікацію видів переваг споживача. І це не дивно, так як теорія виробництва і теорія споживання розвивалися паралельно і значно доповнювали один одного по інструментах аналізу.
Стандартна виробнича функція. Найбільш популярною в мікроекономічному аналізі виробничої функцією є функція Кобба - Дугласа: Q = К "1р. Для цієї функції ресурси - праця і капітал - можуть заміняти один одного, але в певних пропорціях. В даному випадку виконуються всі аксіоми виробничого вибору. Ізокванти представлені на рис. 11.3.
Приклади виробництв, які можуть бути охарактеризовані функцією Кобба - Дугласа, підібрати досить складно. Проте наведемо деякі з них: економіка в цілому (хоча це вже рівень макроаналізу); копіювальний апарат і менеджер по роботі з клієнтами на фірмі; персонал і обладнання; борошно для виробництва тортів і виготовляє їх кондитер. Деякі види виробництва, такі, як виготовлення одягу, взуття, предметів гігієни, продуктів харчування, теж можна оцінити як функцію Кобба - Дугласа.
Виробнича функція Леонтьєва. Для деяких виробництв заміна одного ресурсу іншим неможлива з технологічних причин. Для того щоб товар був прознавств, ресурси повинні застосовуватися тільки разом, в певних пропорціях. Наприклад, виготовлення шафи для одягу вимагає одного працівника (теслі) і три-чотири дошки. Тут ресурси будуть взаємодоповнюючими. Така виробнича функція теж має своє «власне ім'я». Вона називається виробничою функцією Леонтьєва (в честь американського економіста російського походження) і виглядає наступним чином: Q = min {a.K; (31), де аїр - позитивні константи, що характеризують технологію виробництва (рис. 11.4). Знак min - знак мінімуму - показує, що з усіх наявних обсягів ресурсів необхідно взяти тільки певну пропорцію. Якщо будь-якого фактора є в наявності більше, ніж це зазначено в цій пропорції, додаткові обсяги ресурсу виявляться зайвими.
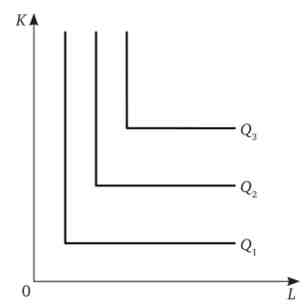
Мал. 11.4. Виробнича функція Леонтьєва Історична довідка
Василь Леонтьєв (1906-1999), американський економіст, лауреат Нобелівської премії з економіки 1973 р У 1925 р закінчив Ленін-Градський університет, викладав на кафедрі економічної географії. Проходив стажування в Німеччині. Працював економічним радником уряду Китаю в Нанкіні, потім в Інституті світової господарства. З 1931 р переїхав в США. Став професором Гарвардського університету. Очолював створений ним Гарвардський проект економічних досліджень. У 1970 р був обраний президентом Американської економічної асоціації. З 1975 року працював в Нью-Йоркському університеті, був директором Інституту економічного аналізу при цьому університеті. Керував роботами по прогнозуванню світового економічного розвитку. Головне досягнення - розробка теоретичних основ методу «витрати-випуск».
Як приклади виробництв, описуваних даної виробничої функцією, можна навести такі:
Взаємна доповнюваність може характеризувати не тільки праця і капітал, а й різні види капіталу або різні види праці. Наприклад, взаємодоповнюючими ресурсами будуть: системний блок комп'ютера і «миша»; бізнес-інкубатор і інфраструктура; електрику і верстат з ЧПУ; машина і бензин; бухгалтер і юрист на фірмі; керівник і секретар; працівники відділу продажів і фахівці з інформаційних технологій.
Лінійна виробнича функція. В інших випадках ресурси можуть легко замінювати один одного. Ми можемо писати олівцем і ручкою, робити фотографії звичайним і цифровим фотоапаратом, готувати обід на електричній і газовій плиті. У всіх цих випадках фактори виробництва виявляться взаємозамінними. Виробнича функція, відповідна таким видам діяльності, називається лінійної. Оскільки заменяемость необов'язково повинна бути в співвідношенні 1: 1, обсяги ресурсів, що входять в лінійну виробничу функцію, мають коефіцієнти: Q = alC + | 3L (рис. 11.5).
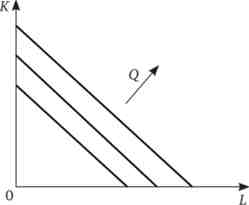
Мал. 11.5. Лінійна виробнича функція
Приклади даного виду виробничої функції - це:
Виробництво з нейтральним ресурсом. Іноді один з ресурсів виявляється зайвим для процесу виробництва. Наприклад, при наявності екскаватора працівник з лопатою буде не потрібен. Канаву може вирити техніка. Тут працівник - непотрібний ресурс. Він називається ще нейтральним ресурсом, т. Е. Це такий ресурс, який не робить впливу на випуск (нейтральний до випуску). Тоді виробнича функція буде залежати тільки від обсягів потрібного ресурсу - або капіталу: Q = осК, або праці: Q = pi (рис. 11.6).

Мал. 11.6. Виробництво з нейтральним ресурсом
Практично в будь-якій сфері діяльності нам можуть зустрітися нейтральні ресурси: використаний папір; рахунки при наявності комп'ютера та (або) касового апарату; стаціонарний телефон при наявності мобільного і т. д.
Виробництво і антіресурс. Бувають випадки, коли ресурси несприятливо впливають безпосередньо на процес виробництва. Такий фактор називається антіресурсом. Їм можуть бути комп'ютерний вірус, радіоперешкоди, несприятливі погодні умови. Звичайно, фірма не прагне придбати антіресурс. Скоріше, мова йде про побічні результати виробництва або неврахованих чинниках. Наявність антіресурса видозмінює виробничу функцію: Q = aL- (SK + А, де капітал виступає у вигляді антіресура, збільшення якого веде до зниження випуску (тут Л - якась постійна величина) (рис. 11.7).
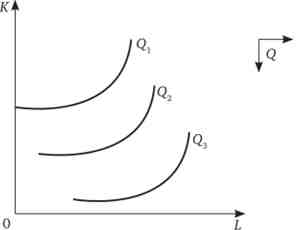
Мал. 11.7. Виробництво, де зустрічається антіресурс
Антіресурси оточують фірму в дуже багатьох випадках. Доста-точно згадати такі ситуації, як:
Виробництво і несумісні ресурси. У деяких випадках ресурси можуть шкідливо діяти один на одного і потім вже на випуск. Такі ресурси характеризуються як несумісні. Подібна ситуація може зустрічатися в хімічному виробництві, де різні інгредієнти можуть вступати в хімічну реакцію один з одним і тим самим чинити негативний вплив на випуск в цілому. Виробництво можливо тільки при ефективному використанні одного з ресурсів.
Припустимо, підприємство випускає оліфу. Але при виробництві її на верстатах виділяються шкідливі для людського організму речовини (пов'язано з температурою), чого не відбувається при змішуванні фарби вручну. Таким чином, ми повинні використовувати або тільки верстати, або тільки людська праця для виробництва оліфи.
Виробнича функція приймає наступний вигляд: Q = (АК)2 + ф!)2 (Рис. 11.8).
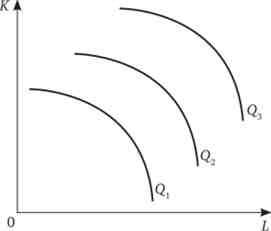
Мал. 11.8. Виробництво при несумісних ресурсах
Прикладами несумісних ресурсів можуть служити:
Завдання фірми полягає зазвичай в тому, щоб виявити несумісні ресурси, ізолювати їх і використовувати не в одному, а в різних виробничих процесах.
Квазілінійну виробнича функція. Окремо виділяють квазілінійну виробничу функцію: Q = У (Аю + р ?, в якій один з факторів змінюється лінійно (в нашому випадку праця), а інший нелінійно (капітал) (рис. 11.9). Ми бачимо, що для цього виробництва випуск залежить головним чином від обсягу нелінійного ресурсу. Навіть якщо лінійно змінюється ресурс відсутній (L = 0), товар буде прознавств. Як правило, це характерно для виробництв з великими обсягами капіталу (капіталомістких виробництв): випуск турбін, літаків, автомобілів, де є жорсткий конвеєр (нелінійний ресурс), до торий можуть обслуговувати трохи більше або трохи менше число працівників. Невеликі коливання чисельності зайнятих на конвеєрі не вплинуть на випуск, в той час як додаток або скорочення конвеєрної лінії відразу ж змінить обсяг виробленої продукції.
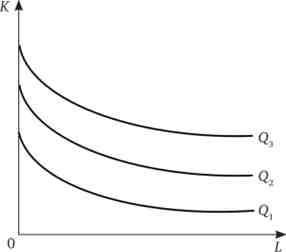
Мал. 11.9. Квазілінійну виробнича функція
Іншими прикладами квазилинейной виробничої функції можуть служити:
Ламана ізокванта. Часто буває так, що технологія передбачає
використання лише декількох допустимих методів виробництва. В цьому випадку не все набори ресурсів виявляються в технологічній галузі виробництва фірми. Можливості переходу від однієї допустимої технології до іншої зображуються за допомогою ламаної ізокванти (рис. 11.10).
На рис. 11.10 показана ситуація, коли у фірми є чотири технології виробництва. Промені Р, Р2, Р3, Р4, виходять з початку координат, характеризують допустимі технології випуску. Обсяги Q, Q2, Q3 дані як приклади різного рівня випуску (на графіку випуск зростає в напрямку від Q3 до Qj). Наприклад, якщо ми візьмемо залізо і вуглець, то в одному випадку виходить м'яка сталь, в іншому - тверда сталь, а в третьому - чавун.
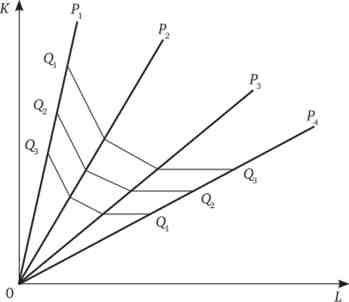
Мал. 11.10. ламана ізокванта
У загальному вигляді виробнича функції даного типу може бути представлена як відповідні діапазони зміни випуску, наприклад, таким чином:
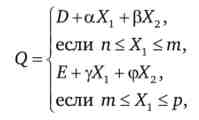
де Xj і Х2 - різні фактори виробництва.
Зауважимо, якщо число допустимих технологій зростає, зламів стає все більше і більше. У граничному випадку ламана ізокванта наближається до гладкою формі функції Кобба - Дугласа. Це дуже важливий висновок. На думку інженерів, ламана ізокванта найбільш реалістично представляє виробничі можливості сучасних галузей промисловості. А раз функція Кобба - Дугласа є її нескінченним наближенням, то аналіз даної функції буде ефективним моделюванням процесів реального виробництва.
Виробнича функція CES. Виробнича функція з постійною еластичністю заміщення факторів виробництва (Constant elasticity substitution - CES) Є узагальненням виробничих функцій Кобба - Дугласа, Леонтьєва та лінійної. Її формула має вигляд
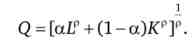
У такий функції ст = 1 / (1 - р), т. Е. Еластичність заміщення постійна, але не обов'язково дорівнює одиниці. Виробничі функції Кобба - Дугласа і Леонтьєва є окремими випадками функції CES: якщо р - »0, то ст -" 1, а якщо р - »оо, то ст -> 0.
Виробництво з дискретним ресурсом. Якщо один або обидва ресурси можуть бути використані тільки в цілих кількостях (наприклад, в штуках або кількості людей), то ізокванти не можуть виглядати як безперервні лінії. Рівні однакового випуску виявляться точками (рис. 11.11).
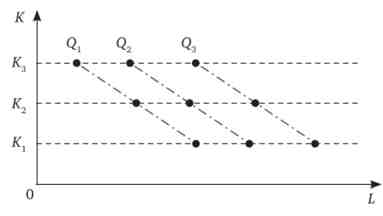
Мал. 11.11. Ізокванти для виробничої функції з дискретними ресурсами
Точка ефективного випуску. Якщо ми хочемо відобразити наявність у виробництві мінімальної комбінації ресурсів, яка допускає ефективний випуск, то тоді нам знадобиться відповідна виробнича функція виду
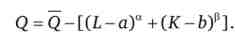
Ця виробнича функція визначає структурну одиницю МЕР (рис. 11.12). При недостатньому обсязі ресурсів дана залежність може приймати вид виробничої функції Кобба - Дугласа. Якщо один з ресурсів в надлишку, то цей фактор виробництва стає антіресурсом. Зайві його обсяги не ведуть до зростання випуску.
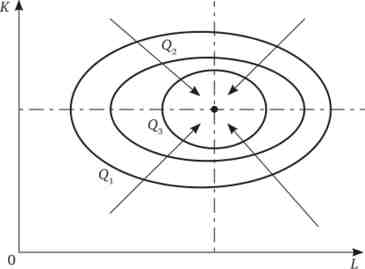
Мал. 11.12. Виробництво з точкою ефективного випуску