| Головна |
| « Попередня | ЗМІСТ |
|---|
Розглянемо тепер дещо іншу задачу оптимізації:
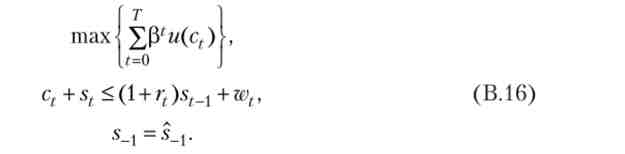
тут функція і така ж, як і в параграфі В.1, а горизонт планування Тзнову ж таки може бути як кінцевим, так і нескінченним (7 '= °°). Таке завдання інтерпретується як вибір репрезентативного споживача між споживанням і заощадженнями. Кожен період часу дохід агента, який він вважає заданим, складається із заробітної плати wt і відсотків від інвестованих заощаджень за ставкою rv
Зауважимо, що з причин, викладених у параграфі В.1, ми відразу ж не вказуємо в якості умов завдання неотрицательность споживання в кожному періоді, з,> 0. У той же час ми не накладаємо і умови невід'ємності заощаджень s,> 0. Однак якщо допустити можливість необмежено брати в борг (s,<0), то рішення, що цікавить нас завдання не існуватиме. Очевидно, агент має можливість займати і споживати будь-яку кількість продукту, яке він тільки захоче, виплачуючи відсотки по боргу шляхом нових, ще більших позик в наступних періодах. Така поведінка називається схемою Понці (будівництвом фінансової піраміди). В цьому випадку бюджетне обмеження ct +st <(l + ?}) St_1 + wt фактично не є обмеженням. Тому до задачі (В. 16) необхідно додати обмеження па позики, щоб виключити можливість фінансових пірамід. Такого роду умови називаються умовами No-Ponzi Game. Ми розглянемо їх походження для випадку як кінцевої, гак і нескінченної траєкторії.
послідовність (C *t, s *t) J= (), яка задовольняє завданню (В.16) з накладеним умовою No-Ponzi Game, ми будемо називати рішенням завдання споживача.
Кінцевий горизонт планування
Розглянемо задачу (В.16) на кінцевому горизонті планування. умовою No-Ponzi Game в даному випадку зазвичай є вимога, щоб в кінці періоду планування борг споживача не був позитивним. Оскільки борг, накопичений до моменту часу Т, являє собою величину - лу, то вимога полягає в тому, щоб лу> 0. Однак зручніше розглядати не саму величину боргу, а борг, назнавств до початкового моменту часу. Тому умова No-Ponzi Game для завдання з кінцевим горизонтом планування можна записати так:
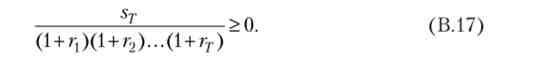
Таким чином, завдання споживача виглядає наступним чином:
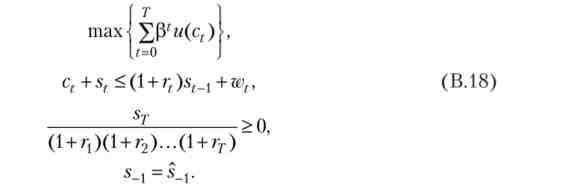
Зауважимо тепер, що завдання споживача (В. 18) можна переписати в більш зручному вигляді, перетворивши всі бюджетні обмеження і умова No-Ponzi Game в міжчасового бюджетне обмеження. Для цього розглянемо бюджетне обмеження в останньому періоді Т. Висловимо з нього величину sr_j, і підставимо її в попереднє бюджетне обмеження
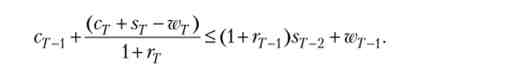
Поступаючи тепер так само з величиною sT_2 і продовжуючи цей процес до бюджетного обмеження початкового періоду, ми отримаємо
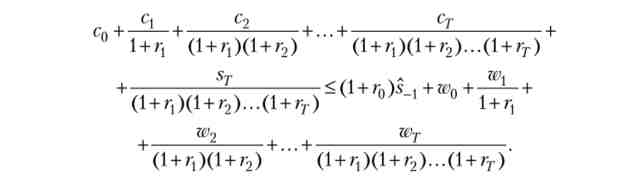
З огляду на тепер умова No-Ponzi Game, ми приходимо до єдиного обмеження
Це нерівність означає, що поточна потік споживання репрезентативного агента в усі моменти часу (признавств до початкового моменту) не повинен перевищувати його сукупного доходу (теж приведеного до початкового моменту часу). Дохід цей складається з початкових заощаджень і потоку заробітних плат. Оскільки дохід споживача вважається екзогенно заданим, в правій частині міжчасового бюджетного обмеження стоїть якась постійна величина. Позначимо її через I. Тоді задача, яку вирішує споживач, перепишеться так:
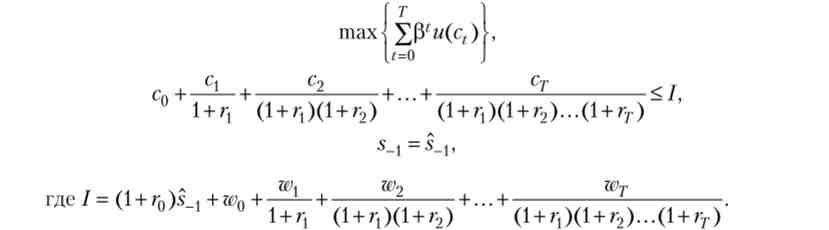
Необхідні і достатні умови для вирішення такого завдання, еквівалентної вихідної, можна отримати, скориставшись теоремою Куна - Таккера. Нехай А.- множник Лагранжа для міжчасового бюджетного обмеження. Тоді функція Лагранжа має вигляд
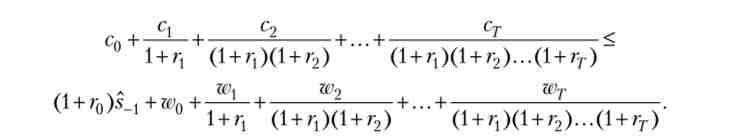
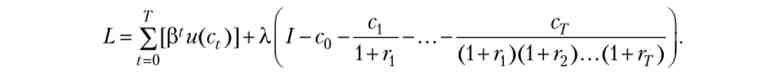
Умови першого порядку і умови доповнює нежорсткості записуються як
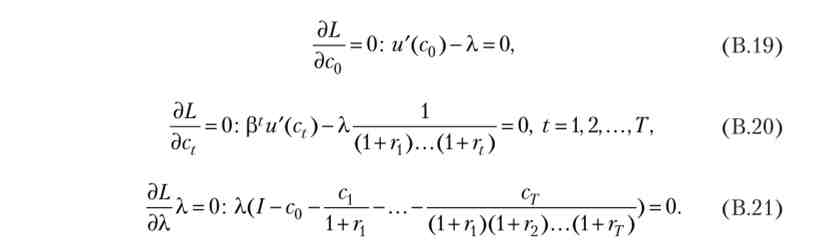
З (В.19) відразу ж випливає, що А0, а тоді бюджетне обмеження виконується як рівність:
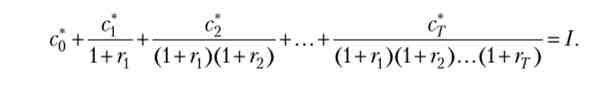
Умова (В.22) дуже схоже на умову (В.8) для конечномерной оптимальної завдання, і, як ми зараз побачимо, теж є прототипом умови трансверсальності для завдання споживача на нескінченному обрії. З (В.22) випливає, що sf = 0, т. Е. В термінальний момент часу зберігати неоптимально.
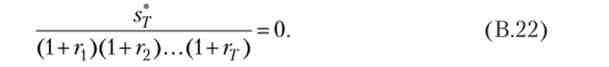
Крім того, раз міжчасового бюджетне обмеження виконується як рівність, то і всі бюджетні обмеження у вихідній задачі виконуються як рівності
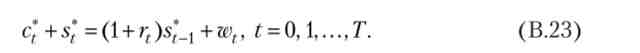
Нарешті, комбінуючи умови (В. 19) - (В.20) в сусідні моменти часу, і позбавляючись від множника Лагранжа X, ми знову отримуємо умови першого порядку (рівняння Ейлера)
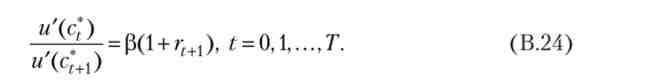
Таким чином, ми приходимо до наступного твердження.
Затвердження В.2. Послідовність (з *, s *t) j= 0 при заданому початковому значенні s_x = s_x є рішенням задачі (В.18) на кінцевому горизонті тоді і тільки тоді, коли виконуються умови {В.22) - (В.24).
Нескінченний горизонт планування
Розглянемо тепер задачу (В. 16) на нескінченному обрії планування. У цьому випадку умова No-Ponzi Game є узагальненням умови (В. 17) і має вигляд
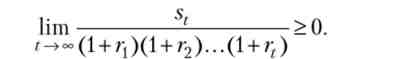
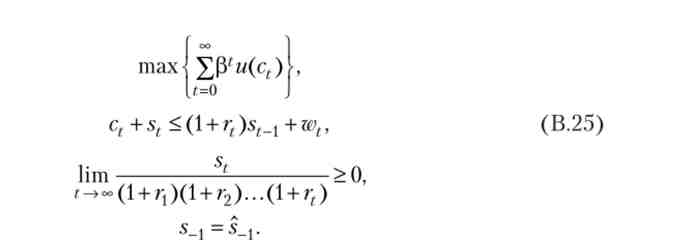
змістовно це вимога означає, що в межі весь борг споживача повинен бути виплачений. Таким чином, завдання споживача має вигляд
Аналогічно нагоди кінцевого горизонту планування, обмеження в задачі (В.25) можна переписати через міжчасового бюджетне обмеження. Висловлюючи з бюджетного обмеження для довільного моменту t величину st_j, підставляючи її в попереднє бюджетне обмеження, а потім продовжуючи цей процес з s, _2, ...,% ми отримуємо
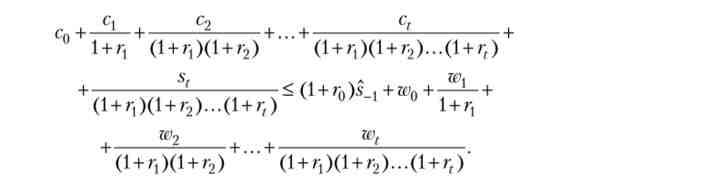
Переходячи в цій формулі до межі t-> °° і враховуючи умову No-Ponzi Game, ми отримуємо міжчасового бюджетне обмеження на нескінченному обрії
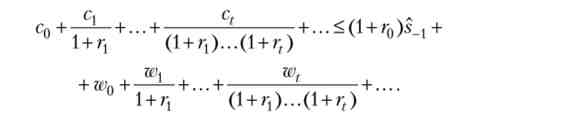
Позначаючи знову праву частину (дохід на всьому нескінченному обрії) цього обмеження через I, а відповідний множник Лагранжа через X, можна записати функцію Лагранжа як
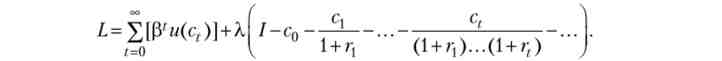
Умови першого порядку і умови доповнює нежорсткості записуються як
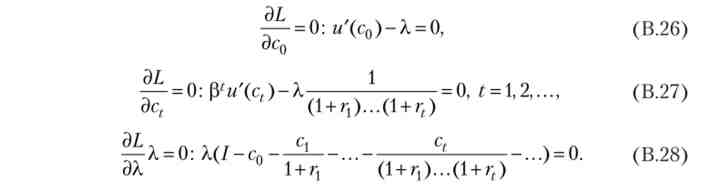
З (В.26) відразу ж слід, що X0, і що міжчасового бюджетне обмеження виконується як рівність. Це відповідає тому, що рішення задачі споживача характеризується наступним рівністю:
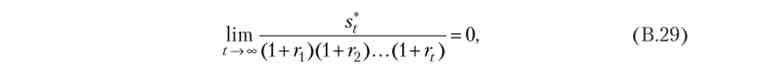
яке називається умовою трансверсальності.
Підкреслимо важлива відмінність між умовою No-Ponzi Game і умовою трансверсальності. Перше є властивість самого завдання, а друге - характеристика оптимального рішення. Умова No-Ponzi Game означає, що заощадження агента в межі не повинні бути негативними. Умова ж трансверсальності, навпаки, забороняє заощаджень агента бути занадто великими.
Як і в скінченномірному випадку, бюджетні обмеження в усі моменти часу будуть виконуватися як рівності
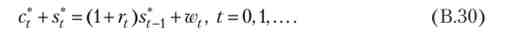
Нарешті, умови теореми Куна - Таккера (В.26) - (В.27) дають нам вже знайомі умови першого порядку, які виконуються в усі моменти часу:
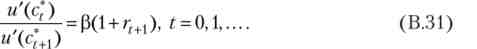
Речення В 2. Послідовність (ct, s]) " 0 при заданому початковому значенні .v_, = Є рішенням задачі {В.25) на кінцевому горизонті тоді і тільки тоді, коли виконуються умови (В.29) - (В.31).