| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Розглянемо наступну задачу оптимізації:
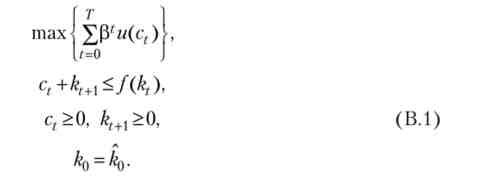
тут 0 <(3< 1, обмеження повинні виконуватися в усі моменти часу t = 0,1, ... Т, а горизонт планування Тможе бути як кінцевим, так і нескінченним (Г °°). Щодо функцій м: М+-> Кі /: М+ -> М+ будемо припускати, що вони:
Крім того, за замовчуванням вважається, що / (0) = 0. Фактично, саме це завдання зазвичай фігурує в моделі Рамсея. Часто її ще називають проблемою оптимального зростання або проблемою центрального планувальника. Під час обговорення цього завдання зручно апелювати до її економічним змістом. Тому ми будемо інтерпретувати і як функцію корисності, / як виробничу функцію, величину ct як споживання, а?(+1 як запас капіталу в момент часу? + 1. У цьому випадку нерівності с, + kl + i < f {k,) являють собою бюджетні обмеження: не можна спожити і запасти більше (єдиного) продукту, ніж вироблено. Вирішення цього завдання, послідовність (з ', / е, *+] ) j= 0, ми будемо називати оптимальної траєкторією.
Кінцевий горизонт планування
Розглянемо задачу (В.1) на кінцевому горизонті планування. Формально, при зроблених припущеннях, вона являє собою конечномерного завдання опуклого програмування. Необхідні і достатні умови для її вирішення виводяться з теореми Куна - Таккера, і основну роль в цих умовах грають двоїсті оцінки обмежень (множники Лагранжа / Куна - Таккера).
Зауважимо, однак, що перед застосуванням цієї теореми ми можемо виявити деякі властивості рішення і тим самим спростити вихідну задачу. Так, в силу того що корисність від споживання і строго зростає, на оптимальній траєкторії всі бюджетні обмеження будуть виконуватися як рівності. Справді, якщо з? + Й?+1 ct не може бути оптимальним.
Крім того, з умов Инада для функції корисності (lim г //(С) = + °°) випливає, що ct = 0 ніколи не може оить оптимальним, так що на оптимальної траєкторії завжди з *> 0. Тим самим умови невід'ємності зг0 можна ігнорувати при вирішенні. Ми свідомо знаємо, що вони не будуть зв'язують (англ, not binding), А відповідні їм множники Лагранжа дорівнюватимуть нулю.
Тепер, пам'ятаючи про те, що / (0) = 0, неважко бачити, що / е *+1 > 0, t = 0,1, ..., Т - 1. Якби в якийсь момент виявилося, що запас капіталу дорівнює нулю k *t = 0, то в наступному періоді виробництво в економіці зупиниться, і, отже, з,+1 = 0. А це, як ми вже переконалися, неоптимально. Таким чином, множники Лагранжа, що відповідають умовам &,+10 для? = 0,1, ..., Г-1, теж дорівнюють нулю. Однак, і це дуже важливо, ми не можемо ігнорувати умова невід'ємності kp+1 > 0, так як для нього подібна логіка вже не працює.
Введемо тепер множники Лагранжа qt, t = 0,1, ..., Г для Т бюджетних обмежень ct +^+1 < нехай рт - множник Лагранжа для залишається обмеження kp+i > 0. Функція Лагранжа (лагранжіан) для нашої задачі має наступний вигляд:
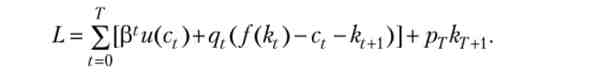
Умови Куна - Таккера записуються наступним чином:
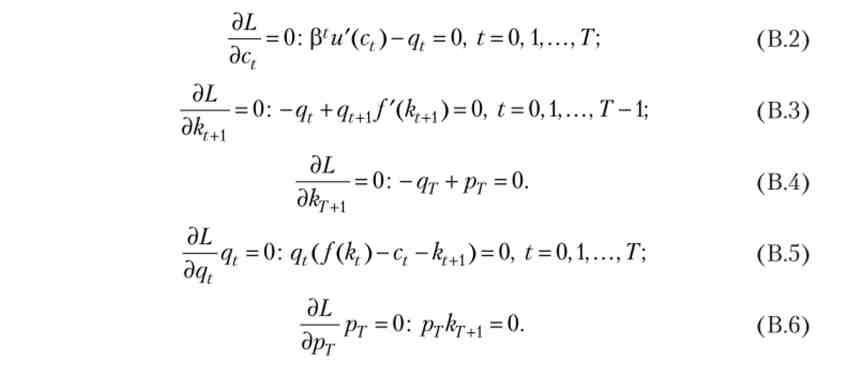
Перші три умови є умови стаціонарності (умови першого порядку). Останні дві умови відомі як умови доповнює нежорсткості. Нагадаємо, що вони означають наступне: якщо множник Лагранжа позитивний (наприклад, qt > 0), то відповідне обмеження є сполучною (англ, binding), Т. Е. Виконується як рівність, f (kt) -ct -kt + x = 0. Якщо ж обмеження виконано як суворе нерівність, то відповідний множник Лагранжа дорівнює нулю.
Помітивши тепер, що ис) > 0 Vc, з (В.2) ми знову отримуємо qt > 0, а значить, з (В.5) випливає, що бюджетні обмеження на оптимальної траєкторії дійсно виконуються як рівності:
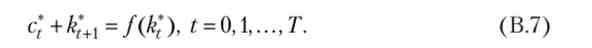
Тоді з (В. З) слід, що рт > 0, і умова доповнює нежорсткості (В.6) означає, що

Споживач нічого не запасає в самий останній період, оскільки він вже не зможе отримати від цього ніякої користі. Для нього оптимально в останньому періоді свого життя спожити все, що було вироблено. Така умова в конечномерной завданню здається тривіальним, але даний висновок виявиться корисним при формулюванні аналога цієї умови в нескінченновимірної задачі (так званого умови трансверсальності).
З умови (В. З) ми отримуємо, що
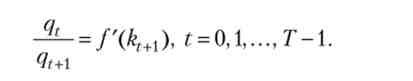
А записуючи умови (В.2) для двох сусідніх моментів часу і ділячи одне з них на інше, отримаємо
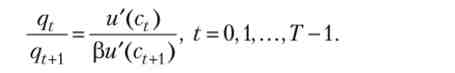
Таким чином, виключаючи множники Лагранжа, ми приходимо до набору
співвідношенні
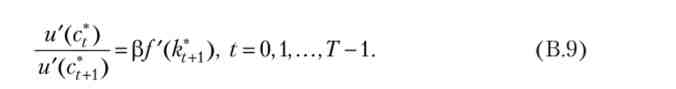
Умова типу (В.9) в оптимізаційних задачах, фактично є умовою першого порядку і зв'язує два послідовних значення змінної управління, називається рівнянням Ейлера. Щоб прояснити економічний сенс рівняння Ейлера, перепишемо його у вигляді
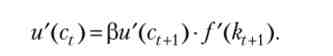
У лівій частині варто гранична корисність від споживання одиниці продукту сьогодні. У правій же частині варто гранична корисність від споживання завтра того, що можна було б сьогодні зберегти - множник $ U '(ctM) показує збільшення корисності в наступному періоді, a f '(kt +1) являє собою «дохідність» збереженості одиниці продукту (на скільки одиниць може вирости споживання в наступному періоді завдяки виробництву). Таким чином, рівняння Ейлера можна інтерпретувати як рівність граничних витрат і граничних вигод від заощадження одиниці продукту між двома сусідніми моментами часу.
Справедливий наступний результат (фактично, теорема Куна - Так-кер для завдання (В.1) з кінцевим горизонтом планування).
Затвердження В.1. Послідовність (з *п k *tMj [10 при заданому початковому значенні k0 = kd є рішенням задачі (В.1) на кінцевому горизонті тоді і тільки тоді, коли виконуються умови (Б.7) - (В.9).
Послідовність (з *, k *t + {) J= 0 містить 2Г + 2 невідомих, і умови (Б.7) - (В.9) представляють собою в точності 2Т + 2уравненій. Їх можна записати у вигляді системи двох різницевих (як правило, нелінійних) рівнянь виду
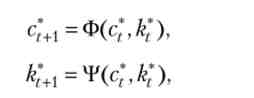
де вид функцій Ф і Т визначається явним видом функцій і /. У загальному випадку, сімейство рішень такої системи залежить від двох вільних параметрів, але двох граничних умов (&0 = &0 і = 0) достатньо, щоб отримати єдине економічно осмислене рішення. При цьому початкове значення капіталу задано явно, а початкове значення споживання неявним чином виходить з умови, що економіка, описана цією системою, повинна в кінцевий момент часу задовольняти умові +1 = 0.
Нескінченний горизонт планування
Розглянемо тепер задачу (В.1) для випадку Т = °°. Завдання на нескінченному обрії планування вирішуються тим же самим методом, що і скінченномірні завдання, хоча при цьому і виникають деякі додаткові тонкощі. Однак для нескінченновимірної завдання теж можна виписати функцію Лагранжа і сформулювати необхідні і достатні умови оптимальності.
З тих же причин, що і в скінченномірному випадку, ми можемо проігнорувати умови невід'ємності для ct і kt + x (Тепер уже на всьому нескінченному проміжку, оскільки тут немає термінального часу Г, після якого зберігати вже свідомо не потрібно). Введемо знову множники Лагранжа (qt) 7 = o Для бюджетних обмежень ct + &,+1 ^ / (&,). Функція Лагранжа для нескінченновимірної завдання має наступний вигляд:
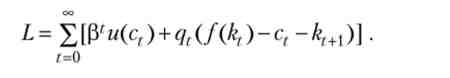
За аналогією з конечномерной завданням, випишемо умови Куна - Так-кер, які повинні виконуватися для всіх t > 0:

Міркуючи так само, як і вище, ми отримуємо, що оптимальна траєкторія характеризується виконанням бюджетних обмежень як рівностей і умовами першого порядку (рівнянням Ейлера):
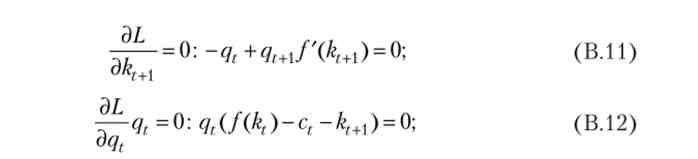
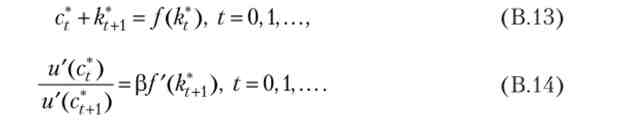
Однак тепер цих умов недостатньо для вирішення вихідної задачі. У нас як і раніше є гранична умова на початку, = k0, але немає граничної умови на іншому кінці, тому що час в цьому завданні не закінчується. Можна сказати, що умови першого порядку визначають, що буде оптимально при русі від одного періоду часу до наступного, але не можуть охопити всю траєкторію цілком. Для того щоб визначити оптимальну траєкторію, потрібно ще одна умова, яке було б аналогом формули (В.8) в скінченномірному випадку.
Згадаймо, що на кінцевій траєкторії має виконуватися рівність (В.6), PjkT + x = 0, яке говорить про те, що приведена вартість капіталу (так як множник Лагранжа має сенс тіньової ціни) в термінальний момент часу повинна дорівнювати нулю. Використовуючи (В.4) і (В.2), це рівність можна переписати у вигляді
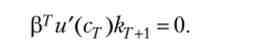
Переходячи в цьому виразі до межі при ми отримуємо потрібну
нам умову, яке носить назву умови трансверсальності:

За змістом ця умова означає, що на оптимальної траєкторії можна занадто багато зберігати. Якби в межі приведена вартість капіталу була позитивна, то це означало б, що агент може зменшити свої заощадження і, не порушуючи бюджетних обмежень, спожити в якийсь момент більше, збільшивши свою корисність (цільову функцію).
Можна показати, що для нескінченновимірних задач умови першого порядку і умова трансверсальності завжди є достатніми умовами оптимальності. При деяких додаткових умовах на функцію корисності (потрібно, щоб її похідна в нулі зростала не дуже швидко), цей же набір умов є і необхідним для оптимальності. Ці додаткові умови не виконуються тільки в спеціальних і дуже рідкісних випадках. Для всіх економічно осмислених проблем і «хороших» функцій корисності - до таких, зокрема, відносяться кінцеві в нулі функції (І (0)> - *) і функції з постійною еластичністю міжчасового заміщення (w (c) = (c1_v-1) / (1-v), Ocv ^ l і w (c) = lnc) - необхідність теж виконується.
Таким чином, для переважної більшості нескінченновимірних задач виду (В. 1), рішення повністю задається умовами (В.13) - (В.15). Для таких завдань, з «хорошими» функціями корисності, можна сформулювати наступне твердження.
Пропозиція В.1. Послідовність (ct,k 't + [) T = Q при заданому початковому значенні &0 = kd є рішенням задачі (В.1) на нескінченному обрії тоді і тільки тоді, коли виконуються умови (В.13) - (В.15).