| Головна |
| ЗМІСТ | Наступна » |
|---|
Розглянемо динамічну систему, задану диференціальним рівнянням

де тек ", а відображення /: До" - "R" має всі властивості, необхідними для того щоб рішення цього рівняння існувало для досить великого безлічі початкових станів. Точкою над х позначається похідна по часу.
Точка х називається станом рівноваги, якщо / (х) = 0, т. Е. Якщо x (t) -x, о), є рішенням рівняння (А.1). стан рівноваги х називається (локально) асимптотично стійким, якщо для всіх початкових значень, що лежать в деякій околиці точки х, динамічна система сходиться до х (інакше кажучи, 35 > 0, таке, що з || л '0 - х ||<8 випливає, що рішення x (t) рівняння (А.1) з початковою умовою x (0) = х0 сходиться до х при t-> °°). Якщо така збіжність має місце для будь-якого початкового х0, то х називається глобально асимптотично стійким.
Розглянемо спочатку найпростіший одномірний випадок (П = 1), припускаючи, що функція / задана на деякому інтервалі (А, Ь) і задовольняє на цьому інтервалі стандартних умов теорем існування та єдиності розв'язку. Припустимо, крім того, що на інтервалі (А, Ь) є єдине рішення х рівняння / (х) = 0, причому ах х => / (Х)> 0; ххЬ => / (Х)< 0.
Пропозиція А.1. Нехай x (t) - рішення даного рівняння
для х (0) е (й, Ь). Тоді x (t) -> х, т. е. стан рівноваги х є гло-
г-»°°
боляче асимптотично стійким.
Деяким аналогом цього твердження в дискретному часі служить наступна пропозиція.
Пропозиція А.2. Нехай на інтервалі (А, b) задані дві безперервні монотонно зростаючі функції ф (. г) і ф (х). Нехай, далі, рівняння ср (х) = | / (. г) має на (а, Ь) єдине рішення х, причому йхх => ф (х)> | / (х); ххЬ = $ ф (х) < ф (х). Тоді будь-яка послідовність (Х,)/ = 01 постро
енная за правилом
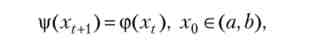
сходиться до х.
Зауважимо, що умова монотонності функцій ф (х) і V | / (x) є в дискретному випадку істотним, хоча його і можна значною мірою послабити.

де А - лінійне відображення, яке ми будемо ототожнювати з його матрицею в природному базисі. Рівняння має принаймні один стан рівноваги, а саме х = 0. Стан рівноваги х = 0 системи (А.2) глобально асимптотично стійко тоді і тільки тоді, коли речові частини всіх власних чисел матриці А негативні.
Затвердження А.2. Розглянемо систему (А.1) в загальному вигляді. нехай х - її стан рівноваги. Ми припускаємо, що функція / неперервно диференційовна. Позначимо через А (х) матрицю приватних похідних відображення / в точці х. Для локальної асимптотичної стійкості стану рівноваги досить, щоб речові частини всіх власних чисел матриці А (х) були негативні.
Нагадаємо, що число А. називається власним числом матриці А, якщо Ах = ХХ для деякого х ^ 0, або, інакше, якщо це число є рішенням рівняння А-1= 0, де I - одинична матриця. У двовимірному випадку, т. Е. При п = 2, перевірити (локальну) асимптотичну стійкість рівноваги щодо просто, так як можна помітити, що речові
(а a12l
частини всіх власних чисел матриці А = Негативні тоді
a2i а22)
і тільки тоді, коли її слід негативний, а визначник позитивний. Іншими словами, має виконуватися +а22 <0 і апа22 ~ а2а2 > 0- Двовимірний випадок зручний ще й тим, що умови глобальної асимптотичної стійкості є безпосереднім узагальненням умов локальної асимптотичної стійкості. А саме, має місце наступна пропозиція.
Пропозиція А. З. Розглянемо систему (А.1) в припущенні, що п - 2. Для глобальної асимптотичної стійкості стану рівноваги х досить, щоб для всіх х речові частини всіх власних чисел матриці А (х) були негативними, т. Е. Щоб виконувалися
з /, е /2 _ Е /, е /2 а /, е /2 _ Е /, е /2 _
нерівності -^ + - ^ -<0, -> 0, а крім того, 1 ^ 0 або
ОХ] Ех2 ОХ] Ех2 Ех2 Ех, ех, ех2
Ех2 Ех,