
| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Модель Рамсея є моделлю екзогенного зростання. Вона має схожу структуру з моделлю Солоу, зокрема, в ній виконуються вже відомі нам співвідношення: випуск, що задається неокласичної виробничої функцією,

ділиться на споживання та інвестиції,
запас капіталу дорівнює

де р - це норма амортизації, а темп зростання робочої сили (яка збігається з усім населенням) постійний:
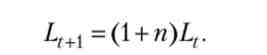
Зараз ми для простоти викладу будемо припускати, що технічного прогресу немає (його темп приросту дорівнює нулю): 1 = Aq = Ai = ... = At = ... . Таким чином, темп приросту ефективної робочої сили збігається з темпом приросту робочої сили п. Крім того, будемо вважати, що капітал протягом одного періоду вибуває повністю (р = 1).
важливо запам'ятати
Може здатися, що припущення про повну вибутті капіталу протягом одного періоду не дуже реалістично. Але змістовно воно може означати, що в якості періоду часу t береться не один рік, а, скажімо, п'ять років. Тоді припущення про те, що майже весь капітал поточного періоду не може бути використаний в наступному, більш виправдано. Це зайвий раз підкреслює принципово довгостроковий характер всіх моделей економічного зростання.
З огляду на все вищесказане, основні співвідношення, яким задовольняє модель Рамсея, можна переписати так:

Перейдемо до питомою величинам, традиційно позначаючи їх відповідними малими літерами. Розділивши перше з цих співвідношень на Lt, ми отримаємо

Як і в разі моделі Солоу, при заданому L0 по послідовності КАПИТАЛОВООРУЖЕННОСТЬ (? Д=про, 1, ... ми можемо однозначним чином вказати значення всіх цікавлять нас змінних (як питомих, так і валових) в будь-який момент часу. Але все одно для зручності під траєкторіями в моделі Рамсея ми будемо розуміти послідовності КАПИТАЛОВООРУЖЕННОСТЬ і питомих потреблений, (kn ct)t = 0л .
Важливою відмінністю моделі Рамсея є механізм формування норми заощадження. У моделі Солоу робилося найпростіше припущення про те, що заощадження, а значить і споживання, становлять постійну частку випуску. Тоді рівність (20.1) перетворювалося в рівняння динаміки послідовності КАПИТАЛОВООРУЖЕННОСТЬ. Але поглянемо на рівняння (20.1) докладніше. Фактично воно означає, що сьогоднішній випуск f (kt) треба розділити на сьогоднішнє споживання ct і інвестиції в фактор виробництва (фізичний капітал kt + 1), що дозволить виробити продукцію завтра. При цьому, чим менше агенти витратять на споживання сьогодні, тим більше вони інвестують. Тоді тим більшим буде завтрашній випуск, що може забезпечити більш високий рівень споживання. Таким чином, агенти повинні приймати рішення про те, скільки зберігати, якимось чином порівнюючи поточне і майбутнє споживання.
Припустимо, що нам відома миттєва (короткострокова) функція суспільної корисності і: До+ -> М, яка ставить у відповідність рівню питомого споживання з в суспільстві на певному одиничному проміжку часу величину суспільної корисності і (з) Зазвичай передбачається, що ця функція двічі неперервно диференційовна всередині своєї області визначення, монотонно зростає (і' > 0), строго ввігнута (І " 0), а також задовольняє умовам Инада (lim і '(с) = + °°у lim і '(с) = 0).
з-> 0 з -> °°
Припустимо також, що заданий громадський коефіцієнт дисконтування Р (0<(3<1), за допомогою якого порівнюється корисність від споживання в різні моменти часу. В цьому випадку в поточний (нульовий)
оо
момент часу цільова функція суспільства є? (3'і (СД Вона поставала
ляє собою дисконтовану суспільну корисність на нескінченному інтервалі часу. Зверніть увагу, що | 3 '- це Р в ступеня t. Нижній індекс часу t ми використовуємо для того, щоб позначати змінні, що відносяться до моменту або періоду t. А в разі, коли індекс часу варто вгорі, він показує ступінь, в яку зводиться те чи інше число.
важливо запам'ятати
Міжчасового переваги суспільства визначаються коефіцієнтом дисконтування р. Цей коефіцієнт можна інтерпретувати як ступінь «нетерплячості» суспільства - то, наскільки сильно або слабо дане суспільство цінує своє майбутнє. Наприклад, рівність нулю цього коефіцієнта (Р = 0) означає абсолютну нетерплячість або «короткозорість», при якій майбутнє споживання не має взагалі ніякої цінності з точки зору сьогоднішнього дня. Чим вище р, тим більш терплячим є суспільство. Інший граничний випадок, абсолютної терплячості (Р = 1), означає, що одиниця корисності від будь-якого споживання в майбутньому так само важлива для агента, як і одиниця корисності від сьогоднішнього споживання. Відразу ж уточнимо, що в рамках моделі Рамсея обидва граничних випадки не розглядаються. Випадок Р = 0 беззмістовний, так як означає, що суспільство споживе все в початковий момент часу. У разі ж р = 1 рішення задачі про максимізації оо
дисконтированной корисності? м (з,) не існуватиме. Відзначимо, що в рамках
?= про
моделі Рамсея коефіцієнт дисконтування суспільства передбачається постійним і заданим, а питання про його формуванні практично ніколи не розглядається.
А
При заданому початковому значенні капиталовооруженности = до0, задача оптимального економічного зростання в моделі Рамсея на нескінченному обрії планування має такий вигляд:
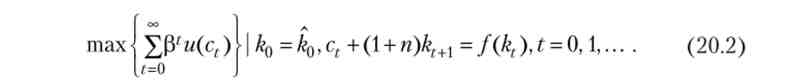
Можна показати, що, оскільки (3<1, рішення цього завдання існує, а в силу суворої увігнутості функції f (k) Він єдиний. послідовність (K *t,c *t)t = 0 t, є рішенням задачі (20.2), називається оптимальною траєкторією в моделі Рамсея (що виходить із початкового
А
стану до0). Нескладно перевірити, що в силу умов Инада капиталовооруженность до * і питоме споживання ct є позитивними числами для всіх t = 0,1, ___
послідовність (До * Уз *)1 = 0 { є рішенням задачі (20.2) тоді і тільки тоді, коли виконуються наступні співвідношення (див. Пропозиція B.1 в математичному додатку В):
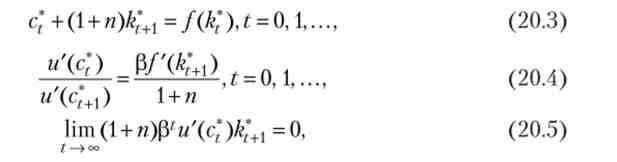
і при цьому = k0. Набір рівності (20.3) являє собою бюджетні обмеження завдання. Співвідношення (20.4) відомі як умови першого порядку. Нарешті, (20.5) називається умовою трансверсальності. Рівняння (20.3) - (20.5) повністю визначають оптимальну траєкторію.