
| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Економічна теорія пов'язує будь-демографічні зміни перш за все з ресурсними і виробничо-технологічними змінами, а зростання населення з результатами розвитку економічних відносин і зростання продуктивності праці. Основне положення теорії народонаселення було сформульовано ще в XVIII ст. англійським вченим Томасом Мальтусом: «Протягом більшої частини існування людства зростання його чисельності на кожен даний момент часу був обмежений стелею несучої здатності землі, обумовленим спостережуваним в даний момент часу рівнем розвитку життєзабезпечуючих технологій».
Розглядаючи проблеми, пов'язані з ростом народонаселення, Мальтус припустив, що швидкість росту населення dN / dt за відсутності стримуючих факторів пропорційна чисельності населення N, де t - час. Це припущення приводить до наступної моделі:

де iV0 - чисельність населення в початковий момент часу; а - коефіцієнт пропорційності (різниця між постійними коефіцієнтами народжуваності та смертності).
Це рівняння має наступне рішення:
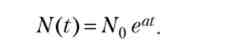
Відповідно до нього населення подвоюється через проміжки часу, рівні 1п2 / а. З рішення випливає, що N (t) -При. Це говорить про те, що область застосування моделі звужена: при великих значеннях N слід враховувати обмежуючі фактори.
Іншими словами, рішення рівняння пророкує експоненціальне зростання популяції, відомий як мальтузіанський зростання, якщо а > 0 (коефіцієнт народжуваності перевищує коефіцієнт смертності), або експоненціальне спад популяції, якщо а < 0 (смертність перевищує народжуваність).
У 1838 р бельгійський матемаік Ферхюльст запропонував логістичну модель, яка більш вірогідно описує динаміку популяцій. Це була спроба описати демографічні моделі за допомогою добре зарекомендували себе популяційних моделей, що використовуються в біології. Відповідне рівняння має вигляд
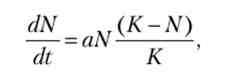
де К - ємність екологічної ніші популяції, т. е. гранична чисельність, якої може досягти популяція. параметр До має принципове значення. Він визначає рівноважний стан в динаміці популяції при заданих ресурсних обмеженнях і межі її зростання. Коли чисельність популяції мала (N «К), рівняння збігається з моделлю і чисельність популяції наростає експоненціально (за умови, що а > 0). Народжуваність приймається постійною, таким чином, число народжень пропорційно чисельності популяції. Природна смертність також вважається постійною, але обмеженість ресурсу не дозволяє популяції нескінченно зростати. У міру збільшення N позначається дію обмежуючих факторів, швидкість зростання популяції зменшується, і при? -> оо чисельність популяції кине до К, а швидкість росту популяції dN / dt - до нуля. Рівняння має два стани рівноваги, одне з них (N = 0) є нестійким, а друге (N = К) - стійким. У стаціонарному стані в будь-який момент часу число народжень дорівнює числу смертей, але з плином часу параметри моделі можуть змінюватися. В результаті динаміка популяції приймає наступний вигляд: коли чисельність тварин мала, спостерігається експоненціальне зростання з показником а (коефіцієнт пропорційності), потім у міру заповнення екологічної ніші зростання сповільнюється і в кінцевому рахунку чисельність популяції виходить на постійний рівень.
Іншою моделлю, яка описує динамку популяцій двох взаємодіючих видів, один з яких є основною їжею для іншого, є модель Лотки - Вольтерри, відома як «хижак - жертва». Її можна застосувати для опису коливань чисельності населення, виявлених практично у всіх аграрних суспільствах. У ролі жертви виступає населення, а в ролі хижака - соціальна нестабільність, війни, голод, епідемії, ймовірність виникнення яких збільшується в міру того, як зростаюче населення наближається до стелі несучої здатності.
Модель описується двома рівняннями

де х - чисельність жертв; у - чисельність хижаків; А, В, С, D - коефіцієнти.
Дана модель, гак само як і попередня, передбачає, що число народжень жертв пропорційно їх чисельності. Число смертей хижаків також пропорційно їх чисельності. Що ж стосується смертності жертв і народжуваності хижаків, то тут виникає системний ефект. Вважається, що жертви в основному гинуть через контакт з хижаком, а народжуваність хижаків залежить від наявності їжі - жертв. У моделі передбачається, що в середньому число контактів жертв і хижаків пропорційно чисельності обох популяцій. Дана модель демонструє циклічну динаміку. Зростання чисельності жертв призводить до зростання хижаків, зростання хижаків викликає скорочення жертв, скорочення жертв веде до скорочення хижаків, а при малій кількості хижаків жертви знову починають бурхливо розмножуватися.