| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Стандартна модель Бертрана передбачає досконалу заменимость товарів двох і більше фірм і, як наслідок, надзвичайно високий ступінь цінової конкуренції. Що ж станеться на ринку, якщо фірми можуть виробляти різнорідну (диференційовану) продукцію?
Припустимо, на ринку, відповідному характеристикам конкуренції по Бертрану, діє дві ідентичні фірми. Попит на товар кожної з них описується наступним рівнянням:
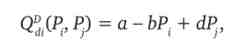
де Р - ціна, що призначається даною фірмою; Р - ціна фірми-конкурента; причому: 0 < d < b, а > c {b - d).
Ці додаткові умови гарантують отримання розум-ного результату - неотрицательной прибутку, існування ринку, реакцію споживачів насамперед на товар даної фірми і потім (при різних цінах) на диференційований товар іншої фірми.
Нехай витрати на одиницю товару в обох фірм ідентичні, постійні і рівні з > 0.
Тут ми бачимо, що товари двох фірм (г і j) служать недосконалими замінниками один одного. Пряма цінова еластичність попиту на товар негативна, перехресна еластичність попиту на товар позитивна (що випливає з знаків коефіцієнтів при цінах).
якщо ціна Р досить велика в порівнянні з ціною Р, то обсяг попиту на товар i дорівнює нулю. Однак при невеликій різниці цін навіть якщо ціна конкурента перевищує ціну даної фірми, якась частина покупців залишиться «правильна» цього товару. У цьому випадку мова йде про явище лояльності споживачів - прихильності покупців однієї і тієї ж марки товару.
Умова d < ред означає, що якщо ціни товарів обох фірм виростуть на нескінченно малу величину е, обсяг попиту на обидва товари скоротиться.
Умова а > c (b - d) Означає, що якщо обидві фірми призначать ціни на рівні граничних витрат, обсяги попиту на їхні товари будуть позитивними.
Визначимо результат такої взаємодії фірм. Знайдемо такий набір цін (Р *, Р *), що Р * забезпечує максимізацію прибутку
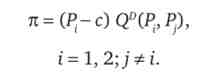
Для цього обчислимо для будь-якого Р( функцію реакції г-й фірми, максимізує результат (Р с) - Qd(P, Р). Функція реакції покаже, яким чином одна фірма змінює свою ціну в залежності від того, яку ціну призначає її конкурент.
Нехай Р, (Р) - функція реакції фірми на ціну конкурента. Для розглянутого нами прикладу функція реакції матиме вигляд
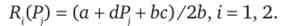
Функції реакції обох фірм симетричні, так як вони ідентичні. Вирішивши систему з двох рівнянь для функцій реакцій фірм, отримаємо наступний результат:
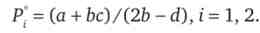
При такій комбінації цін двох фірм вони будуть отримувати позитивний прибуток, так як різниця між рівноважною ціною і граничними витратами позитивна для кожної фірми:
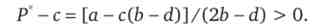
Отже, ми бачимо, що диференціація продукту пом'якшує цінову конкуренцію, так що суперництво фірм не веде до повного зникнення їх прибутків.
Проаналізуємо докладніше функції реакції фірм в моделі Бертрана.
Вибір фірм здійснюється щодо цін. Типові функції реакції (R) Для ринку диференційованого товару, згідно вище наведеними формулами, будуть виглядати так, як показано на рис. 15.2.
Що станеться при зниженні ступеня продуктової диференціації?
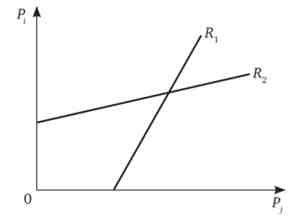
Мал. 15.2. Звичайні функції реакції в моделі Бертрана з диференційованим продуктом
Кути нахилу функцій реакції будуть зменшуватися аж до того моменту, поки не виявляться рівними один одному і лінії під кутом 45 ° (рис. 15.3).
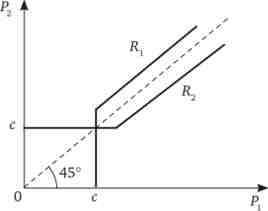
Мал. 15.3. Функції реакції при однорідному продукті
Малюнок 15.3 показує, що рівновага в цінах при однорідному продукті фірм буде спостерігатися в точці перетину функцій реакції фірм при однакових цінах, рівних витратам, т. Е. Ми отримали такий же результат, як і раніше при аналітичному аналізі. Якщо яка-небудь фірма відхиляється від цієї рівноважної ціни вгору, її конкурент може проводити стратегію «підриву», призначивши свою ціну трохи нижче ціни першої фірми. Чим вище ціна «відхилення» однієї фірми, тим більше може бути і ціна «підриву».
Слід також звернути увагу, що чим вище ступінь диференціації продукту, т. Е. Чим менше замінними виявляються товари різних фірм в очах покупців, тим більше розбіжність між кривими реакції, так як тим в меншій мірі цінова поведінка однієї фірми буде впливати на цінову стратегію інший фірми. У граничному випадку обидві фірми будуть локальними монополіями, а криві їх реакції - прямими, паралельними відповідним координатним прямим (рис. 15.4). Рівновага на ринку в даному випадку - це монопольні ціни фірм.
Таким чином, результат цінової конкуренції олігополістів залежить в першу чергу від характеристики товару - виробляють фірми однорідний або диференційований продукт.
Цінова конкуренція при обмеженнях на потужності фірм
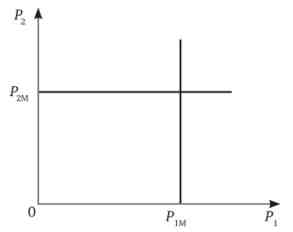
Мал. 15.4. Функції реакції при найвищого ступеня продуктової диференціації на ринку
модель Еджуорт є модифікацією моделі Бертрана, яка показує ситуацію цінової конкуренції фірм з обмеженими розмірами випуску. Розглянемо, яким чином в цих умовах буде відбуватися цінове взаємодія двох фірм і яким чином фактор обмеженості сукупних потужностей фірм впливає на встановлення рівноваги на ринку.
Історична довідка
Френсіс Еджуорт (1845-1926), британський економіст ірландського походження. Закінчив Трініті-коледж в Дубліні і Оксфордський університет (Велика Британія). Початкову освіту отримав в області класичної літератури. Самостійно освоїв математику та економіку. Викладав в Оксфорді. Був президентом Королівського статистичного товариства і одним із засновників Британської академії в 1903 р, редактор Economic Journal. Виступав за активну і універсальне використання математики в економічній теорії. Вніс великий внесок у розробку теорії загальної рівноваги конкурентних ринків.
Нехай попит на ринку дорівнює: Р - 1 - Q (де Q - загальний обсяг пропонованого до продажу однорідного товару). На ринку діє дві однакові фірми з рівними граничнимивитратами. Але виробничі потужності фірм обмежені, тому при ціні, рівної граничним витратам, одна фірма не змогла б задовольнити весь попит:
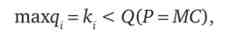
де к. - межа потужності фірми.
Покажемо, що ціна на рівні Рг = Р2 = МС не є більш рівноважною ціною ринку. Нова рівноважна ціна буде дорівнює: Р = 1 - до - до > МС. Фірми в цих умовах отримають позитивну прибуток!
Нехай фірма 2 призначає ціну на рівні граничних витрат Р2 = МС. Тоді фірма 1 може призначити трохи вищу ціну: Р1 = МС + е, е> 0.
Що при цьому відбудеться на ринку? Всі покупці, звичайно, захочуть купити товар тільки у фірми 2. Однак ця фірма внаслідок наявності обмеження по потужності не зможе задовольнити весь попит за даною ціною: D2 = k2< D {P = MC). І фірма 1 зможе також продати певну кількість товару (залишковий попит): D, = D - до2 > Про - за ціною вище граничних витрат, в результаті чого вона отримає позитивну прибуток. Отже, по крайней мере, у фірми 1 є стимули до відхилення від граничного ціноутворення. Тому ціна, яка дорівнює граничним витратам, тепер не буде рівноважною ціною.
Нехай тепер фірма 2 призначає ціну на рівні: Р2 = Р = l- kl-k2 МС. В цьому випадку вона отримає позитивну прибуток. Чи є стимули у фірми 1 призначити іншу ціну?
Якщо фірма 1 призначить ціну Р} нижче ціни Р2, то вона нічого не виграє в обсязі продажів, тому що її потужності не дозволять розширити збут більше, ніж qx = kv т. е. такий же збут, що і при ціні Рг = Рг При цьому ціна фірми 1 буде нижче, отже, сукупний прибуток від її продажу скоротиться: п1(Р1 < Р2) < л ^ = Р2). Дане відхилення не є прибутковим для фірми 1, так як воно не буде здійснено.
Якщо фірма 1 призначить ціну Р1 вище ціни Р2, то її залишковий попит складе
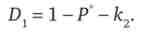
Прибуток фірми 1 буде дорівнює: = Р, - (1 - Р, - до2). або пх = (1 - -
-k2) ql.
Наявність обмеження на потужності фірм означає діяльність фірм до точки падіння прибутку, т. Е. Функція прибутку в даному діапазоні буде зростаючій по відношенню до обсягу виробництва. Якщо фірма 1 призначає вищу ціну, ніж ціна фірми 2, вона зможе продати відповідно до закону попиту менший, ніж дох обсяг товару. А це знову-таки призведе до падіння її сукупного прибутку: < n^kj.
Отже, призначення більш високої ціни теж не буде прибутковим відхиленням від рівноваги, і воно так само не матиме місця.
Таким чином, при встановленні ціни на рівні, що забезпечує повне завантаження потужностей обох фірм, ні в однієї з фірм не буде стимулів відхилятися від рівноваги. Це і буде нова рівноважна ціна.