| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Якими повинні бути витрати фірми, щоб зробити заданий обсяг продукції з мінімальними витратами (найбільш ефективним чином)?
Незмінний випуск задається изоквантой. Лінія витрат характеризує рівень витрат на фактори виробництва при ринкових цінах ресурсів. Ця лінія називається изокоста - лінія однакових витрат. Наприклад, для випадку двох ресурсів - праці і капіталу - изокоста приймає наступний вигляд: ТС = w-L + r-K, де w - ціна одиниці праці; г - ціна одиниці капіталу. Під ціною праці можна розуміти погодинну ставку заробітної плати або середню заробітну плату одного працівника за період часу (наприклад, за місяць). Ціна капіталу - це альтернативні витрати використання грошей, ставка по кредиту або ставка орендної плати за використання обладнання.
Поставимо задачу для фірми: тт'ГСЦС, L) для досягнення Q = Q *. Нехай для визначеності виробнича функція представлена у вигляді: Q = KU 1 ?.
Побудуємо функцію Лагранжа
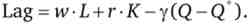
Точка оптимуму повинна задовольняти умовам першого порядку:
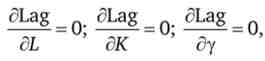
де у - множник Лагранжа.
Для випадку двох факторів виробництва оптимальне рішення може бути знайдено також на основі аналізу графіка (рис. 12.5).
Оптимальний вибір обсягу ресурсів, що мінімізує витрати при випуску певного обсягу продукції, знаходиться в точці дотику ізокванти і ізокости. Це відповідає частці від ділення двох перших рівнянь в умовах першого порядку функції Лагранжа.
Нахил ізокванти дорівнює граничній нормі технологічного заміщення, т. Е. Стосовно граничних продуктів факторів виробництва:
MRTS = ^L.
МРДо
Нахил ізокости показує відношення цін одиниці ресурсів: (iv / r).
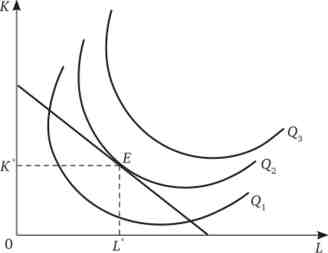
Мал. 12.5. Оптимум фірми як мінімізація її витрат
_. МР, iv "
Прирівняємо ці два вирази один до одного: MRTS = -- = -. Для вихідної виробничої функції отримаємо МРдо г
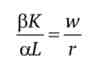
або
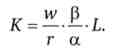
Підставами даний вираз у функцію обмеження - функцію ізокванти
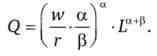
Звідки знайдемо оптимальне значення обсягу найманого праці
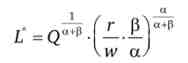і оптимальне значення обсягу найманого капіталу
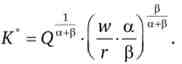
Проаналізуємо уважно функції оптимальних обсягів ресурсів. Як можна помітити, кожна функція являє собою зворотну залежність між ціною відповідного ресурсу і обсягом найманого фактора виробництва. Ця залежність називається «умовний попит на ресурс». Чому попит на ресурс? Оскільки взаємозв'язок типу «ціна - обсяг покупок» в мікроекономіці характеризує попит на товар, то в даному випадку буде попит фірми на ресурс. Чому умовний? Тому що тут мова йде не про реальний ринок, де вибір пов'язаний не тільки з об'ємом продукції, що продається, а й з її ціною, а про умовне ринку. Такий попит на ресурс за умови, що заданий цільовий обсяг продукції буде проданий на ринку.
У загальному вигляді умовний попит на фактор виробництва може бути представлений таким чином: X, = f (Pt, Pjy Q), гдеX - обсяг використовуваного ресурсу; Р. - ціна даного ресурсу; Pj - ціни інших ресурсів.
Повернемося до точки оптимуму фірми. Перерозподіливши граничні продукти і ціни ресурсів, запишемо умову оптимуму наступним чином:
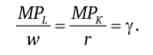
Цей вислів можна назвати «еквімаржінальний принцип у виробництві» за аналогією з еквімаржінальним принципом вибору споживача. Еквімаржінальний принцип у виробництві говорить про те, що для мінімізації витрат фірма повинна розподілити свої витрати таким чином, щоб останній вкладену гривню приносив однакову віддачу від кожного використовуваного ресурсу. Показник у (множник Лагранжа в задачі знаходження умовного мінімуму витрат фірми) оцінює граничну продуктивність грошей.
У загальному вигляді розв'язок задачі мінімізації витрат підпорядковується умовам Куна - Таккера.
якщо Pi= Y-MPi (Ціна ресурсу відповідає граничної віддачі від ресурсу в грошовому вигляді), то X * > 0, ресурс купується. Тут буде спостерігатися внутрішній оптимум фірми.
якщо Р{ > у - МР( (Ціна ресурсу перевищує граничну віддачу від нього в грошовому вигляді), то X? = 0, ресурс не купується. Тут ми маємо кутовий рішення.
Завдання, що ілюструє теорію
Фірма платить 50 тис. Руб. в день працівникам і 200 тис. руб. за оренду обладнання. Фірма наймає таку кількість праці і капіталу, що граничний продукт капіталу дорівнює 4 тис. Шт., А граничний продукт праці - 8 тис. Шт. Фірма випускає 500 тис. Шт. товару в день. Чи використовує фірма оптимальне поєднання чинників виробництва? Якщо немає, що їй треба зробити, щоб поліпшити своє становище?
Рішення
Оптимальне співвідношення факторів виробництва визначається еквімаржінальним принципом у виробництві: додаткова грошова одиниця, витрачена на будь-який чинник виробництва, приносить однакову граничну віддачу.
Тому відносини граничних продуктів факторів виробництва до цін ресурсів повинні бути постійні для всіх використовуваних ресурсів:
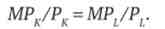
Перевіримо, чи виконується це співвідношення для даного випадку:
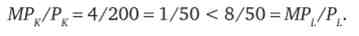
Тут еквімаржінальний принцип не виконується. Це означає, що фірма не використовує оптимальне співвідношення факторів виробництва. Щоб досягти оптимального співвідношення ресурсів, фірма повинна збільшити обсяг застосовуваного праці і скоротити обсяг використовуваного капіталу. В такому випадку з ростом обсягу застосовуваного праці граничний продукт праці скоротиться (відповідно до закону спадної граничної продуктивності); а з скороченням обсягу використовуваного капіталу граничний продукт капіталу збільшиться. Дану політику слід продовжувати до тих пір, поки рівність відносин граничних продуктів до цін ресурсів не буде відновлено.
Особливо слід відзначити, що кількісне значення випуску не має ніякого значення для визначення оптимального співвідношення факторів виробництва.
Можна поставити задачу по-іншому. Якщо в заданий період часу фірма виділила для будь-якого виробництва певну суму грошей (свого роду бюджет виробництва), то як фірмі розподілити кошти між факторами виробництва для максимізації сукупного випуску?
Ця проблема є двоїстої завданням виробництва. Її рішення може бути знайдено за допомогою функції Лагранжа і використанням еквімаржінального принципу у виробництві: maxQ (K, L) при обмеженні ТС = w-L + r-К. При одних і тих самих вихідних умовах графік на рис. 12.5 буде показувати оптимум і в цьому випадку.
Для функції Кобба - Дугласа оптимальний обсяг праці тут буде дорівнює
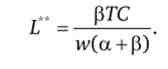
Оптимальний обсяг капіталу
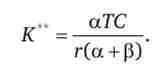
Підставами оптимальні значення у вихідне вираз для виробничої функції:
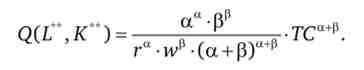
Позначимо параметр перед ТС буквою N. Висловимо сукупні витрати
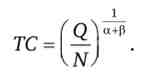
Ця функція характеризує мінімальні (ефективні) витрати при будь-якому рівні виробництва. Дану функцію можна назвати функцією мінімальних витрат.
Зауважимо, що якщо в прямій задачі мінімізації витрат ми підставимо в вихідну функцію витрат
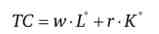
оптимальні значення обсягів ресурсів (умовний попит на ресурси), то отримаємо одну і ту ж функцію мінімальних витрат
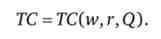
Функція мінімальних витрат має такі властивості.
1. Функція має однорідністю першого ступеня щодо цін ресурсів:
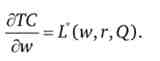
Похідна функції витрат за ціною ресурсу дорівнює умовному попиту на цей ресурс.
Докази цих властивостей аналогічні доказам властивостей функції мінімальних витрат в теорії поведінки споживача.
Лемма Шепарда для виробництва показує вплив зміни ціни ресурсу на сукупні витрати фірми. Якщо ціна фактора виробництва зростає, то сукупні витрати фірми стають більше на величину, рівну початкового обсягу цього фактора.
А як впливає ціна ресурсу на граничні витрати?
Розглянемо динаміку граничних витрат:
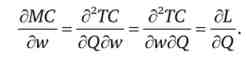
Ми використовували властивість інваріантності друге змішаних похідних і лемму Шепарда. Таким чином, зміна граничних витрат під дією зростання або падіння ціни ресурсу залежить від того, до якого типу ресурсу відноситься змінний фактор.
Введемо класифікацію факторів виробництва.
якщо dL / dQ> 0 (зростання випуску вимагає збільшення ресурсу), то ресурс вважається нормальним (якісним) фактором виробництва.
якщо dL / dQ < 0 (у міру збільшення випуску фірма позбавляється від ресурсу), то ресурс розцінюється як неякісний фактор виробництва.
якщо dL / dQ = 0 (фірма не змінює обсяги використовуваного ресурсу), то ресурс є нейтральним фактором виробництва.
якщо dQ / dL 0, ми маємо справу з антіресурсом.
Слід зазначити, що серед ресурсів не може бути «товарів Гіффена», оскільки якщо ціна неякісного ресурсу зростає, фірма завжди може скоротити виробництво і, отже, зменшити попит на ресурс. На відміну від індивіда у фірми немає однозначно заданого рівня виробництва.
Отже, при збільшенні ціни змінного фактора граничні витрати зростають, якщо цей фактор - нормальний ресурс, і зменшуються, якщо це - неякісний ресурс.
Яким чином фірмі слід розподілити виробництво, якщо у неї є не один, а кілька заводів?
Тут нам знадобляться умови оптимальності Куна - Таккера.
Нехай фірма хоче мінімізувати сукупні витрати цільового випуску Q *, розподіляючи виробництво між двома заводами з різними, в загальному, функціями витрат.
Запишемо в формальному вигляді завдання фірми
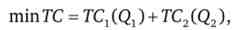
при обмеженнях:
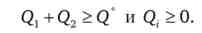
Побудуємо функцію Лагранжа
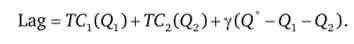
Умови Куна - Таккера такі:
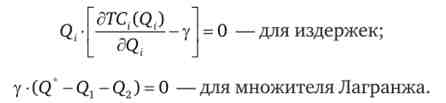
Множник Лагранжа показує ступінь зростання сукупних витрат фірми при збільшенні її сукупного випуску Q *. В даному випадку економічний сенс множника Лагранжа можна визначити як граничні витрати фірми в цілому. Так як фірма щось виробляє хоча б на одному зі своїх заводів, її граничні витрати позитивні. Тому множник Лагранжа позитивний. І це значить, що обмеження на випуск виконується як рівність: Qj + Q2= Q *. Фірма, яка мінімізує витрати, не перевищуватиме цільовий випуск.
Якщо все заводи фірми використовуються (в нашому прикладі випуск положіте-
&ТС (Про)
льон на обох заводах), то Q,> 0 і -* --- у = 0 або MC1(Q1) = MC2(Q2) = '/.
dQi
Фірма так повинна розподілити випуск між своїми заводами, щоб граничні витрати виробництва на кожному з них були рівні між собою.
ajvj / q л
Якщо для будь-якого заводу - * - - у > 0, т. Е. Граничні витрати
dQi
непропорційно великі, то цей завод слід закрити: Q, = 0.
Завдання, що ілюструє концепцію
Ваша фірма належать два заводи, що випускають однорідний товар. Сукупні витрати випуску на першому заводі складають
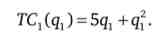
На другому заводі сукупні витрати дорівнюють
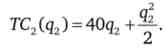
Рішення
1. Знайдемо граничні витрати кожного заводу
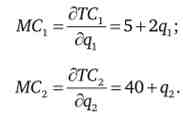Скористаємося умовами оптимуму
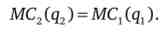
Відомо, що планується продати 25 тис. Од. товару, тоді
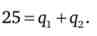
Вирішуючи два рівняння з двома невідомими, отримуємо оптимальні обсяги виробництва для кожного заводу: q, = 20; q2= 5.
2. Відомо, що планується продати 15 тис. Од. товару, тоді
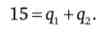
Вирішуючи аналогічним чином, як і в п. 1, нову систему, ми отримуємо, що q2 < 0. Це означає, що витрати на другому заводі занадто великі при такому маленькому сукупному випуску. Другий завод стає неефективним з точки зору фірми, і його слід закрити.
Отже, Q = q, = 15, q2 = 0.