Максимізація корисності. рівняння Ейлера

Інтегральна корисність за нескінченний період часу (U) Дорівнює дисконтованою потоку миттєвої корисності (І). Миттєва корисність є зростаюча функція поточного обсягу споживання (С). Розглянемо миттєву функцію корисності:

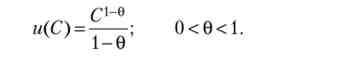
Домогосподарства максимізують інтегральну корисність, варіюючи функцію споживання З:

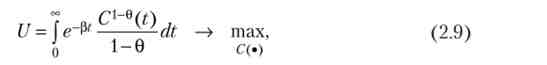
де C (t) - споживання в момент?, (3 > 0 - норма міжчасового переваги, яка в рівність (2.9) виконує функцію суб'єктивної норми дисконтування: чим вона більше, тим менше цінується майбутнє споживання. При нескінченно великому її значенні цільова функція приблизно дорівнює величині корисності в початковий момент часу: U ~ м (С (0 ».

Бюджетне обмеження домогосподарства - теперішня вартість споживання дорівнює сумі початкового багатства і дисконтованого доходу (С - К (0) + VP):

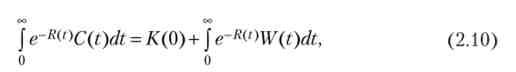
де W - дохід; До - багатство; R - інтеграл від ставки відсотка r (t), яка в рівність (2.10) виконує функцію об'єктивної норми дисконтування.

Для максимізації (2.9) при обмеженні (2.10) продифференцируем функцію Лагранжа L по С, переставляючи знаки диференціала і інтеграла, а потім прирівняємо похідну нулю:

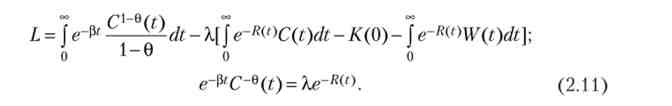
Прологаріфміруем і продифференцируем (2.11):

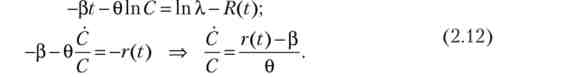
При диференціюванні було використано відоме властивість інтеграла:

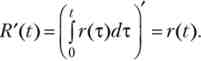
Рівняння (2.12) називають рівнянням Ейлера для даної задачі оптимізації. З нього випливає, що зростання або спадання споживання в часі залежить від різниці об'єктивної (г) і суб'єктивної (Р) норми дисконтування. Нехай ставка незмінно дорівнює г, тоді тими приросту споживання (З / С) дорівнює (г - р) / 0, і рівняння має просте рішення:

якщо г > р, т. з. індивід високо цінує 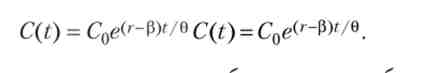оудущес потреоленіе, то його поточне споживання зростає протягом життя. якщо г < р, т. е. індивід низько цінує майбутнє споживання, то його поточне споживання скорочується протягом життя. якщо г = Р, то споживання незмінно і одно своєму початковому значенню З₀. Параметр 0 лежить в межах від 0 до 1, а різниця (1 - 0) характеризує чутливість миттєвої корисності до обсягу споживання. Чим більше 0, тим менше чутливість і тим менше темп зміни обсягу споживання.

Якщо ставка відсотка змінюється в часі, то може існувати безліч моментів часу, коли споживання нс змінюється в часі. Вони знаходяться з рівняння r (t) = Р, т. Е. Відповідають точкам перетину кривої r (t) і горизонталі г = р. З (2.12) випливає, що якщо ставка відсотка приймає значення Р при зниженні, то в цей момент часу досягається локальний максимум споживання. Якщо ж вона приймає це значення в процесі збільшення, то досягається локальний мінімум споживання.

приклади

1. Ставка убуває: г = r₀ / (1 + t). Вирішимо рівняння Ейлера:

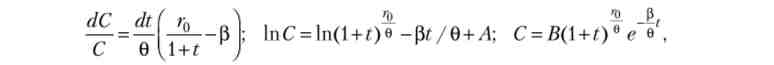
де В - позитивна константа, що залежить від початкового об'єму споживання.

Застосувавши правило Лопіталя при знаходженні межі С (?), Ми приходимо до висновку, що в довгостроковому періоді споживання скорочується і прагне до нуля.

2. Ставка змінюється циклічно: r = 0, lsin? + 0, l; P = 0,15. Тоді з умови г = Р отримуємо два нескінченних безлічі моментів часу з незмінним споживанням:

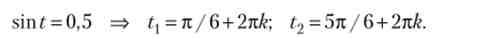
У моменти t_{ ставка зростає, тому споживання має локальний мінімум, в моменти t₂ вона падає, і споживання має локальний максимум.

У загальному випадку рівняння Ейлера враховує також темп приросту населення (П) і темп приросту ефективності праці (g):

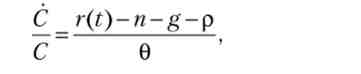
¹ див .: Ромер, Д. Вища макроекономіка. М.: Изд. будинок ВШЕ, 2014. Гл. 2. С. 86.

де р = р - я- (1 -0) g¹.

1. Модель Калдора
   У моделі Калдора, як і в монетарній концепції економічних циклів, причинами циклічного розвитку економіки є ендогенні фактори. В основі цієї моделі лежать специфічні функції інвестицій і заощаджень. И. Калдор виходив з того, що в короткому періоді обсяг інвестицій залежить від величини реального
2. Моделі зростання з людським капіталом, модель з виробництвом людського капіталу
   Людський капітал - якості людини, придбані в процесі освіти або кваліфікованої праці і служать джерелом доходу. В даному підпункті розглядається загальний людський капітал} який формується в процесі навчання в навчальному закладі. В економіці є два сектори. Перший - традиційний, він виробляє
3. Моделі світової економіки, модель конкурентних переваг
   Нехай країна виробляє два продукти (X, Y). Виробнича можливість - набір випусків продуктів (Х, у), який країна може зробити при заданих технологіях і доступних обсягах ресурсів (х - випуск продукту Х } у - випуск продукту У). Кордон виробничих можливостей - підмножина виробничих можливостей
4. Модель is-lm, історичний контекст, що діють агенти і ринки, історичний контекст і передумови розробки моделі
   В результаті вивчення матеріалу даного розділу студент повинен: знати історичний контекст і передумови розробки моделі IS-LM ; учасників моделі IS-LM і їх ролі; ринки, що входять до складу моделі, і рівняння, що описують рівновагу на окремих ринках; визначення рівноваги в моделі IS-LM, його
5. Моделі національної економіки, критерії класифікації
   В результаті вивчення даного розділу студент повинен: знати - критерії виділення моделей національної економіки; вміти - аналізувати галузеві та регіональні особливості різних моделей національної економіки; володіти - навичками дослідження європейської, американської, азіатської та ісламської
6. Модель глобального рівноваги
   Узагальнимо найпростішу кейнсіанську модель рівноваги на випадок глобальної економіки. Аналогом доходу країни (ВВП) тут служить вектор, що складається з доходів всіх країн, а аналогом граничної схильності до заощадження - матриця, що характеризує норму заощадження в кожній країні і інтенсивність
7. Модель ак і конвергенція
   На відміну від моделі Солоу, де темп економічного зростання заздалегідь відомий, тут він є ендогенної величиною, т. Е. Визначається при аналізі моделі. Нехай чисельність населення (L) незмінна, тоді дохід залежить від обсягу капіталу (К) і ефективності праці (Е ): де b - продуктивність економіки.
8. Міжгалузевий баланс за 2011 г
   (Поточні ціни, млн дол. США за паритетом купівельної спроможності, з округленням до цілих) позначення 1 Сільське і лісове господарства, полювання та рибальство 2 Видобуток корисних копалин 3 Виробництво продуктів харчування 4 Виробництво текстильних виробів 5 Виробництво шкіри та взуття 6