Ефект доходу і ефект заміни по Хиксу

Повернемося знову до вихідного рівноваги. Нехай індивід спочатку вибирає набір (X_t, У_;) В точці (рис. 8.13). В даному випадку рівень добробуту для споживача характеризується кривою байдужості U_v Його вихідне бюджетне обмеження представлено лінією БО_г В результаті зростання ціни одиниці товарах бюджетна лінія повертається уздовж осіХ до рівня В0₂. Споживач змушений скорочувати свої покупки до нового набору (X ,, У₂) в точці Е_г Рівень його добробуту знизився до кривої байдужості U_r

Споживачеві знову пропонується компенсація. Однак тепер додатковий дохід повинен бути таким, щоб рівень добробуту індивіда не змінився, незважаючи на зростання ціни товару X. Як же знайти цей новий дохід?

Для цього ми повинні звернути увагу на двоїсту задачу споживчого вибору. Тут нам потрібно обмеження у вигляді початкового рівня добробуту - рівня корисності U_v Але компенсація не повинна бути надмірною. Новий дохід споживача повинен відповідати мінімуму витрат, які дозволять індивіду при новій ціні одного з товарів (в нашому випадку товари) придбати набір, що приносить споживачеві таку ж корисність, яка була у нього спочатку.

Вирішуємо наступне завдання: min Е (Р_Х, P_Y, U) при U = U_y Новий оптимум споживача досягається в точці Е_у Індивід вибирає набір (Х₃, У₃). Цей набір, як можна помітити, відрізняється кількісно від початкового оптимуму, але приносить споживачеві таку ж корисність. Різниця в бюджетах Б0₂ і Б0₃ становить компенсацію за Хиксу. Слід зазначити, що в силу випук-лости кривої байдужості до початку координат оптимальний набір (Х₃, 7₃) Буде розташований завжди лівіше точки початкового вибору Е_у

Досліджуємо докладніше реакцію споживача на зростання ціни товару в версії Хікса.

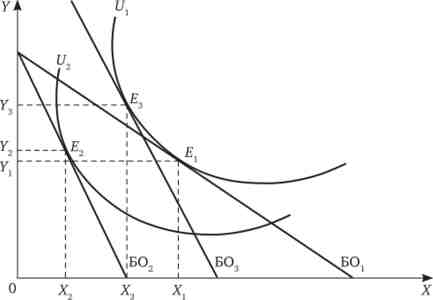
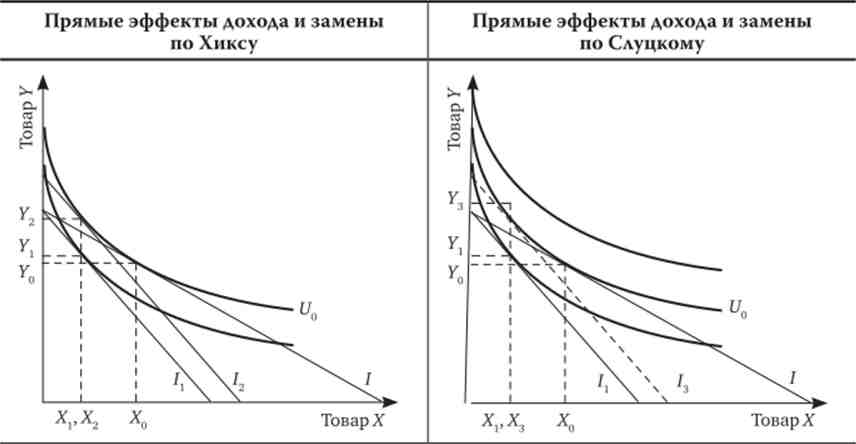
Мал. 8.13. Ефект доходу і ефект заміни по Хиксу

Ефект ціни - різниця в обсягах покупок товарів X і Y (Прямий і перехресний ефекти) між початковим оптимумом і підсумковим вибором Е₂ однакова при однакових змінах цін для одного і того ж споживача і по Хиксу, і по Слуцькому. Ефект заміни по Хиксу визначається переходом індивіда від точки?_J до точки Е₃. Це рух уздовж вихідної кривої байдужості під дією зміни відносних цін товарів і доходу - компенсації споживача. Ефект доходу по Хиксу означає переміщення індивіда з точки?₃ в підсумкову крапку Е₂ - зміна покупок товарів під дією зміни реального доходу споживача.

ШПАРГАЛКА

Як знайти ефекти по Хиксу

?,: Тах1ДХ, У) при БО, (/ ,, Р_х, PJ.

Е₂: MaxU (X, У) при БО_? (/ ,, Р_х, Р_у).

Е₃: min? (P_x, P_v) при l / * = U₁(X_], У,). h ⁼Рх, 'Х + Ру У.

Компенсація за Хиксу: 1₂ - /_|; де /₂ = P_v ? Х₃ + Р_у ? У_:!.

Прямий ефект ціни: ДХ^Р = Х₂-Х_Г Прямий ефект доходу: АХ¹ = Х₂-Х₃.

Прямий ефект заміни: AX^S = Х₃-Х_Г

Перехресний ефект ціни: ДУ '' = У₂ - У ,.

Перехресний ефект доходу: Ay^s = Y₃-Y_r Перехресний ефект заміни: ДУ⁵ = У, - У ,.

Питання для роздумів

Для яких видів переваг ефект заміни завжди дорівнює нулю? Ефект доходу завжди дорівнює нулю? Чому так відбувається?

Теоретичний питання підвищеної складності

Доведіть, використовуючи лему Шепарда, що при невеликих змінах цін різницею між компенсацією за Хиксу і компенсацією за Слуцькому можна знехтувати, т. Е. При невеликих змінах ціни товару компенсація за Хиксу дорівнює компенсації по Слуцькому.

Рішення

Доказ будується на основі леми Шепарда.

Розглянемо повний диференціал функції корисності:

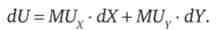
винесемо MU_Y в правій частині виразу за дужку, в результаті отримаємо

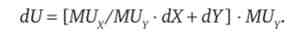
У точці оптимуму споживача має місце рівність

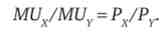
Підставами це рівність в вираз повного диференціала функції корисності

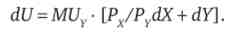
винесемо P_Y в правій частині за дужку і отримаємо

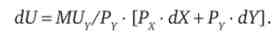
У точці оптимуму споживача діє еквімаржінальний принцип

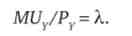
Зміна ціни товару X веде до відносного зміни доходу споживача (ефекту доходу), який можна виразити через повний диференціал функції бюджетного обмеження споживача (функції доходу споживача):

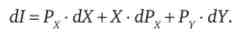
Звідки отримуємо

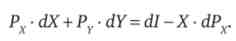
Підставами цей вислів в повний диференціал функції корисності, тоді

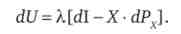
На основі цього виразу ми бачимо, що зміна сукупної корисності в результаті зміни ціни залежить від двох чинників - зміни доходу (d /) і зміни вартості первинного набору (X - dP_x).

Компенсація за Хиксу виходить з того, що рівень корисності не повинен змінитися, т. Е. dU = 0.

При цьому, так як X> 0,

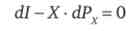
або

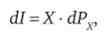
т. е. зміна доходу повинно в точності компенсувати зміну ціни, а це є компенсація за Слуцькому.

Таким чином, при невеликих змінах ціни товару компенсація за Хиксу дорівнює компенсації по Слуцькому.

Отже, ефект ціни може бути розкладений на два самостійних ефекту - ефект доходу і ефект заміни. Ці ефекти можуть бути як прямими, що зачіпають реакцію споживача на зміну ціни даного товару, так і непрямими (перехресними), що показують реакцію індивіда по відношенню до інших товарах в наборі. Оскільки ефект заміни характеризує чисту реакцію споживача на динаміку ціни одного з товарів, т. Е. Реакцію незалежно від впливу ціни на купівельну спроможність його грошей, знак перехресного ефекту заміни класифікує товари X і Y на чисті субститути (знак позитивний), чисті комплементи (знак негативний) і чисті нейтральні товари (ефект дорівнює нулю). Тоді загальний ефект ціни відносно двох товарів буде їх поділяти на загальні субститути (знак перехресного ефекту ціни позитивний), загальні комплементи (знак негативний) і загальні нейтральні товари (ефект дорівнює нулю).

Завдання, що ілюструє теорію

Функція корисності споживача задана як:

• а) U = Х¹¹² -Y^1/2;
• б) U = Х '² +Y.

Ціна одиниці товарах дорівнює 2 руб., Ціна одиниці товару Y становить 4 руб. Споживач виділяє на покупку двох товарів 100 руб.

• 1. Яка кількість товару купить споживач?
• 2. Яким чином зміниться оптимальний набір споживача, якщо ціна товару X зросте в два рази (до 4 руб.)?
• 3. Чому при цьому будуть рівні прямі ефекти доходу і ефект заміни (по Хиксу і по Слуцькому)?
• 4. Чому при цьому будуть рівні перехресні ефекти доходу і за-міни?
• 5. Чи є товари X і Y загальними субститутами або комплементами?
• 6. Чи є товари X і У чистими субститутами або комплементами?

Рішення

1. Знайдемо точку оптимального споживання:

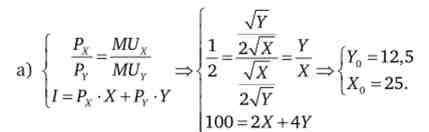
Значення функції корисності в цій точці дорівнює

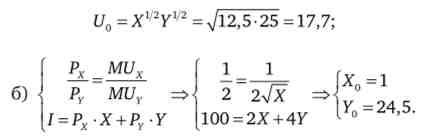
Значення функції корисності в цій точці дорівнює

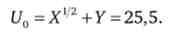
2. Знайдемо нові значення оптимальних обсягів споживання після зміни цін під час відсутності компенсації доходу

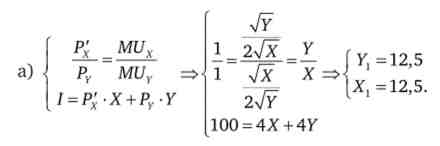
Значення функції корисності в цій точці дорівнює

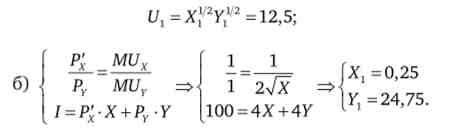
Значення функції корисності в цій точці дорівнює

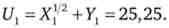
3. Знайдемо прямі ефекти заміни і доходу компенсованого попиту по Слуцькому і по Хиксу. Для зручності аналізу представимо отримані результати в таблицях, а) Для функції корисності виду: U = X '²У¹²

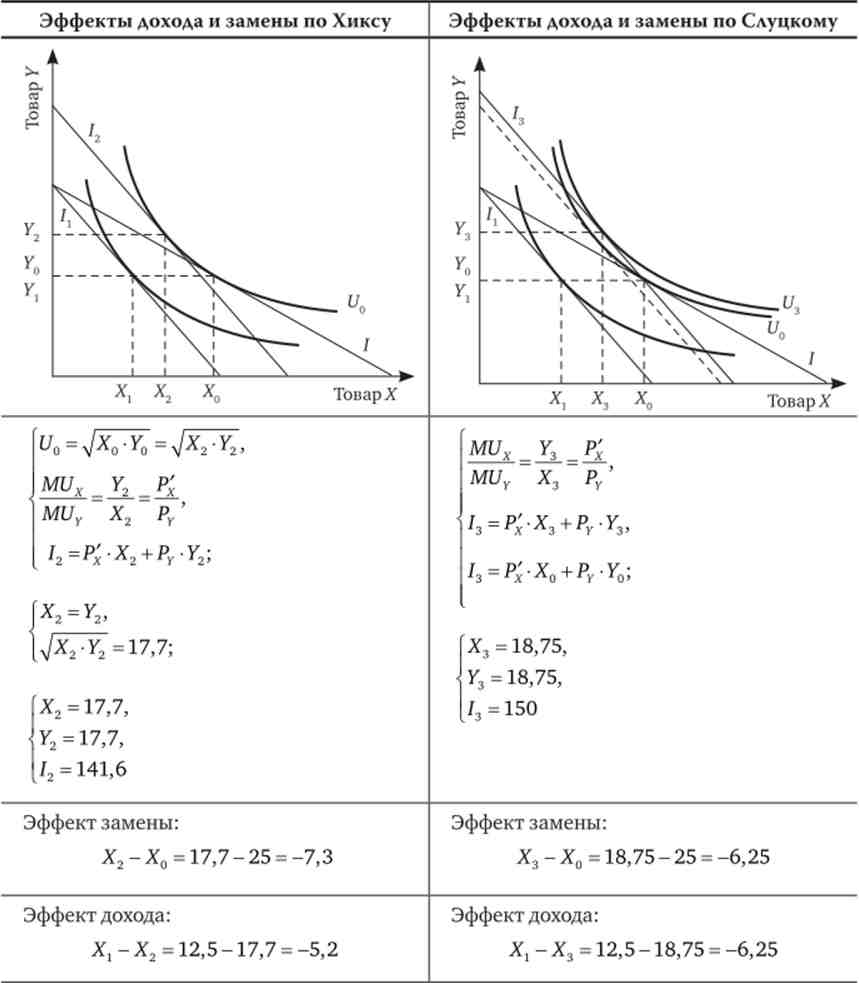
б) Для функції корисності виду: U = X^V2 + У

• 4. Знайдемо перехресні ефекти заміни і доходу компенсованого попиту по Слуцькому і по Хиксу.
• а) Для функції корисності виду: U = X^V2Y^V2

б) Для функції корисності виду: U = X¹² + Y

5. Визначимо знак перехресної еластичності товарів за ціною: а) для функції корисності виду: U = Х^{,/ 2} У¹'²

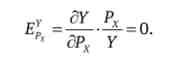
З міркувань симетрії функції корисності можна зробити висновок, що

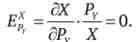
Отже, товари X і У є незалежними (не загальними комплементами і не загальними субститутами, а загальними нейтральними товарами);

б) для функції корисності виду: U = X¹'² + У

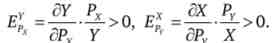
Отже, товари є загальними субститутами. Причому товар X-це товар першої необхідності, так як його споживання після певного рівня доходу перестає залежати від доходу.

6. Для функції корисності виду: U = X¹² - У¹² ефект заміни позитивний, тому товари X і У є чистими субститутами, для функції корисності виду: U = Х¹² +У ефект заміни теж позитивний, хоча набагато менше і практично наближається до нуля. У цьому випадку ми можемо охарактеризувати товари X і У або як незначні чисті субститути, або, швидше за все, як чисті нейтральні товари.

1. Конкурентний ринок із зовнішнім ефектом
   В яких випадках виникає зовнішній ефект економічної діяльності? Зовнішні ефекти виникають тоді, коли ринок виявляється не в змозі за допомогою ціноутворення «втягнути» в процедуру обміну всі вигоди і витрати будь-якої діяльності економічних агентів. Тому зовнішні ефекти можуть розглядатися
2. Компенсує варіація доходу
   Компенсирующая варіація доходу показує величину доходу, на яку треба змінити початковий дохід споживача, щоб при зміні ціни товару його добробут не змінився. Компенсуючу варіацію доходу ми вже розглядали в гл. 8 при дослідженні ефекту доходу. Згадаймо основні положення. Нехай початковий вибір
3. Кількісні обмеження
   Крім використання податків і субсидій для регулювання обсягів зовнішніх ефектів держава може застосовувати заходи прямої заборони або прямого контролю рівня виробництва. У кожній країні, як правило, є стандарти якості навколишнього середовища, які регулюють обсяги негативних зовнішніх ефектів
4. Інші характеристики ризику
   Крім ймовірності результату для характеристики ризику та невизначеності можуть використовуватися показники очікуваної величини і розкиду очікуваної величини. Математичне очікування знаходиться за формулою і характеризує середньозважене значення результатів. Як терезів беруться ймовірності
5. Індекс сіна
   Індекс Сена - вимірювач бідності. Дохід в концепції Сена розглядається не як кінцева мета, а як засіб, що розширює людський вибір мети і того способу життя, які людина вважає кращими. Він показав, що добробут людей має оцінюватися рівнем доходів, а їх можливістю забезпечувати гідне життя в
6. Хвилювання на місцях
   Віктор Дамурчіев на останньому «хозактива» пообіцяв, що в 2007 р департамент з допомогою територіальних органів зареєструє права власності на 8000 земельних ділянок, збільшить обсяг площ міських угідь, офіційно оформивши їх, і буде активніше захищати земельно-майнові інтереси міста в судах.
7. Функція корисності споживача
   Аксіоми раціонального вибору споживача визначають функцио-наль- ву залежність між кількістю споживаного товару і ступенем задоволеності споживача, яка називається функцією корисності. визначення функція корисності показує залежність рівня добробуту споживача (сукупної корисності товарного
8. Фактори, що впливають на попит
   Закон попиту показує залежність між ціною товару і обсягом його покупки. Але на споживача, як уже зазначалося вище, впливають і інші фактори. Як же їх включити в наш аналіз? Будь-які інші чинники, які можуть вплинути на попит, викликають зміна всієї лінії попиту при будь-яку ціну одиниці товару.