Адаптивні очікування в моделі AD-AS

Ми почнемо з розгляду випадку так званих адаптивних очікувань. Це, мабуть, найбільш давно використовується економістами тип очікувань, які досить просто моделювати.

Формально термін «адаптивні» стосовно очікуванням був, мабуть, вперше використаний в роботі Кеннета Ерроу та Марка Нерлова в 1958 р *, хоча моделі, що описують таке явище, почали з'являтися в середині 1950-х рр. в роботах різних авторів (див., наприклад роботу М. Фрідмана 1957 р приводу функції споживання або роботу Філіпа Кейган 1956 р але гіперінфляції). Такий тип очікувань використовувався для дослідження питання про стабільність динамічного процесу «намацування» в так званій паутинообразной моделі - моделі, яка описувала процес встановлення рівноважної ціни в результаті підстроювання попиту і пропозиції на окремо взятому ринку.

В основі адаптивних очікувань лежить припущення про те, що економічні агенти формують свої прогнози щодо майбутніх значень економічних змінних, орієнтуючись на їхні минулі значення і на те, наскільки їхні власні попередні прогнози були помилкові. Зрозуміло, такі очікування характерні тільки для досить стабільних періодів. Нижче ми розглянемо, як можуть розгортатися події в моделі AD-AS в разі адаптивних очікувань з приводу рівня цін і з приводу рівня інфляції.

Перш ніж перейти до власне розгляду моделі з очікуваннями, зробимо кілька спрощують припущень. Нагадаємо, що розглянуті нами моделі сукупної пропозиції в деякому середньостроковому періоді дозволяють описати функцію сукупної пропозиції як Y^s = Y^S(P / Р^е), причому У '(-) - монотонно зростаюча функція. Слід зазначити, що в разі точного прогнозу (Р / Р^е = 1) випуск дорівнює природному рівню Y.

Для аналізу взаємодії сукупного попиту та сукупної пропозиції зручно переписати функції AD і Лб 'в логарифмічних змінних, які ми будемо позначати за допомогою малих літер. Більш того, ми спростимо задачу, припускаючи, що функція сукупної пропозиції лінійна в цих змінних, т. Е.

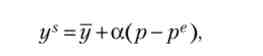
де y^s = lnF^s, у = In У, р = InP, р^е = LnP '', а 0.

Що стосується сукупного попиту, то для наших цілей достатньо вважати, що він випливає з рівності Y '¹ = MV / Р, причому ми можемо, не применшуючи спільності, вважати, що V = 1. Іншими словами, ми будемо припускати, що

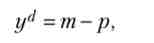
де y^d = Y^d, т = пМ. Ми обмежуємося лише цієї найпростішою формою сукупного попиту, оскільки в моделі AD-AS майже неважливо, зсувається крива AD за допомогою зміни параметрів фіскальної політики або ж грошово-кредитної. Для розгляду очікувань нам досить вважати, що в нашому розпорядженні є тільки один параметр - грошова маса М, або, точніше, т. Ми будемо розглядати взаємодію сукупного попиту і пропозиції в дискретному часі, і наша модель буде записуватися наступним чином:

Остання рівність означає, що рівень випуску визначається рівністю сукупного попиту і сукупної пропозиції, т. Е. Мова йде про рівновагу в моделі AD-AS (Рис. 13.1).

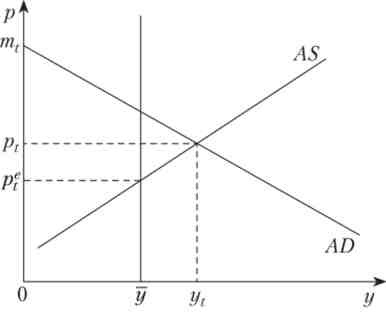
Мал. 13.1. Рівновага в моделі AD-AS

Виписану вище модель можна переписати в більш простому вигляді:

1. Діяльність держави на мікрорівні
   Дослідження загальної рівноваги в національній економіці призводить до розуміння таких явищ, які ведуть до збоїв в роботі ринкового механізму, нездатності конкурентного ринку самого по собі забезпечити економічну ефективність. Згідно з традицією А. Сміта і класичної школи, якщо немає яких-небудь
2. Дискусію щодо використання асиметрій в макроекономічному аналізі
   У 1980-х і в першій половині 1990-х рр. в економічній науці розгорнулася дискусія про можливість залучення питань асиметрії в макроекономіку з метою підвищення достовірності економетричних вимірювань бізнес-циклів. З цією метою була встановлена залежність часу і темпів фази відновлення та
3. Динаміка світових цін
   Головне питання, яке постає перед будь-якою фірмою, що має справу з міжнародним сектором економіки, - які будуть світові ціни в найближчому майбутньому? Хоча точне прогнозування - справа дуже і дуже складне, деякі ключові моменти динаміки цін можна виявити на основі аналізу світового попиту
4. Динаміка економічного циклу
   Починаючи від Адама Сміта економісти намагалися розгадати головоломки економічного зростання і економічної рівноваги. Стандартні моделі економічного зростання засновані на припущеннях спадної віддачі на капітал з технологічних інновацій або на ендогенної динаміці в поєднанні з відповідною
5. Динамічна функція сукупної пропозиції, відсутність інфляційних очікувань
   У пункті 7.4 було показано, що обсяг сукупної пропозиції при заданій технології виробництва залежить від поведінки підприємців і домашніх господарств на ринку праці. При цьому специфіка поведінки домашніх господарств полягає в тому, що в разі підвищення рівня цін ціна пропозиції праці (W
6. Держава, поняття і цілі грошово-кредитної політики держави
   Третій важливий агент, зазвичай присутній в макроекономічних моделях, - держава. Воно розглядається в макроекономіці зазвичай як єдине ціле, без поділу на уряд і ЦБ. Передбачається, що держава діє в цілях збільшення суспільного добробуту, використовуючи інструменти фіскальної та грошово-кредитної
7. Бюджетне обмеження домашніх господарств. Умова Понці
   Бюджетне обмеження домогосподарств - теперішня вартість споживання (С) не повинна перевищувати суми початкового багатства / С (0) і дисконтованого доходу (W): Запишемо дисконтну вартість заощаджень W-С, використовуючи метод інтегрального дисконтування, описаний в підпункті 1.3.3: У момент
8. Баланс трудових ресурсів і його прогноз
   Баланс трудових ресурсів - система показників, яка відображає наявність трудових ресурсів і їх розподіл за сферами та видами діяльності. Складається щорічно по країні в цілому, республікам у складі Російської Федерації, краях і областях з розподілом на міську та сільську місцевості. Баланс