5.4. Детерминированное моделювання та перетворення факторних систем
Одним із завдань факторного аналізу є моделювання взаємозв'язків між результативними показниками і факторами, які визначають їх величину.
Моделювання - це один з найважливіших методів наукового пізнання, за допомогою якого створюється модель (умовний образ) об'єкта дослідження. Сутність його полягає в тому, що взаємозв'язок досліджуваного показника з факторними передається у формі конкретного математичного рівняння.
У факторному аналізі розрізняють моделі детерміновані (функціональні) і стохастичні (кореляційні). За допомогою детермінованих факторних моделей досліджується функціональний зв'язок між результативним показником (функцією) і факторами (аргументами).
При моделюванні детермінованих факторних систем необхідно виконувати ряд вимог.
1. Фактори, що включаються в модель, і самі моделі повинні мати виразно виражений характер, реально існувати, а не бути придуманими абстрактними величинами або явищами.
2. Фактори, які входять в систему, повинні бути не тільки необхідними елементами формули, але і знаходитися в причинно-наслідкового зв'язку з досліджуваними показниками. Інакше кажучи, побудована факторна система повинна мати пізнавальну цінність. Факторні моделі, які відображають причинно-наслідкові відносини між показниками, мають значно більше пізнавальне значення, ніж моделі, створені за допомогою прийомів математичної абстракції. Останнє можна проілюструвати наступним чином. Візьмемо дві моделі:
1) ВП=ЧРхГВ:
2) ГВ=ВП / ЧР, де ВП - валова продукція підприємства; ЧР - чисельність працівників на підприємстві; ГВ - середньорічна вироблення продукції одним працівником.
У першій системі фактори знаходяться в причинному зв'язку з результативним показником, а в другій - в математичному співвідношенні. Значить, друга модель, побудована на математичних залежностях, має менше пізнавальне значення, ніж перша.
3. Всі показники факторної моделі повинні бути кількісно вимірними, тобто повинні мати одиницю виміру і необхідну інформаційну забезпеченість.
4. Факторна модель повинна забезпечувати можливість вимірювання впливу окремих факторів, це означає, що в ній повинна враховуватися домірність змін результативного і факторних показників, а сума впливу окремих факторів повинна дорівнювати загальному приросту результативного показника.
У детермінованому аналізі виділяють наступні типи найбільш часто зустрічаються факторних моделей.
1. Адитивні моделі:
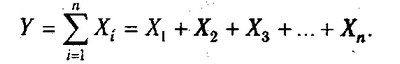
Вони використовуються в тих випадках, коли результативний показник являє собою алгебраїчну суму декількох факторних показників.
2. Мультиплікативні моделі:
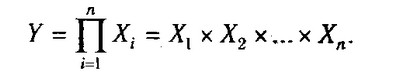
Цей тип моделей застосовується тоді, коли результативний показник являє собою твір декількох факторів.
3. Кратні моделі:
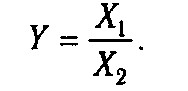
Вони застосовуються тоді, коли результативний показник отримують діленням одного факторного показника на величину іншого.
4. Змішані (комбіновані) моделі - це поєднання в різних комбінаціях попередніх моделей:
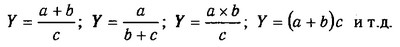
Моделювання мультиплікативних факторних систем в АХД здійснюється шляхом послідовного розчленування факторів вихідної системи на фактори-співмножники. Наприклад, при дослідженні процесу формування обсягу виробництва продукції (див. рис. 5.2) можна застосовувати такі детерміновані моделі, як:
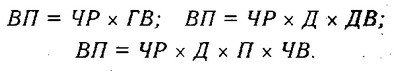
Ці моделі відображають процес деталізації вихідної факторної системи мультиплікативного виду і розширення її за рахунок розчленування на сомножители комплексних факторів.
Аналогічним чином здійснюється моделювання адитивних факторних систем за рахунок розчленування одного або декількох факторних показників на складові елементи.
Як відомо, обсяг реалізації продукції дорівнює:
VРП=VBП - Vи,
де VBП - обсяг виробництва; Vи - обсяг внутрішньогосподарського використання продукції.
У господарстві продукція використовувалася як насіння (С) та кормів (К). Тоді наведену вихідну модель можна записати наступним чином: V РП=VBП - (С + К).
До класу кратних моделей застосовують такі способи їх перетворення: подовження, формального розкладання, розширення та скорочення.
Перший метод передбачає подовження чисельника вихідної моделі шляхом заміни одного або декількох факторів на суму однорідних показників. Наприклад, собівартість одиниці продукції можна представити як функції двох факторів: зміни суми витрат (3) і обсягу випуску продукції (VBП). Вихідна модель цієї факторної системи буде мати вигляд
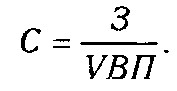
Якщо загальну суму витрат (3) замінити окремими їх елементами, такими, як заробітна плата (3П), сировину і матеріали (СМ), амортизація основних засобів (А), накладні витрати (HP) та ін, то детермінована факторна модель буде мати вигляд адитивної моделі з новим набором факторів:
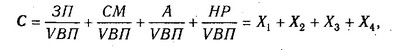
де Х1 - трудомісткість продукції; Х2 - матеріаломісткість продукції; Х3 - фондомісткість продукції; Х4 - рівень накладних витрат.
Спосіб формального розкладання факторної системи передбачає подовження знаменника вихідної факторної моделі шляхом заміни одного або декількох факторів на суму або твір однорідних показників. Якщо В=L + М + N + Р, то
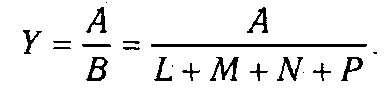
В результаті, отримали кінцеву модель того ж виду, що й вихідної факторної системи (кратну модель). На практиці таке розкладання зустрічається досить часто. Наприклад, при аналізі показника рентабельності виробництва (R):
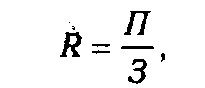
де П - сума прибутку від реалізації продукції; 3 - сума витрат на виробництво і реалізацію продукції. Якщо суму витрат замінити на окремі її елементи, кінцева модель в результаті перетворення придбає наступний вигляд:
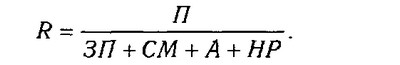
Собівартість одного тонно-кілометра залежить від суми витрат на утримання та експлуатацію автомобіля (3) і від його середньорічний вироблення (ГВ). Вихідна модель цієї системи буде мати вигляд: Сткм=3 / ГВ. Враховуючи, що середньорічна вироблення машини в свою чергу залежить від кількості відпрацьованих днів одним автомобілем за рік (Д), тривалості зміни (П) і середньогодинної вироблення (ЧВ), ми можемо значно подовжити цю модель і розкласти приріст собівартості на більшу кількість факторів:
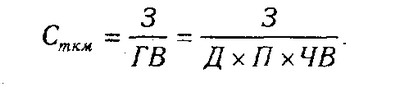
Метод розширення передбачає розширення вихідної факторної моделі за рахунок множення чисельника і знаменника дробу на один або кілька нових показників. Наприклад, якщо у вихідну модель
Y=A / B
ввести новий показник з, то модель прийме вигляд
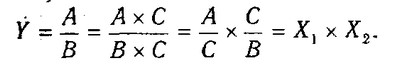
В результаті вийшла кінцева мультиплікативна модель у вигляді твору нового набору факторів.
Цей спосіб моделювання дуже широко застосовується в аналізі. Наприклад, середньорічну вироблення продукції одним працівником (показник продуктивності праці) можна записати таким чином: ГВ=ВП / ЧР.
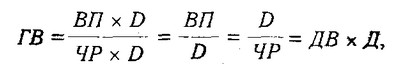
де ДВ - середньоденна вироблення; Д - кількість відпрацьованих днів одним працівником.
Після введення показника кількості відпрацьованих годин усіма працівниками (Г) отримаємо модель з новим набором факторів: середньогодинної вироблення (ЧВ), кількості відпрацьованих днів одним працівником (Д) і тривалості робочого дня (Я):
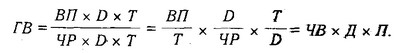
Спосіб скорочення являє собою створення нової факторної моделі шляхом ділення чисельника і знаменника дробу на один і той же показник:
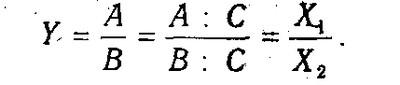
У даному випадку виходить кінцева модель того ж типу, що й вихідна, однак з іншим набором факторів.
І знову практичний приклад. Як відомо, економічна рентабельність роботи підприємства розраховується діленням суми прибутку (П) на середньорічну вартість основного і оборотного капіталу підприємства (KL):
R=П / KL.
Якщо чисельник і знаменник поділимо на обсяг реалізації продукції (товарообіг), то отримаємо кратну модель, але з новим набором факторів: рентабельності продажів і капіталомісткості продукції:

І ще один приклад. Фондовіддача (ФО) визначається відношенням валової (ВП) або товарної продукції (ТП) до середньорічної вартості основних виробничих фондів (ОПФ):
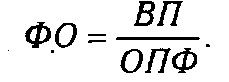
Розділивши чисельник і знаменник на середньорічну кількість робітників (ЧР), отримаємо більш змістовну кратну модель з іншими факторними показниками: середньорічний вироблення продукції одним робітником (ГВ), що характеризує рівень продуктивності праці, і фондоозброєності праці (Фв):
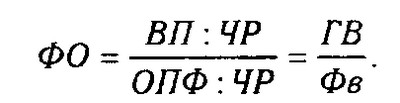
Необхідно зауважити, що на практиці для перетворення однієї і тієї ж моделі може бути послідовно використано кілька методів. Наприклад:
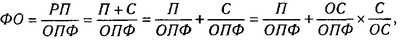
де ФО - фондовіддача; РП - обсяг реалізованої продукції (виручка); С - собівартість реалізованої продукції; П - прибуток; ОПФ-середньорічна вартість основних виробничих фондів; ОС - середні залишки оборотних коштів.
У цьому випадку для перетворення вихідної факторної моделі, яка побудована на математичних залежностях, використані способи подовження і розширення. У результаті вийшла більш змістовна модель, яка має велику пізнавальну цінність, тому що враховує причинно-наслідкові зв'язки між показниками. Отримана кінцева модель дозволяє дослідити, як впливають на фондовіддачу рентабельність основних засобів виробництва, співвідношення між основними і оборотними засобами, а також коефіцієнт оборотності оборотних коштів.
Таким чином, результативні показники можуть бути розкладені на складові елементи (фактори) різними способами і представлені у вигляді різних типів детермінованих моделей. Вибір способу моделювання залежить від об'єкта дослідження, поставленої мети, а також від професійних знань і навичок дослідника.
Процес моделювання факторних систем - дуже складний і відповідальний момент в АХД. Від того, наскільки реально і точно створені моделі відображають зв'язок між досліджуваними показниками, залежать кінцеві результати аналізу.
Інформація, релевантна " 5.4. Детерминированное моделювання та перетворення факторних систем "
- 2.2.2. Види зв'язків в економічних системах
детермінованою), якщо будь-якому значенню факторної ознаки відповідає цілком визначене невипадкове значення ознаки результативного. Система називається жорстко детермінованої, якщо за даних початкових умов вона переходить в єдино можливе (зовсім визначене) стан. Аналіз жорстко детермінованих систем часто називають факторним аналізом. Детально він буде розглянутий - 2.5.6. Методи ситуаційного аналізу та прогнозування
детермінованих зв'язків, коли кожному значенню факторної ознаки відповідає цілком визначене невипадкове значення результативної ознаки. Як приклад можна привести залежності, реалізовані в рамках відомої моделі факторного аналізу фірми "Дюпон" (ця модель буде розглянута в розділі 4.8). Використовуючи цю модель і підставляючи в неї прогнозні значення різних факторів, - 1.3. Предмет і основні методи аналізу господарської діяльності бюджетних організацій
детерміновані зв'язку, друга - стохастичні. Характерною особливістю детермінованих (функціональних) зв'язків є те, що зміни фактора на одиницю свого значення завжди відповідає зміна результативного показника на строго певну величину. Виділяють наступні види таких причинно-наслідкових залежностей: - аддитивная залежність - результативний показник (РП) - 5.1. Поняття, типи та завдання факторного аналізу
детермінований і стохастичний; прямий і зворотний; одноступінчатий і багатоступінчастий; статичний і динамічний; ретроспективний і перспективний (прогнозний). Детермінований факторний аналіз являє собою методику дослідження впливу чинників, зв'язок яких з результативним показником носить функціональний характер, тобто коли результативний показник представлений у вигляді - 2.6.2. Факторний аналіз на основі жорстко детермінованих моделей
детермінований факторний аналіз, тобто аналіз залежностей між показниками за допомогою жорстко детермінованих факторних моделей. Основним результатом детермінованого факторного аналізу є розкладання приросту результативного показника, обумовленого спільним впливом або зміною факторних ознак, на суму приватних приростів результативного показника, будь-який з яких - 2.2.1. Моделювання та аналіз факторних систем
моделювання економічного явища. Економічні моделі можуть мати різну математичну форму. Зв'язок між факторами може бути одного з наступних типів. Аддитивная зв'язок. Результуючий фактор визначається сумою факторів залежних, можливо, з деякими коефіцієнтами пропорційності. Зв'язок описується наступною формулою: {foto14} Прикладом такого зв'язку може бути довжина - 5.3. Систематизація факторів в аналізі господарської діяльності
детерминированном і стохастичному аналізі. Системний підхід в АХД викликає необхідність взаємопов'язаного вивчення факторів з урахуванням їх внутрішніх і зовнішніх зв'язків, взаємодії і співпідпорядкованості, що досягається за допомогою систематизації. Систематизація в цілому - це розміщення досліджуваних явищ або об'єктів у певному порядку з виявленням їх взаємозв'язку і підпорядкованості. Одним з - Логарифмічний метод
детермінованого факторного аналізу є оцінку впливу відносної зміни факторів на відносне зміна результативного показника, тобто визначення ставлення величини приросту, викликаного зміною будь-якого фактора, до величини результативного показника за базисний період у відсотках. Вона вирішується за допомогою індексного методу і буде розглянута в розділі 2.7.4. - 2.8.1. Кореляційний аналіз
детермінованою обернено пропорційній зв'язку між факторами, r=+1 відповідає жорстко детермінованої зв'язку з прямо пропорційною залежністю факторів. Якщо лінійного зв'язку між факторами не спостерігається, r 0. Інші значення коефіцієнта кореляції свідчать про наявність стохастичною зв'язку, причому чим ближче | r | до одиниці, тим зв'язок тісніше. При | r | 0,7 - тісний. Існують і - Неокласичний напрям
моделювання рівноваги дозволяє знайти відхилення реальних процесів від ідеалу. Найбільш відомі факторна модель Кобба-Дугласа і проста односекторная модель економічної динаміки Р. Солоу. Факторна модель Кобба-Дугласа (див. 2.2) показує взаємодію і взаємозамінність праці і капіталу, наскільки продукт зобов'язаний своїм створенням тому чи іншому чиннику, при якій їх комбінації може - 6.3. Спосіб абсолютних різниць
детерминированном аналізі, але тільки в мультиплікативних і мультиплікативно-адитивних моделях: Y=(а - b) с і У=a (b - с). І хоча його використання обмежене, але завдяки своїй простоті він отримав широке застосування в АХД. Особливо ефективно застосовується цей спосіб у тому випадку, якщо вихідні дані вже містять абсолютні відхилення по факторним показниками. При його використанні величина - Валовий національний продукт
факторних (первинних) доходів, експорту та імпорту (чистий експорт) і поточних трансфертів, отриманих з-за кордону, тобто: Sрасч=Sф.д. + Sекс-імп + Sтр, де Sф.д - сальдо факторних доходів; Sекс-імп - сальдо експорту та імпорту, або чистий експорт; Sтр - сальдо поточних трансфертів. Якщо сальдо експорту та імпорту є складовою частиною і ВВП, і ВНП, то сальдо поточних трансфертів не має ніякого - 6.7. Спосіб логарифмування в аналізі господарської діяльності
детермінованого факторного аналізу та сферу їх застосування, результати можна систематизувати у вигляді такої матриці: {foto108} Знання сутності даних прийомів, області їх застосування, процедури розрахунків - необхідна умова кваліфікованого проведення кількісних - 2.8. Математико-статистичні методи вивчення зв'язків
детермінованого аналізу. В аналізі фінансово-господарської діяльності стохастичні моделі використовуються, коли необхідно: оцінити вплив факторів, по яких не можна побудувати жорстко детерміновану модель; вивчити і порівняти вплив факторів, які неможливо включити в одну і ту ж детерміновану модель; виділити і оцінити вплив складних факторів, які не можуть бути - Види факторних доходів
факторними доходами. Власники факторів виробництва (економічних ресурсів) отримують такі види доходів: від природних ресурсів - ренту (земельну, гірську, плату за воду і т.д.); від трудових ресурсів - заробітну плату; від капіталу - відсоток (як дохід власників грошового капіталу) і прибуток (як дохід власників реального капіталу); від підприємницьких здібностей - - 15. МЕТОДИ факторний аналіз ЕКОНОМІЧНИХ ПОКАЗНИКІВ
детерминированном аналізі для цього використовуються наступні способи. Найбільш універсальним з них є спосіб ланцюгової підстановки; він використовується для визначення кількісного впливу окремих факторів на загальний результативний показник. Даний спосіб застосовується в тому випадку, якщо між досліджуваними явищами існує функціональна, пряма або обернено пропорційна залежність. При - Імітаційне моделювання
детермінованою факторної моделі, що пов'язує результативну ознаку (прибуток) з факторами (доход від реалізації, рівень витрат, рівень податкових ставок і ін.) Один з можливих підходів прогнозування в цьому випадку може виглядати наступним чином. Ставиться завдання виявлення і дослідження факторів розвитку господарюючого суб'єкта і встановлення ступеня їх впливу на різні результатні - Г. В. Савицька. Аналіз господарської діяльності підприємства. 4-е видання, перероблене і доповнене, 2001
- 7.1. Поняття стохастичною зв'язку і завдання кореляційного аналізу
детермінованого факторного аналізу. Однак на практиці далеко не всі економічні явища і процеси можуть вивчатися за допомогою цієї методики, так як в більшості випадків їх не можна звести до функціональних залежностях, коли величиною факторного показника відповідає єдина величина результативного показника. Частіше в економічних дослідженнях зустрічаються стохастичні