| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Підприємець реалізує проект, який частково фінансується зовнішнім інвестором. Виражений в рублях випуск проекту q є випадковою величиною, рівномірно розподіленим на інтервалі [0, Q], Успішний проект - випуск виявився більше величини, яку підприємець повинен інвестору. Згідно з контрактом підприємець виплачує інвестору фіксовану суму Д якщо проект успішний і q > D. Він віддає йому весь випуск, якщо проект не успішний і q < D, при цьому інвестор несе витрати особливого виду.
Витрати верифікації випуску (с) - витрати фірми, пов'язані з необхідністю отримати достовірну оцінку випуску іншої фірми, їх величина характеризує ступінь асиметрії інформації.
Чистий дохід інвестора (R) - очікувана величина його доходу без урахування витрат верифікації випуску. Отримаємо формулу чистого доходу, для цього розглянемо два випадки:
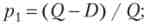
- відрізок [0, D] відповідає безлічі неуспішних проектів (q < D), а ймовірність невдачі проекту дорівнює відношенню довжин відрізків:
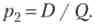
Чистий дохід інвестора в разі успіху проекту дорівнює обумовленій сумі боргу Д В разі невдачі він дорівнює середньому значенню випуску на відрізку [О, D] за вирахуванням витрат верифікації, м. тобто дорівнює різниці D / 2 і с. Отже, очікуваний чистий дохід дорівнює
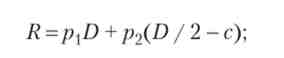
- якщо D> Q, то проект свідомо неуспешен, і інвестор отримує очікуваний випуск за вирахуванням витрат верифікації: R0 = Q / 2 - с.
Рівновага інвестора - очікуваний чистий дохід інвестора максимальний. Підставами ймовірності успіху і неуспіху
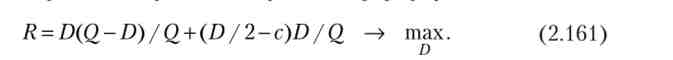в формулу чистого доходу:
Умова рівноваги інвестора отримаємо, прирівнявши нулю похідну цільової функції (2.161) по змінній D:
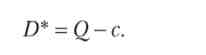
Отже, без урахування фактора прибутковості оптимальна для інвестора величина виплати дорівнює різниці максимального випуску і витрат верифікації, при цьому максимальний чистий дохід дорівнює
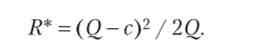
Нехай проект вимагає вкладень W{) одиниць ресурсу, при цьому підприємець вкладає W, а інвестор вкладає 1Т0 - W. Необхідна норма прибутковості інвестора (ставка відсотка) дорівнює г, тоді необхідний чистий дохід інвестора дорівнює R, = (W0 - 110 (1 + г) -
Необхідну величину виплат інвестору (D) Знайдемо, прирівнявши значення Rt цільової функції інвестора (2.161), одержимо квадратне рівняння:
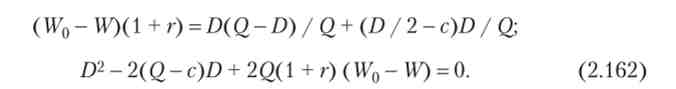
Дискримінант рівняння (2.162) дорівнює
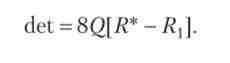
Звідси випливає:
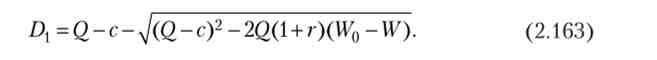
Тепер розглянемо поведінку підприємця в ситуації, коли інвестор визначив оптимальну для себе величину виплати Z) j. Підприємець буде інвестувати в проект свою частину W, якщо чистий дохід від проекту більше доходу від інвестицій в безризиковий актив (1 + г) IT. При оптимістичному прогнозі його очікуваний чистий дохід дорівнює максимальному випуску (()) за вирахуванням мінімального доходу інвестора (1 + г) (Wo - W) і очікуваних витрат верифікації (с). Останні пропорційні ймовірності p '2= Dl / Q невдачі проекту застосовується для розрахунку виплати (q < D,):
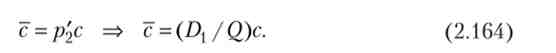
З (2.163) і (2.164) слід ', що величина з убуває з ростом W і дорівнює нулю при W = U '0. Отже, умова участі підприємця у проекті:
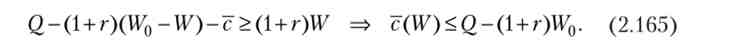
З рівності (2.165) знайдемо частку інвестицій підприємця, починаючи з якої йому вигідна реалізація проекту. Отже, проект буде реалізований, якщо він вигідний обом сторонам, т. Е. Виконуються умови участі в проекті підприємця та інвестора:
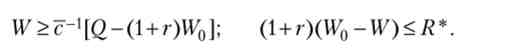
З (2.163) випливає, що максимальну виплату (Q- с) інвестор отримає, якщо його частка дорівнює
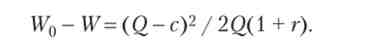
приклад
Визначимо, чи реалізується проект, якщо Q = 10; з = 0,5; W0 = 8; W = 6; г = 0,1. Згідно (2.163) маємо: D = 2,7, прибутковість інвестора: 2,7: 2 - 1 = 0,35 (35%). Згідно (2.164) очікувані витрати верифікації рівні 2,7 - 0,5: 10 = 0,135. Згідно (2.165) дохід підприємця дорівнює 10 - 1,1 - 2 - 0,135 = 7,665, його прибутковість дорівнює 7,665: 6 - 1 = 0,28 (28%). Проект реалізується, так як для обох сторін прибутковість перевищує 10%.