стаціонарні стану

Один з перших питань, на які повинна відповідати та чи інша модель економічного зростання, полягає в тому, як випущений продукт Y_t розподіляється між споживанням C_t і інвестиціями (рівними заощадженням) I_t. Відповідь залежить від того, які міжчасового переваги суспільства в цілому, т. Е. Від того, як суспільство порівнює своє поточне і майбутнє споживання, оскільки, як можна сподіватися, що більше сьогоднішні інвестиції, тим вище буде рівень споживання в майбутньому. Можна припускати, що чим більше суспільство «короткозоро», тим більша частка національного продукту буде витрачатися на поточне споживання (це припущення в явному вигляді фігурує в моделі Рамсея, см. Гл. 20).

Модель Солоу заснована на найпростішому припущенні про те, що розподіл випуску на споживання і валові інвестиції здійснюється за допомогою заданої ззовні і не змінюється з плином часу норми заощадження (норми накопичення) 5 (0<5<1). Тому поряд з співвідношеннями (19.1) - (19.4) для всіх t = 0,1, ..., виконується співвідношення

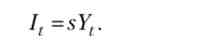
Тепер (19.3) можна переписати в наступному вигляді:

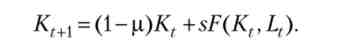
Розділивши останнє рівність на L_tM і взявши до уваги (19.4), ми отримуємо основне рівняння, що задає динаміку в моделі Солоу:

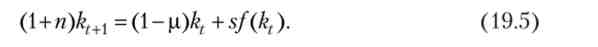
Єдиною залежною змінною в цьому рівнянні є капиталовооруженность праці к. По заданому початковому значенню капиталовооруженности k_d рівняння (19.5) однозначно визначає всю послідовність (k_t)_{t = 0 {} . У свою чергу, знаючи послідовність КАПИТАЛОВООРУЖЕННОСТЬ, ми можемо однозначним чином вказати значення випуску на душу населення, у_з = Y_t / L_t = F (k_t), і споживання на душу населення, c_t = C_r / L, = (1 -s) f (k_t), в будь-який момент часу. Проте, нам буде зручно розуміти під траєкторією в моделі Солоу (що виходить із початкового стану до₀) послідовність КАПИТАЛОВООРУЖЕННОСТЬ і питомих потреблений, (k_f, c_t)_{t = 0 t} .

Тим самим для аналізу поведінки моделі в часі, необхідно досліджувати рівняння (19.5). Перш за все, відповімо на запитання, чи є в моделі стаціонарний стан, т. Е. Така траєкторія (K *_t, c_t)_{t = 0},i, ...> на якій значення капиталовооруженности і споживання на душу населення не змінюються з плином часу (K * = kl ~ k = ... = k *_t = ...; з = Cg =

= q = - = c_t = ...) -

Оскільки за визначенням в стаціонарному стані k *_{t + {} = Kj, то з (19.5) отримуємо, що стаціонарне значення капиталовооруженности до * є рішенням рівняння

значення до * = 0, очевидно, задовольняє рівності (19.6), але змістовного інтересу не представляє, так що ми зосередимося на позитивному вирішенні рівняння (19.6). Відзначимо, що позитивне рішення рівняння (19.6) завжди існує. Необхідна і достатня умова для цього, / '(0)> | Л + п, виконується в силу умов Инада для виробничої функції в інтенсивній формі: Нш / '(^) = °° - Графічно

до-> 0

стаціонарна капиталовооруженность є перетин кривої sf (к), яка б показала частку випуску, яка йде на інвестиції при кожному значенні капиталовооруженности до, і прямий (X + n) k, нахил якої визначається нормою амортизації капіталу і темпом приросту робочої сили (рис. 19.2).

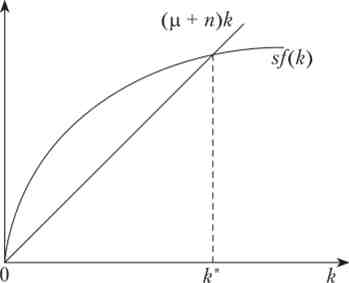
Мал. 19.2. Стаціонарна капиталовооруженность в моделі Солоу

Неважко бачити, що для будь-якої траєкторії (K,, с,), _{= 0} | в моделі Солоу, що виходить із> 0, послідовність КАПИТАЛОВООРУЖЕННОСТЬ монотонно прагне з плином часу до стаціонарного значення, k_t -> до *. Ця збіжність проілюстрована па рис. 19.3.

t -»° о

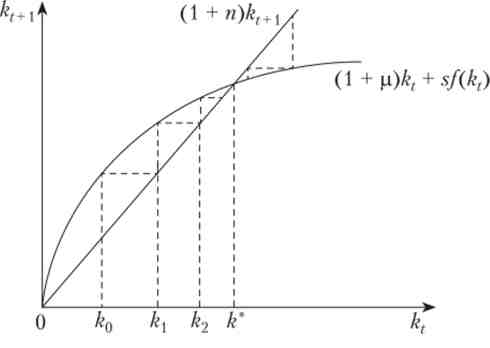
Мал. 19.3. Збіжність в моделі Солоу

З цієї збіжності слід, що випуск на душу населення y_t = f (k_t) сходиться до свого стаціонарного значення / (&*), А споживання на душу населення, з₍ = (1 -s) f (k_t), сходиться до стаціонарного значення з * = (1 -s) f (k *). Таким чином, питомі величини стабілізуються з плином часу. Якщо ж подивитися на валові величини (запас капіталу K_v випуск Y_t, і сукупне споживання C_t), то з збіжності k_t -> K * випливає, що вони

t-> ° о

з плином часу починають рости постійним темпом, що збігається з екзогенно заданим темпом зростання робочої сили:

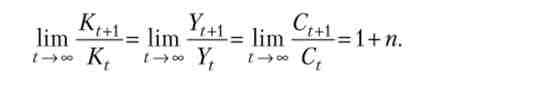
Дійсно, наприклад,

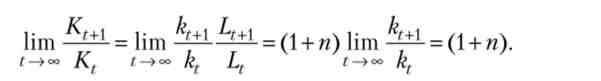
Тим самим будь-яка зміна параметрів моделі не може вплинути на сталість питомих величин в довгостроковому періоді. Це означає, що модель Солоу без технічного прогресу не пояснює, звідки в довгостроковому періоді виникає зростання на душу населення. Зате така модель дає відповідь на питання, чи можна за відсутності технічного прогресу досягти постійного зростання економіки на душу населення шляхом заощадження та інвестування в капітал, накопичуючи більше капіталу на одного робітника. Виявляється, це неможливо - навіть при близькому до одиниці (т. Е. Граничному значенню) нормі заощадження, випуск на душу населення в довгостроковій перспективі в будь-якому випадку буде постійним. Цей факт є прямим наслідком зменшується віддачі на капітал у виробничій функції.

Так що зміни норми заощадження, темпу приросту робочої сили, норми амортизації або параметрів виробничої функції можуть впливати тільки на рівні питомих змінних в стаціонарному стані. Розглянемо, наприклад, як вплине на стаціонарну капиталовооруженность зростання норми заощадження. При збільшенні норми заощадження від ^ до s₂, та частка виробленого продукту, яка інвестується в капітал, зростає, крива sf (k) зсувається вгору, і перетинає пряму ([+ N) k в точці, що відповідає більшому значенню капиталовооруженности. Таким чином, економіка зсувається зі старого стаціонарного стану. У процесі переходу випуск на душу населення буде зростати, але в довгостроковому періоді економіка все одно зійдеться до нового стаціонарного стану (рис. 19.4). Капиталовооруженность в новому стаціонарному стані вище, ніж в старому, що забезпечує більш високі випуск і споживання на душу населення.

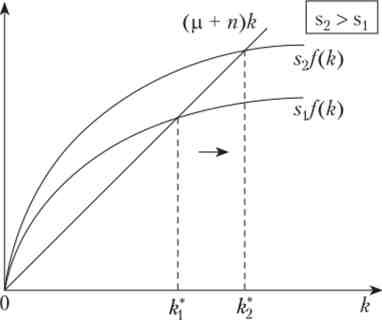
Мал. 19.4. Модель Солоу: збільшення норми заощадження

Можна також дослідити питання, що станеться зі стаціонарної КАПИТАЛОВООРУЖЕННОСТЬ при збільшенні темпу приросту робочої сили. У цьому випадку крива sf (k) не змінює свого положення, а нахил прямої (р + n) k росте. В результаті капиталовооруженность нового стаціонарного стану зменшується (див. Рис. 19.5). Валовий випуск зростає в новому стаціонарному стані швидше (так як темп його зростання визначається тільки темпом зростання робочої сили), але на душу населення економіка стала біднішою.

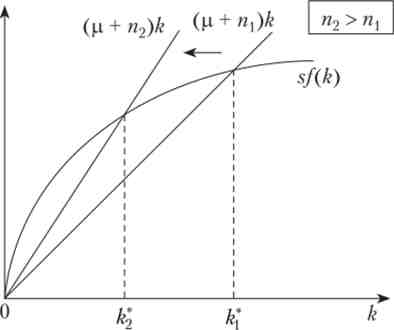
Мал. 19.5. Модель Солоу: збільшення темпу приросту населення

1. Цикли з позиції гіпотези ефективного ринку
   У 1970-х рр. гіпотеза ефективного ринку багато в чому служила концептуальною основою традиційної теорії фінансів. В даний час вона виступає в якості відправної точки для аналізу циклів в сучасній як кейнсіанської, так і класичної економічної школи. Центральні ідеї гіпотези: ринок добре регулюється
2. Циклічність
   В результаті вивчення глави студент повинен: знати основні підходи до дослідження циклічних процесів в економіці; особливості взаємодії мультиплікатора і акселератора в різних макроекономічних умовах; методи моделювання монетарних чинників циклічності; теоретичні основи імовірнісних моделей
3. Тривалість руху до динамічної рівноваги
   Відповідно до моделі Солоу - Свана при відсутності технічного прогресу або екзогенному трудосберегающих технічному прогресі економіка, яка не перебуває в стані динамічної рівноваги, обов'язково прийде до нього через певний час. В якому стані частіше знаходиться економіка, залежить від тривалості
4. Теорії мультиплікатора, мультиплікатор збалансованого бюджету
   Мультиплікатор збалансованого бюджету (M GT ) - це відношення приросту рівноважного доходу до викликав це збільшення рівному приросту автономних держвидатків і автономних податкових надходжень. Найпростіший випадок. держвидатки (G ) і податкові надходження автономні (Т а ), Інвестиції та
5. Теорія портфеля: загальний випадок
   Розглянемо моделі інвестиційного портфеля з будь-якою кількістю видів акцій. Модель 1. Розглядається задача мінімізації ризику портфеля (s 2 ) Без урахування його прибутковості. Обмеження на компоненти портфеля мають вигляд Дане завдання квадратичного програмування має два види рішень: внутрішнє
6. Теорія грошей
   Гроші не відразу з'явилися в історії людства. Природа грошей при всій простоті досить складна і неоднозначна. Щоб гроші стали грошима, потрібні були століття і тисячоліття еволюції обміну, виробництва і самого суспільства. Гроші мають переваги перед іншими формами організації взаємодії людей.
7. Теоретичне обґрунтування зв'язку розвитку населення і кредиту
   Майже повсюдно нарощування кредитних комунікацій відбувалося під впливом зростання населення. Однак висхідний тренд кредиту періодично переривався і тимчасово відступав. Як тільки намічалося скорочення приросту і, тим більше, відбувалося падіння чисельності і щільності населення, кредитні
8. Таблиці «галузь на галузь»
   Так само як для складання матриці «продукт на продукт» використовуються два методу, існують і два способи складання матриці «галузь на галузь»: 1) використання постійної структури продажів для продуктів, що передбачає залежність розподілу попиту між споживачами від продукту, а не від галузі